1. James Joule va fer una famosa sèrie d'experiments. A la figura 1 es pot veure la representació esquemàtica d'un. Feia caure un bloc de 58 lliures fins que caigués 5 peus. La caiguda accionava unes paletes que agitaven una lliura d'aigua (molt ben aïllada). L'aigua frenava la caiguda del bloc, que era pràcticament uniforme. Va comprovar que repetint la caiguda 8 vegades (equival a una caiguda de 40 peus), la temperatura de l'aigua augmentava 2,7 ºF.
a) Detalla qui fa el treball que dóna energia al sistema i quines transferències d'energia hi ha al llarg de l'experiment.
Qui aixeca el pes...
b) Calcula la disminució d'energia potencial del bloc (en les 8 caigudes) en joules, i l'augment d'energia interna de l'aigua en calories (una caloria és l'energia necessària per a augmentar 1 ºC la temperatura d'un gram d'aigua ).3,15×103 J; 680 cal.
c) Troba l'equivalència d'una caloria en joule (òbviament, aquesta unitat no existia en aquella època) a partir d'aquest experiment i compara'l amb el valor que s'accepta actualment.
1 cal = 4,62 J. És un 10% superior al valor acceptat avui.
2. A la figura 2 es
veu una nena jugant amb un saltador en tres moments diferents del salt. En el
punt A la molla té la seva extensió original,
en el punt B és quan té la màxima
compressió i en el punt C la nena està en
el punt més alt del salt. El conjunt nena+saltador
té una massa de 30
kg.
a) Indica quines formes d'energia intervenen i quines formes d'energia augmenten i quines disminueixen entre B i C.
Cinètica (primer augmenta i després disminueix, al final queda igual), potencial elàstica (disminueix), potencial gravitatòria (augmenta).
b) Si consideres que entre B i C no ha variat l'energia mecànica total del sistema, troba el valor de la constant elàstica de la molla (suposa que compleix la llei de Hooke) .
58,8×103 N/m.
c) Si després de la posició C passa a la A (sense variar l'energia mecànica), quina velocitat tindrà la nena en el moment de tocar el terra (A)? És aquesta la velocitat màxima de tot el moviment?
1,98 m/s (cap avall). No, encara augmenta mentre el pes sigui més gran que la força elàstica (k x) cap amunt, però això passarà només mig centímetre per sota d'aquesta posició i la diferència serà molt petita.
3. Si busqueu a internet "catapulta humana" trobareu uns quants vídeos amb imatges com les que es pot veure a la imatge 3. Podeu visualitzar-ne a
Es veu un home que estava a una llitera subjecta a dues gomes elàstiques tensades que són alliberades de manera que l'home surt disparat cap amunt.
Es tracta d'enviar l'home tan amunt com sigui possible (porta
un petit paracaigudes que obre a la baixada). Considerarem negligibles les masses
de la llitera i de les gomes.
a) Troba l'expressió que ens permet calcular l'altura màxima (h) en funció de la constant elàstica del dispositiu (k), de la massa del saltador (m), de l'allargament de les gomes (x) i de la gravetat (g) .
.
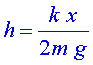b) Indica quin efecte tindrà sobre l'altura duplicar cadascuna de les següents variables indicades a l'apartat anterior (k, m, x).
Duplicar k
altura × 2; duplicar m
4. A la figura 4 es mostra un pèndol de Newton fet de 5 boles d'acer. La distància del centre de les boles al punt d'on pengen els fils és de 15 cm i hem separat el primer fil fins a 30º de la vertical. Quan deixem anar la bola alçada, baixarà fins impactar amb les boles en repòs i, tot seguit, la bola de l'altre extrem iniciarà el seu moviment.
a) Descriu les transferències i les transformacions d'energia que hi ha en el procés fins que la bola de l'esquerra arribi a l'extrem del seu moviment.
Transformació Ep
Ec; transferència E de cada bola a la següent; Ec
El procés es repeteix moltes vegades i es reprodueix gairebé igual; però un estudiant amb molta paciència observa que després de 400 "anades i tornades" l'alçada a la qual arriben les boles dels extrems s'ha reduït a la meitat.
b) Calcula l'energia mecànica que s'ha perdut en tot aquest temps.
4,43 mJ .
c) Si aquesta energia s'ha utilitzat en augmentar igual la temperatura de les 5 boles, calcula aquest increment de temperatura.
4,3x10-5ºK (indetectable!).
5. És ple estiu i tenim les begudes a fora de la nevera. En un vas tenim 300 g de refresc (essencialment aigua) a 26 ºC i hi posem un parell de glaçons de 25 g cadascun a 0ºC.
a) Calcula l'energia que absorbiran els glaçons en fondre's i la baixada de temperatura del refresc deguda només a la fusió del gel.
16,7 kJ; 13 ºC.
b) Troba la temperatura final del conjunt refresc + glaçons fosos quan s'arribi a l'equilibri tèrmic. Suposa que podem negligir els intercanvis de calor amb l'ambient.
11 ºC.
6. Hem enregistrat amb un sensor de posició l'altura d'una pilota de bàsquet (m = 600 g) mentre botava. Les distàncies es compten des del sensor que estava per sobre de la pilota que botava. En la figura 5 podeu observar la gràfica obtinguda.
a) En quines fases del moviment hi ha una pèrdua significativa de l'energia mecànica?
Cada vegada que la pilota toca el terra (fins que el torna a deixar).
b) Quin percentatge de l'energia mecànica es dissipa en el segon i en el tercer bots?
31%; 29%.
7. A casa d'un amic
tenen una "cinta de caminar" com la de la figura 6. És una
màquina per fer exercici dins de casa, amb un motor elèctric que
fa moure una cinta a velocitat constant. La velocitat es pot graduar fàcilment
i d'aquesta manera podem triar la intensitat de l'exercici. Esteu interessats
a saber quanta energia consumeix i amb un wattímetre mesureu la potència
elèctrica consumida en diferents situacions.
Els gràfics de la figura 7 mostren el consum elèctric a diferents
velocitats. La línia inferior s'ha obtingut mesurant la potència
amb la cinta funcionant sense ningú a sobre, i la línia inferior
amb una persona caminant-hi.
a) Escriu les equacions que donen la potència en funció de la velocitat a partir de les dades del gràfic. Amb les dades disponibles, de quines variables depèn l'energia consumida per la màquina?
P = 52 N × v ; P = 127 N × v.
b) Suposa que tota l'energia elèctrica s'inverteix en treball mecànic per moure la cinta. Calcula la força que fa el motor sobre la cinta en cada cas. Depèn de la velocitat? Depèn de si hi ha algú que hi camina o no?
52 N (en buit); 127 N (amb la persona caminant). No. Sí.
La màquina també ens indica quanta energia "hem cremat" amb l'exercici. Hem estat caminant a 5,4 km/h durant 20 minuts i ens indica 100 kcal.
c) Compara la potència de la màquina i la del caminador a 5,4 km/h .
Pmàq = 190 W; Ppers = 349 W.
c) Si la potència "de consum energètic" de la persona és més gran que la potència elèctrica de la màquina, podem dir que el rendiment de la cinta és de més del 100% ?
No, perquè...
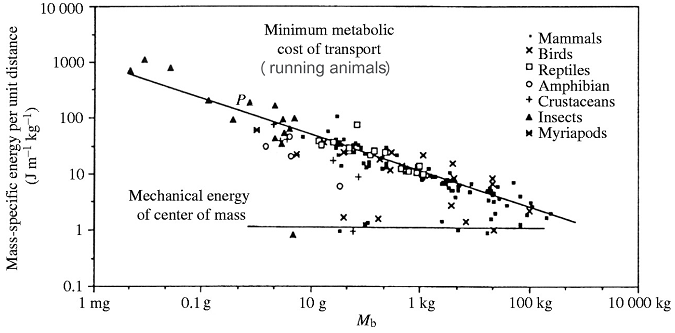
8. En un article (http://jeb.biologists.org/content/208/9/1645) trobat al Journal of Experimental Biology ("Models and the scaling of energy costs for locomotion" d'R. McNeill Alexander) han comparat el cost energètic del desplaçament d'animals de mides i sistemes de locomoció molt diversos. Aquest gràfic de la figura 8 en presenta alguns resultats: a les ordenades es representa l'energia consumida per cada quilogram (d'animal) i per cada metre de desplaçament, i a les abscisses, la massa dels animals.
Nota: on diu Mechanical energy vol dir Mechanical cost (energia mecànica necessària per avançar cada metre).
a) Observa que tant l'eix d'ordenades com l'eix d'abscisses no tenen una escala lineal sinó logarítmica. Explica el significat d'això i la conveniència d'utilitzar aquesta escala en aquest estudi.
Les magnituds estudiades s'estenen al llarg de molts ordres de magnitud i, a més, la relació obtinguda d'aquesta manera s'ajusta bé a una línia recta.
b) Quins són els animals que tenen una eficiència energètica (cost mecànic/cost metabòlic) major?
Els que tenen una massa més gran (de tota manera, és evident que per a animals que tenen una massa encara més gran, l’eficiència ja no pot augmentar més!).
c) On situaries aproximadament els humans? Fes-ne una estimació de l'eficiència.
Fig. 11:
Entre el 12% i el 35% (no sabem si els humans corresponem a un dels 2 punts que apareixen a la "nostra" zona de massa, o bé si hem d'utilitzar la línia de regressió).
9. Ens proposen aquesta màquina de produir energia (imatge 9). Només necessita una bola de fusta, un dipòsit d'aigua i uns pocs elements senzills més. La bola comença al fons del dipòsit, l'empenyiment la fa pujar, un dispositiu l'empeny horitzontalment (no cal treball) i aleshores, a l'aire, cau. Finalment una rampa la dirigeix cap a una vàlvula que deixa entrar la bola al fons del dipòsit sense que l'aigua en surti. El procés es pot repetir indefinidament i la bola pot fer treball sobre altres objectes tant a la pujada com a la baixada.
Lamentablement, aquests dispositius mai funcionen.
a) Quina llei fonamental de la física es violaria si aquesta màquina funcionés com es proposa?
Es violaria el principi de conservació de l'energia.
b) En quin punt hem d'aportar energia al sistema perquè funcioni?En reintroduir la bola a través de la vàlvula. Cal fer força contra la pressió de l'aigua.
10. Un dels problemes de l'energia elèctrica és la dificultat d'emmagatzemar-la. Les centrals hidràuliques reversibles (vegeu la figura 10) permeten emmagatzemar grans quantitats d'energia. Consten de 2 embassaments situats a diferent altura. Uns generadors permeten transformar l'energia potencial gravitatòria de l'aigua en energia elèctrica quan l'aigua passa de l'embassament superior a l'inferior, com a qualsevol central hidràulica, quan hi ha demanda de corrent. Uns motors permeten pujar l'aigua des de l'embassament inferior al superior, convertint l'energia elèctrica en energia potencial gravitatòria, quan hi ha poca demanda d'energia elèctrica. Tant els generadors com els motors desprenen quantitats importants de calor.
a) Funcionaria indefinidament el sistema si l'energia de la central tèrmica s'enviés a la xarxa elèctrica?
No (conservació de l'energia).
b) Funcionaria indefinidament el sistema si l'energia de la central tèrmica s'utilitzés també per alimentar els motors de bombament d'aigua cap amunt?
No (degradació de l'energia).
11. El llibre How bad are bananas, de Mike Berneers-Lee, analitza, calcula i compara la petjada ecològica (en producció de CO2) d'una multitud de productes i serveis, des dels plàtans fins a una guerra. Teniu aquí un fragment dedicat als vols intercontinentals:
En una font independent hem trobat que la calor de combustió del querosè d'aviació és de 42,8 MJ/kg .a) Quanta energia fa falta per transportar una persona de Londres a Hong Kong (amb les dades de l'article). Compara-la amb la despesa energètica d'un home jove amb activitat moderada (3.000 kcal/dia) .
1,19 × 1010J (2,6 anys de despesa energètica humana).
b) Quanta energia obtenim per cada tona de CO2 produït?
1,42 × 1010J ; 7,51× 1010J si tenim en compte l'impacte extra per emetre el CO2 a gran altura.
c) Compara la reducció de consum energètic de diferents opcions: millorar el control aeri, augmentar el nombre de passatgers per avió...
Resposta oberta.
d) El text parla de la dificultat d'utilitzar tecnologies no basades en els combustibles fòssils per a l'aviació. Analitzeu aquesta afirmació.
Resposta oberta. Pot parlar-se, per exemple, de l'avió solar que ha fet recentment la volta al món i veure'n les limitacions quant acapacitat i velocitat.
e) Podries proposar altres exemples de situacions en les quals ens fixem en detalls de poca importància mentre ignorem qüestions de gran impacte?
Resposta oberta. Es pot incidir en la necessitat d'acompanyar les comparacions amb càlculs o, com a mínim, estimacions quantitatives.
Autor d'aquesta pągina: Octavi Plana, professor de Física i Química a l’IES Icària de Barcelona
Aquesta
obra estą subjecta a una
Llicčncia
de Creative Commons
