La primera força variable que comença a treballar l'alumnat de secundària és la força elàstica. Presentem una activitat contextualitzada en un salt de pont ( en castellà conegut amb el nom de  puenting i en anglès amb el de  bungee jumping) que consta de tres parts. En primer lloc, estudiem l’elasticitat d’una corda dissenyant experiments per comprovar les hipòtesis de l'alumnat sobre les variables de les quals pot dependre l’elasticitat d’una corda mitjançant l’ús d’un model senzill. En segon lloc, proposem una anàlisi d’un model de salt amb l’ajuda de sensors o d’una gravació de vídeo. Aquesta anàlisi permet estudiar la seguretat en un salt de bungee. Finalment, es proposa un exercici d’aplicació.
Aquesta activitat ha estat dissenyada com a exemple de bona pràctica d’utilització de TIC dins del projecte DIATIC del Centre de Recerca per a l'Educació Científica i Matemàtica (CRECIM), de la UAB.
L’origen d’aquesta activitat és la proposta dels materials de Física en Context del Centre d'Experimentació en Ciències (CDEC) que professorat de Física de diferents instituts de Catalunya ha elaborat, experimentat i modificat, a partir del projecte Salters Horners anglès. Actualment, aquest projecte s'adapta perfectament al currículum oficial de la matèria de Física del batxillerat i està disponible lliurement en format paper i també en format digital, a l'adreça: https://sites.google.com/a/xtec.cat/fisicaencontext/

Guia per al professorat

Temporització i nivell proposat

La durada prevista d’aquesta activitat és de 4 hores, aproximadament una hora per a cada apartat.

Està dirigida principalment a primer de batxillerat, però també es pot treballar a quart d’ESO, amb una metodologia més guiada.

Orientacions

És important que l'alumnat faci hipòtesis i prediccions del que n'espera obtenir. Els canvis conceptuals són possibles si treballen sobre les seves idees inicials.

L'alumnat hauria de conèixer la llei de Hooke i l’energia elàstica.

Proposta de treball a l'aula

Primerament es dóna a l'alumnat un model de saltador i se’ls proposa que facin hipòtesis sobre les variables de les quals pot dependre l’elasticitat d’una corda.

A continuació se’ls demana que dissenyin possibles experiments per comprovar les seves hipòtesis a partir de la comparació de les constants d'elasticitat calculades.

Una vegada que han trobat de què depèn l’elasticitat d’una corda, fan un experiment amb diferents saltadors i una determinada corda d’una longitud concreta per determinar mitjançant un full de càlcul el valor de la constant d’elasticitat amb la qual treballaran posteriorment.
En la segona part, han d’analitzar un salt del model de saltador. Es pot fer amb un sensor de distància o amb l’enregistrament d’un vídeo del salt del model de saltador per fer-ne una anàlisi després. Prèviament es demana a l'alumnat que faci una predicció dels gràfics posició-temps, velocitat-temps i acceleració-temps.
A continuació han d'analitzar els punts més significatius del moviment i els trams que hi ha entre ells de les gràfiques que han obtingut interpretant diverses magnituds cinemàtiques, dinàmiques i energètiques, per poder respondre si el salt del model és o no és segur i emocionant.
Finalment, es proposa un exercici numèric aplicable a la situació real del context.

Material

Un model de saltador (figura 1): el que hem fet servir és de i ha estat dissenyat amb un rodet de fotos amb dos forats en la superfície lateral pels quals farem passar un filferro al qual lligarem una goma elàstica de del núm. 1. Diferents gomes elàstiques (de diferents números i gruixos) de diferents llargades. La que s’ha utilitzat per a la segona part ha estat de del núm. 1, encara que varia la constant d’elasticitat amb la marca. En aquest cas . Saltadors de diferents masses (es poden afegir boles, plastilina... a l’interior del rodet de fotos). Regle o cinta mètrica. Dinamòmetre o sensor de força. Sensor de posició. El que hem utilitzat és de la marca , perquè el de Multilog, que és més utilitzat en els centres no permet detectar tan bé un model de saltador tan petit. Gravació de vídeo, si no es disposa d’un sensor de distància adient.

Fig. 1: Model de saltador

Full de l'alumnat

Introducció

Amb la crisi que ens afecta, un grup d’amics hem decidit crear una empresa d’esports d’aventura i com que el pare d’un de nosaltres té una grua que ja no fa servir hem pensat utilitzar-la per fer salts de pont o bungee jumping.

Com podem aconseguir un salt emocionant i segur?

Primerament simularem un salt amb un model de laboratori i valorarem els límits d’aquest model.

De què depèn l’elasticitat d’una corda?

Material

• Cordes elàstiques de diferent naturalesa (diferents gruixos).
  
• Dinamòmetres o sensors de força.
  
• Regle.
  
• Model de saltador amb diferents masses.

El primer que heu d’investigar és com són les cordes que s’utilitzen en aquests salts.

Quines característiques penseu que han de tenir aquestes cordes?

Podem suposar que aquestes cordes segueixen la llei de Hooke (la força elàstica o força recuperadora d’una corda elàstica és proporcional a l’allargament de la mateixa) per als allargaments que es produeixen en el salt.

Volem fer una anàlisi més profunda de les variables de les què depenen aquestes cordes.

De què creieu que depèn l’elasticitat d’una corda?

Comprovem-ho amb una corda elàstica i un model de saltador.

Mesurarem l’elasticitat d’una corda a partir de la seva constant d’elasticitat.

Què podríeu fer per investigar si l’elasticitat depèn de cadascuna de les variables que heu suposat?

Dissenyeu possibles experiments en els quals comproveu les vostres hipòtesis sobre l’elasticitat d’una corda. Penseu que heu de triar cadascuna d’aquestes variables i fixar les altres.

Resumiu el que fareu en aquesta taula:

Primerament, estudiem si l’elasticitat depèn de la longitud de la corda.

Com són els valors de la constant d’elasticitat que heu obtingut?

Ara feu el mateix per a dues cordes de diferent naturalesa.

Com són ara els valors de la constant d’elasticitat?

Com podríeu aconseguir una corda de diferent naturalesa si només teniu un tipus de corda?

I, finalment, feu el mateix per a dos saltadors de diferent massa.

Com són en aquest cas els valors de la constant d’elasticitat que heu obtingut?

Resumint, de quines variables depèn l’elasticitat d’una corda?

Com que els saltadors del projecte que estem dissenyant seran diferents, hem de trobar el valor de la constant d’elasticitat de la corda que farem servir, a partir de la llei de Hooke.
Trieu un tipus de corda d’una longitud concreta. En el nostre cas, una corda del núm. 1 de .

Trobeu el valor de la constant d’elasticitat en aquest cas utilitzant un full de càlcul a partir del gràfic força elàstica-allargament de la corda.

Quins són els moments més emocionants del salt?

Material

• Sensor de posició o vídeo d’un model de salt de piont.
  
• Programa d’anàlisi de dades del sensor o del vídeo tipus o .
  
• Model de saltador ().
  
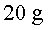• Corda utilitzada en l’últim experiment (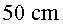del núm. 1).

Feu diferents diagrames de les forces que actuen sobre el saltador al llarg del salt.

Intenteu predir quins són els punts del salt on hi ha un canvi en la velocitat, l'acceleració, les forces sobre el saltador, els diferents tipus d'energia...

Feu una predicció qualitativa dels gràfics posició-temps, velocitat-temps i acceleració-temps del saltador que creieu que obtindreu.

Fig. 2: Gràfic posició-temps

Fig. 3: Gràfic velocitat-temps

Fig. 4: Gràfic acceleració-temps

Feu servir un programa d’anàlisi de vídeos (Multilab o LabQuest) per obtenir el gràfic posició-temps.
A partir d’aquest gràfic, trobeu els gràfics velocitat-temps i acceleració-temps.

Quants punts i trams es poden diferenciar en el salt? Assenyaleu aquests punts en els gràfics anteriors. Fixeu-vos només en el primer bot, fins que arriba a baix.

Compareu els gràfics que heu trobat amb els de les prediccions que havíeu pensat.

Es compleixen les mesures de seguretat?

En aquest apartat analitzarem els gràfics obtinguts.

En quin moment s’assoleix la màxima acceleració en el salt de pont que esteu estudiant?

Hem de tenir en compte segons la legislació vigent unes mesures de seguretat.

Una persona és capaç de suportar una acceleració de fins a . A partir d’aquest valor pot perdre el coneixement, trencar-se algun lligament i patir altres problemes de salut. L’acceleració límit que suporta com a màxim una persona que va a una atracció com l’Hurakan Condor és 3 vegades la gravetat (), encara que els conductors de fórmula 1 arriben a acceleracions superiors.

El vostre model compleix les mesures de seguretat legals perquè el saltador no tingui problemes de salut? Què podríeu fer si no es compleixen les mesures de seguretat? En el salt de pont de les atraccions (vegeu la figura 4), quina diferència hi ha entre les cordes que es fan servir amb un nen i amb una persona adulta? També és emocionant la velocitat que s’arriba a assolir en un salt de pont. En quin moment s’assoleix la màxima velocitat? Feu un resum qualitatiu en la taula de les variables dinàmiques que caracteritzen aquests trams (velocitat, acceleració, forces que actuen sobre el cos i força resultant) i digueu cap a on actuen, si augmenten o disminueixen i el seu sentit en cada cas. La taula la trobareu al final del protocol de l’activitat.

Fig. 5: Gràfic acceleració-temps

Des de quina alçada podem deixar caure el nostre saltador perquè el salt sigui emocionant, és a dir, arribi just per sobre del terra?

En aquest apartat farem un estudi energètic del salt per poder completar la resposta una de les preguntes inicials que ens havíem plantejat. Suposarem que no hi ha dissipació d’energia.

Perquè el vostre saltador quedi a per sobre del terra, des de quina alçada hauria de caure? Comproveu-ho amb el vostre model de saltador.

A la vista del que heu treballat en aquest apartat, feu un resum energètic en la taula següent en els punts i trams que heu considerat anteriorment.

Punt o tram	Velocitat (zero, augmenta, disminueix, constant, màxima, mínima)	Acceleració (zero, augmenta, disminueix, constant, màxima, mínima)	Forces (compareu les intensitats de les forces)	Energia cinètica (zero, augmenta, disminueix, constant, màx., mín.)	Energia potencial gravitatòria (zero, augmenta, disminueix, constant, màx., mín.)	Energia potencial elàstica (zero, augmenta, disminueix, constant, màx., mín.)	Energia mecànica (zero, augmenta, disminueix, constant, màx., mín.)
A
A-B
B
B-C
C
C-D
D

Aplicació

Aquest diumenge voleu comprovar si la recerca que heu fet és vàlida en el vostre cas.
Suposeu que disposeu d’una corda de de longitud i voleu saltar des d’una altura de .
El primer que fareu és saber si la corda és l’adequada.
La persona que saltarà, que té una massa de , es penja de la corda i comprova que s’allarga en el punt l’equilibri.

Si el saltador es deixa caure sense cap velocitat inicial, és prudent utilitzar aquesta corda per saltar des del pont indicat? Per respondre la pregunta feu una estimació de la longitud màxima que tindrà la corda quan es deixi caure el saltador i recordeu de no tenir en compte la resistència amb l’aire.
On s’assoleix la velocitat màxima? Calculeu-la i expresseu el resultat en km/h.
A quina acceleració màxima arribarà el saltador? Afecta la seva salut?
Quina és la força màxima que ha de suportar l’enganxament de la corda amb el pont?

Per seguretat es decideix utilitzar dues cordes iguals en paral·lel.

Quina longitud màxima arribaran a tenir les dues cordes?
Quina serà l’acceleració màxima de la persona que salta en aquestes condicions?
Serà convenient utilitzar una corda doble per realitzar un salt més segur?

Solucions

Quines característiques penseu que han de tenir aquestes cordes?
Les cordes han de ser elàstiques perquè el temps de frenada sigui el més llarg possible, per tal que disminueixin l’acceleració i la força sobre el saltador en el moment del bot.

De què creieu que depèn l’elasticitat d’una corda?

Hipòtesis possibles:

• De la longitud de la corda.
  
• De la naturalesa de la corda (més o menys gruixuda).
  
• De la massa del cos que s’hi pengi.
  

Què podríeu fer per investigar si l’elasticitat depèn de cadascuna de les variables que heu suposat?
Variar cadascuna de les magnituds proposades i mantenir constants les altres.

Dissenyeu possibles experiments en els quals comproveu les vostres hipòtesis sobre l’elasticitat d’una corda. Penseu que heu de triar cadascuna d’aquestes variables i fixar-ne les altres.
L’elasticitat la trobarem a partir de la constant d’elasticitat de la goma elàstica. Per trobar , es pot fer servir un dinamòmetre o un sensor de força.
És important que els alumnes s’adonin que treballarem en el punt d’equilibri de l’estirament de la corda en tots aquests experiments (mòdul del pes igual al mòdul de la força elàstica). En aquest punt, el pes i la força que fa la corda sobre el cos tenen el mateix mòdul.
Dependència de la longitud de la corda: dues cordes de la mateixa naturalesa i diferent longitud de les quals pengen dos cossos de massa diferent
Dependència de la naturalesa de la corda (més o menys gruixuda): dues cordes de diferent naturalesa, la mateixa longitud i la mateixa massa que el saltador.
Dependència de la massa del cos que es penja: una corda en la qual variarem la massa del cos que en penja
En els dos primers cassos, varia. En el tercer cas no.

Resumiu el que fareu en aquesta taula:

Com són els valors de la constant d’elasticitat que heu obtingut?
Diferents valors de per a diferents longituds de la corda.

Com són ara els valors de la constant d’elasticitat?
Diferents valors de .

Com podríeu aconseguir una corda de diferent naturalesa si només teniu un tipus de corda?
Doblant-la. Aquesta és la solució si només tenim un tipus de corda.

Com són en aquest cas els valors de la constant d’elasticitat que heu obtingut?
Els mateixos valors de .

Resumint, de quines variables depèn l’elasticitat d’una corda?
De la naturalesa i de la longitud de la corda.

Trobeu el valor de la constant d’elasticitat en aquest cas utilitzant un full de càlcul a partir del gràfic força elàstica - allargament de la corda.
Hem de suposar que en el tram en el qual treballem la constant d’elasticitat és constant; per tant, hem d’ajustar a una línea de tendència lineal els punts força elàstica-allargament de la corda que representem per trobar a partir del pendent el valor de la constant elàstica. En el nostre cas hem trobat: .

Quins són els moments més emocionants del salt?

Feu diferents diagrames de les forces que actuen sobre el saltador al llarg del seu salt.
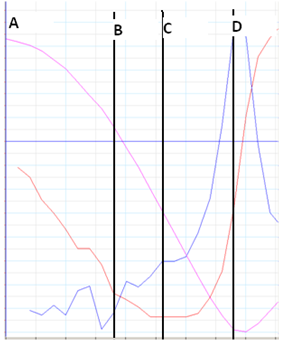
Sobre un esquema de saltador s'han de tenir en compte diferents moments:

• Entre la sortida (A) i quan comença a estirar-se la corda (B): només actua la força de la gravetat.
  
• Entre el punt B i el punt de bot (D), màxim allargament actuen dues forces: la força de la gravetat i la força elàstica de la corda.
  
• Com que la força elàstica augmenta amb l’allargament de la corda, arriba un moment en què la força elàstica és igual al pes (C) i a partir d’aquest punt és superior la força elàstica.
  

Intenteu predir quins són els punts del salt on hi ha un canvi en la velocitat, l'acceleració, les forces sobre el saltador, els diferents tipus d'energia...
Es poden considerar els següents punts i intervals importants:

• El punt de sortida A.
  
• El tram A-B.
  
• El punt B, punt on la corda comença a estirar-se.
  
• Tram B-C.
  
• Punt C, punt d’equilibri, on la velocitat és màxima.
  
• Tram C-D.
  
• Punt D, punt més baix on arriba el saltador, on la corda està estirada al màxim, la velocitat és nul•la i l’acceleració és màxima.
  

Feu una predicció qualitativa dels gràfics posició-temps, velocitat-temps i acceleració-temps del saltador que creieu que obtindreu..
Cada alumne farà la seva predicció.

Quants punts i trams es poden diferenciar en el salt? Assenyaleu aquests punts en els gràfics anteriors. Fixeu-vos només en el primer bot, fins que arriba a baix.

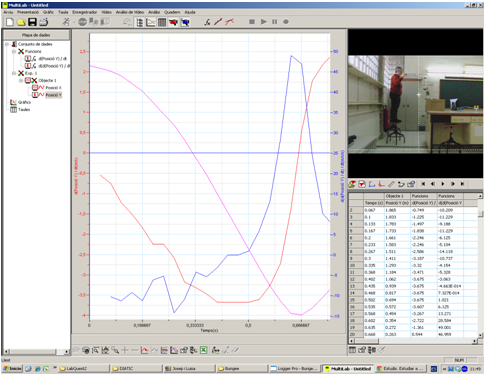
Obtindrem uns gràfics com aquests (vegeu les figures 6 i 7 si hem treballat amb un vídeo: càmera ràpida i una freqüència de 30 fotogrames per segon), mitjançant l’anàlisi amb el programa Multilab. Haurem de fer servir l’eina derivada de la gràfica posició y – temps i derivada de la gràfica anterior, per obtenir els gràfics , i
És interessant que els alumnes distingeixin els quatres punts més significatius i vegin les característiques de cadascun (posició, velocitat i acceleració).
El gràfic de color rosa és el de posició-temps, el vermell de velocitat-temps i el blau d’acceleració-temps.

Fig. 6:

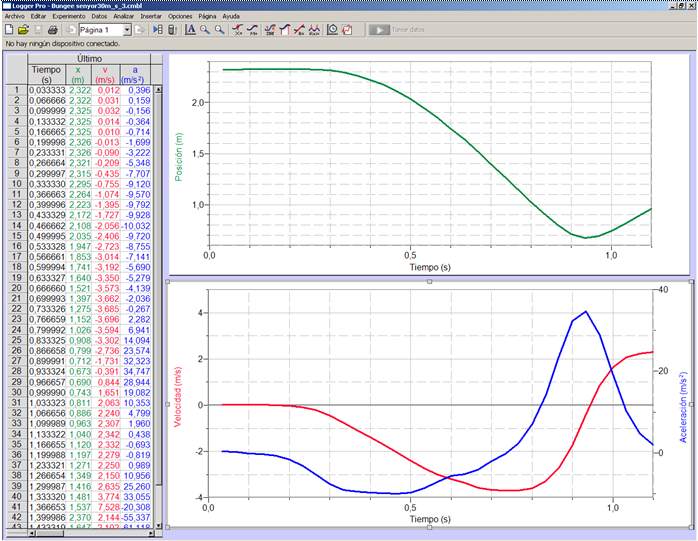
Fig. 7:

Si treballeu amb un sensor Vernier de distància per crear els gràfics, podeu arribar a obtenir els gràfics següents (vegeu la figura 8).
El gràfic verd és el de posició-temps, el vermell de velocitat-temps i el blau d’acceleració-temps.

Fig. 8:

Compareu els gràfics que heu trobat amb els de les prediccions que havíeu pensat.
Cada alumne fa la comparació en funció de les seves prediccions.

Es compleixen les mesures de seguretat?

En quin moment s’assoleix la màxima acceleració en el salt de bungee que esteu estudiant?
En el punt més baix, en el bot.

El vostre model compleix les mesures de seguretat legals perquè el saltador no tingui problemes de salut?
No, perquè l’acceleració és de segons podem observar el gràfic .

Què podríeu fer si no es compleixen les mesures de seguretat?
Com que l’acceleració és directament proporcional a i a l’allargament, hauríem de trobar un compromís entre variar i variar l’allargament:



En el salt de pont de les atraccions (vegeu la figura 4), quina diferència hi ha entre les cordes que es fan servir amb un nen i amb una persona adulta?
Es posen més cordes quan la persona té més pes; això fa que augmenti i l’allargament disminueixi.

En quin moment s’assoleix la velocitat màxima?
En el punt d’equilibri C, on l’acceleració és nul•la.

Feu un resum qualitatiu en la taula de les variables dinàmiques que caracteritzen aquests trams (velocitat, acceleració, forces que actuen sobre el cos i força resultant) i digueu cap a on actuen, si augmenten o disminueixen i el seu sentit en cada cas. La taula la trobareu al final del protocol de l’activitat.

Punt o tram	Velocitat (zero, augmenta, disminueix, constant, màxima, mínima)	Acceleració (zero, augmenta, disminueix, constant, màxima, mínima)	Forces (compareu les intensitats de les forces)	Energia cinètica (zero, augmenta, disminueix, constant, màxi, mín)	Energia potencial gravitatòria (zero, augmenta, disminueix, constant, màx, mín)	Energia potencial elàstica (zero, augmenta, disminueix, constant, màx, mín)	Energia mecànica (zero, augmenta, disminueix, constant, màx, mín)
A	0 mínima				màxima
A-B	Augmenta			augmenta	disminueix		constant
B							constant
B-C	augmenta	disminueix		augmenta	disminueix	augmenta	constant
C	màxima						constant
C-D	disminueix	disminueix		disminueix	disminueix	augmenta	constant
D					mínim	màxima	constant

Des de quina alçada podem deixar caure el nostre saltador perquè el salt sigui emocionant, és a dir, arribi just per sobre del terra?

Perquè el vostre saltador quedi a per sobre del terra, des de quina alçada hauria de caure? Comproveu-ho amb el vostre model de saltador.
Aquesta pregunta es pot respondre a partir del gràfic o a partir de càlculs. En aquest cas aplicarem el principi de conservació de l’energia mecànica en els punts A i D:

• Variació d’energia potencial gravitatòria + variació d’energia potencial elàstica .
• Una vegada que obtinguem la llargada de la corda amb les dades del model, hi hem de sumar de seguretat.

A la vista del que heu treballat en aquest apartat, feu un resum energètic en la taula següent en els punts i trams que heu considerat anteriorment.
Vegeu la taula anterior.

Aplicació

Si el saltador es deixa caure sense cap velocitat inicial, és prudent utilitzar aquesta corda per saltar des del pont indicat? Per respondre la pregunta, feu una estimació de la longitud màxima que tindrà la corda quan es deixi caure el saltador i recordeu de no tenir en compte la resistència amb l’aire.
Primerament hem de trobar el valor de amb les dades que ens donen:
Com que , obtenim que
Aplicant el principi de conservació de l’energia mecànica entre els punts A i D s’obté que la corda tindrà una llargada de . És més petita que , però aquesta altura és massa justa perquè sigui segura.

On s’assoleix la velocitat màxima? Calculeu-la i expresseu el resultat en.
Al punt d’equilibri C.
Aplicant el principi de conservació de l’energia entre els punts A i C
,
o btenim una velocitat de .

A quina acceleració màxima arribarà el saltador? Afecta la seva salut?
Com que l’acceleració màxima és al punt més baix D, a partir del resultat de l’apartat A . A continuació aplicant la segona llei de Newton per trobar l’acceleració en D:

El resultat és una acceleració de; per tant, no té per què perjudicar la seva salut.

Quina és la força màxima que ha de suportar l’enganxament de la corda amb el pont?
Aplicant la llei de Hooke a l’allargament del punt D, ja que aquesta és la força màxima que suportarà l’enganxament:

Quina longitud màxima arribaran a tenir les dues cordes?
Com que ara serà el doble,, obtenim una longitud de.
Quina serà l’acceleració màxima de la persona que salta en aquestes condicions?
L'acceleració serà de .
Serà convenient utilitzar una corda doble per realitzar un salt més segur?
Segons el valor de l'acceleració obtinguda, aquest salt no serà segur.

ISSN: 1988-7930 DL:  B-31773-2012   Adreça a la xarxa: www.RRFisica.cat    Adreça electrònica: redaccio@rrfisica.cat  difusio@rrfisica.cat
Comitè de redacció : Josep Ametlla, Octavi Casellas, Xavier Jaén, Gemma Montanyà, Cristina Periago, Octavi Plana, Jaume Pont i Ramon Sala.
Treballem conjuntament : Societat Catalana de Física, Associació de Professores i Professors de Física i Química de Catalunya,XTEC, Universitat Politècnica de Catalunya, Universitat de Barcelona

Recursos de Física col·labora amb la baldufa i també amb ciències Revista del Professorat de Ciències de Primària i Secundària (Edita: CRECIM-UAB)