núm 1 |
Primavera del 2008 |
Societat Catalana de Física |
| Inici |
| Sumari |   8/9 8/9  |
| Veure les línies de camp magnètic amb miniaplicacions Cristina Periago i Xavier Bohigas |
|
| En aquest article comentarem la utilització d’una miniaplicació (applet) amb la qual es poden mostrar les línies de camp magnètic creades per diferents distribucions de corrent. Aquesta miniaplicació permet representar molts camps diferents però nosaltres ens centrarem només en dos tipus de distribució de corrent molt senzills d’estudiar: el fil rectilini infinit i la bobina recta. |
IntroduccióLes línies de camp són representacions matemàtiques que ens ajuden a fer-nos una idea global del camp vectorial en una regió de l’espai. Normalment, a classe, mostrem les línies de camp amb un dibuix a la pissarra que, si no tenim gaires aptituds artístiques, sol tenir un aspecte bastant deficient. Si en volem millorar la qualitat, podem usar una transparència feta a partir d’un diagrama d’un llibre. En qualsevol cas, tenim l’inconvenient d’utilitzar imatges fixes. Si volem mostrar com varia la distribució de les línies de camp, en modificar un dels elements que constitueixen el sistema, hem de tornar a fer el dibuix o utilitzar una altra transparència. En aquest article comentarem la utilització d’una miniaplicació amb la qual es poden mostrar les línies de camp magnètic creades per diferents distribucions de corrent. A primer cop
d’ull, la miniaplicació sembla molt complicada
d'utilitzar. Té moltes finestres, cada una d’elles
amb moltes opcions, les etiquetes estan en anglès, etc. Atabala
una mica, però no ens hem d’espantar. No cal esgotar el
sistema. Únicament amb algunes de les seves opcions ja
podem obtenir resultats molt satisfactoris.
L'activitat que proposem està pensada per dur-se a terme a l'aula. És una activitat de suport per als continguts teòrics sobre al camp magnètic. Es tracta simplement de mostrar línes de camp magnètic d'alguns sistemes senzills.El nivell de dificultat dependrà dels comentaris que hi vulguem afegir. Pot ser una activitat per al segon curs de batxillertat o per al primer curs d'universitat. La duració de l'activitat dependrà també del nivell de profunditat de les explicacions i de les discussions que es generin.Creiem que al batxillerat amb uns 10 minuts n'hi ha prou.Necessitarem disposar d'una aula amb connexió a Internet i un projector. La miniaplicació que farem servir esta dissenyada per Paul Faslstad i es troba a la pàgina web http://www.falstad.com, on podeu trobar altres miniaplicacions de física d’accés lliure. També hi podeu accedir a través de: http://www.rrfisica.cat/rrfisica/fislets/h0fj026/h0fj026.htm.
ja que són les situacions que habitualment estudiem a classe. En una segona persiana, just a sota de l’anterior, podem
triar com visualitzar les línies de camp (Display: Field Lines).
Podem veure-hi altres magnituds, però aquesta és la que millor
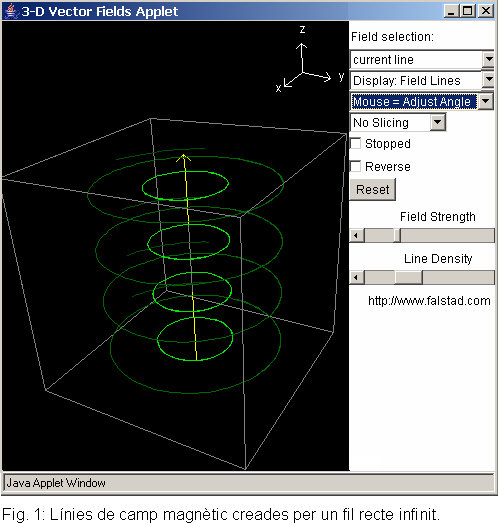
representa el camp magnètic. Camp magnètic creat per un fil rectilini infinitLa representació de les línies de camp del fil rectilini infinit (vegeu la figura 1), ens permet veure de manera ràpida i senzilla que les línies de camp són tancades (recordem que el camp magnètic és un camp solenoïdal). També podem aprofitar, si hem calculat prèviament
l’expressió analítica del camp, per veure que les línies
de camp són circumferències centrades en l’eix del fil,
i que el mòdul del camp depèn inversament de la distància
al fil. Aquesta darrera propietat la podem comprovar observant el color verd
més intens de la línia, quan la distància al fil és
menor (el color més lluminós indica un camp més intens). Camp magnètic creat per una bobina rectaLa representació de les línies de camp de la bobina recta (vegeu la figura 2) és la que té més opcions i ens permet estudiar com varia el camp magnètic en funció de la geometria, així com analitzar el rang de validesa dels resultats calculats prèviament, corresponents a l’anomenada bobina llarga. En aquest cas podem variar el nombre d’espires (#
of Turns), el seu diàmetre (Diameter) i la
longitud de la bobina (Height), i observar com es modifiquen
les línies de camp. Pot ser interessant visualitzar el camp magnètic creat per dues espires separades (loop pair stacked). Si modifiquem la distància entre les dues espires, podem analitzar com varia el camp magnètic quan aquestes estan “més separades” o “molt juntes”. Podem comparar aquestes representacions amb la de la bobina recta, cosa que ens ajudarà a comprendre que la bobina la podem considerar com un conjunt d’espires molt properes les unes a les altres.
|
|||||||||||||||||


 Quan
obrim la miniaplicació apareix una representació del camp magnètic
que apareix per defecte.
Quan
obrim la miniaplicació apareix una representació del camp magnètic
que apareix per defecte.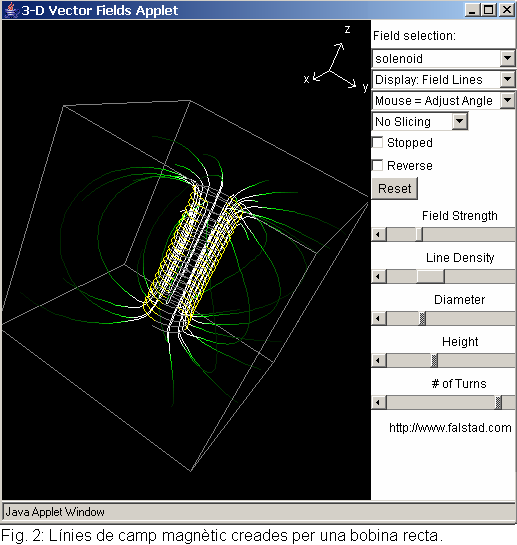 Si augmentem el nombre d’espires, veurem que les línies de camp
queden bastant ben “canalitzades” a l’interior de la bobina.
A més, si disminuïm el diàmetre de les espires podem veure
que el camp magnètic a l’interior és homogeni (les línies
de camp són rectes paral·leles a l’eix de la bobina, i el
mòdul del camp és constant) i que fora de la bobina és
pràcticament nul (en els extrems de la bobina, les línies de camp
es van separant i gairebé “desapareixen” en punts molts llunyans,
en punts exteriors, propers als costats del cilindre que constitueix la bobina,
gairebé no hi ha línies de camp).
Si augmentem el nombre d’espires, veurem que les línies de camp
queden bastant ben “canalitzades” a l’interior de la bobina.
A més, si disminuïm el diàmetre de les espires podem veure
que el camp magnètic a l’interior és homogeni (les línies
de camp són rectes paral·leles a l’eix de la bobina, i el
mòdul del camp és constant) i que fora de la bobina és
pràcticament nul (en els extrems de la bobina, les línies de camp
es van separant i gairebé “desapareixen” en punts molts llunyans,
en punts exteriors, propers als costats del cilindre que constitueix la bobina,
gairebé no hi ha línies de camp).
