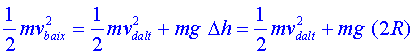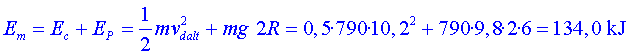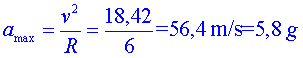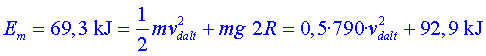núm 13 |
Primavera 2014 |
Societat Catalana de Física |
| Inici |
| Sumari |   2/8 2/8  |
| El cas de fer el bucle Lorenzo Ramírez |
|
| Es proposa una activitat en què els alumnes treballen sobre un vídeo real, d'un cotxe fent un bucle, i mesuren magnituds físiques rellevants. |
Guia per al professoratIntroducció
Hi ha bàsicament quatre maneres d’obtenir dades experimentals en les situacions que utilitza el professorat per estudiar la mecànica. La primera es basa en el regle i el cronòmetre;la segona, en l’ús de sensors connectats a un ordinador (Multilog i similars);la tercera, en l’anàlisi de filmacions, i la quarta, més recent, en l’aprofitament dels sensors que inclouen els nous telèfons intel•ligents i tauletes. Per a aquest últim cas, vegeu l’article de Tavi Casellas en el número 12 de la revista Recursos de Física i/o una entrada en el blog de l'autor d'aquest article: La tercera proposta experimental que s’indica normalment
s’ha utilitzat analitzant vídeos de moviments realitzats en condicions
controlades i filmats pel mateix professorat, pels seus alumnes o per un col•lega
que ha penjat el vídeo a Internet. Per exemple: un baló que es
deixa caure, un pèndol que oscil•la, etc.
|
 |
| Fig 2: |
Un dels problemes típics de llapis i paper de la mecànica a les classes de Física al batxillerat és el del càlcul de les condicions en les quals un objecte (bola, cotxe...) pot realitzar un tomb verticalment. Un exemple d’enunciat tancat seria el següent:
Un cotxet de joguina que té100 g de massa és llançat a 20 m/s per un carril sense fregament que és inicialment horitzontal i després té un bucle que té un radi d'1,5 m.
a. Quina velocitat té a la part alta del bucle?
b. Quina força rep el carril a dalt del tot? Quina força fa el carril sobre el cotxet en aquest mateix punt?
c. Amb quina celeritat mínima s’hauria de llançar el cotxet perquè superés el bucle?
 |
| Fig 2: |
Una alternativa o un complement a la resolució d’aquest problema és fer l’estudi amb una pista de la joguina de cotxes Hot Wheels:
És possible comprar, per menys de 20 €, la joguina
en la qual els cotxes fan el bucle i estudiar-ne el moviment per qualsevol dels
mètodes experimentals indicats en la introducció. Però,
si es disposa d’una filmació del mateix moviment amb un cotxe real
en un bucle real, pot ser que l’estudi resulti més engrescador
tant per a l’alumnat com per al mateix professorat.
Moltes vegades és difícil trobar-se amb gravacions de moviments
reals (cotxes que xoquen, objectes que cauen, pilotes que volen, etc.) que estiguin
filmades amb la perspectiva i l’angle adequats per estudiar-los i que,
a més, es puguin aprofitar per treballar a classe. El professor Vicente
Torres, que escriu el blog El Tao de la Física, en té
recollides algunes:
No és el cas del bucle, ja que hi ha diverses gravacions fetes amb motiu de la consecució de diversos rècords mundials:
Vídeo de Fifth Gear TV pel rècord de la casa Dunlop el 2009
Automòbils xinesos Zhejiang Youngman Lotus Automobile pel rècord del 2011
Doble bucle de l’empresa Hot Wheels en els Hot Wheels Real Car Backflip X Games a Los Angeles l'any 2012
El vídeo que proposem analitzar és el primer, que es va realitzar
amb motiu d’un espectacle promocional de la casa de pneumàtics,
en el qual un cotxe utilitari feia el tomb en un bucle de 12 m de diàmetre..
Temporització
El treball proposat tindrà una durada d'unes tres o
quatre hores de classe:
Una primera sessió per ensenyar com es fa funcionar el programa de punteig
i anàlisi de vídeos Tracker
i per estudiar un moviment gravat.
Una segona sessió a l'aula per presentar la situació física
que es dóna en un looping i fer diferents problemes amb llapis i paper.
Una tercera sessió a classe o a casa en la qual l’alumnat fa autònomament
la feina.
I la darrera sessió de posada en comú.
Alumnes als quals s’adreça l’experiència
Alumnat de Física de 1r batxillerat. En el nostre cas s'ha realitzat en treballar el tema 5, Satèl•lits a l’espai, de Física en context:
Orientacions tècniques
Per analitzar els vídeos s’han de baixar prèviament
de YouTube a l’ordinador. Això no es pot fer directament perquè
YouTube no ho permet i s’ha d’utilitzar un gestor de descàrregues
compatible amb el vostre navegador o bé una pàgina web que ho
faci. La meva recomanació és que el professorat el baixi i el
torni a penjar en la intranet del centre educatiu a l’abast fàcil
de tot l’alumnat que l’hagi de fer servir.
Per analitzar els vídeos existeixen diferents programes, encara que actualment
el més recomanable és Tracker. És molt potent, fàcil
de fer anar, de codi lliure i disponible per a tots els sistemes operatius.
L’heu de descarregar i instal•lar al vostre ordinador incloent-hi
el Xuggle, que porta incorporat en el mateix instal•lador i que permet
visualitzar qualsevol tipus de format de vídeo. El programa té
un manual d’una versió anterior traduït al castellà
i hi ha també un petit manual per començar
escrit per Valentí Ferrer, professor de Física i Química
a l'Institut Salvador Dalí del Prat de Llobregat.
Algunes dades de l’espectacle de Dunlop
Va ser rècord mundial del bucle més gran que
mai s’havia fet amb un cotxe, concebut per Dunlop en col•laboració
amb FifthGear TV l’any 2009 (superat després, el 2011). Es va fer
al camp d’aviació BentwatersAirfield,a Suffolk (Regne Unit).
Es va construir una estructura circular de 12 metres de diàmetre i 4,5
tones de placa d’acer DurBar de 3 mm, sustentada en una base de formigó
de 20 tones com a llast per evitar que el bucle s’enlairés. L’amplada
de la pista era de 3 metres.
L’automòbil que va fer el bucle va ser un cotxe petit d’1,6
metres d’amplada, un Toyota Aygo 1.0 VVT, i de 68 CV, al qual van retirar
algunes peces (per reduir-ne el pes) i també la part de sota del frontal,
perquè no xoqués amb la pista corbada. A més,hi van instal•lar
reforços de seguretat estructurals. Per fer el bucle portava 3 litres
de gasolina i pneumàtics normals SP30 de Dunlop, per descomptat!
En els vídeos que recullen el bucle i la seva preparació, a més
de SteveTruglia, especialista en pel•lícules d’acció
i recordista múltiple, i que és el pilot que condueix el cotxe,
també hi surt l’enginyer i divulgador de la ciència Hugh
Hunt, de la Universitat de Cambridge, que fa l’estudi teòric previ
del moviment.
Full de l’alumnat
Introducció
En estudiar la dinàmica del moviment circular és molt habitual que el professorat us proposi resoldre situacions en les quals un objecte descriu un moviment circular en el pla vertical: una pedra lligada a una corda, una sínia, etc. En aquest cas us plantegem l’estudi d’una altra situació de moviment circular vertical agafada de la vida real.
Objectiu
Es tracta que estudieu les condicions en què un cotxe pot fer el bucle en una pista circular vertical. Per fer-ho, disposeu d’una filmació en la qual un cotxe ho aconsegueix.
Material
Ordinador
Programari de punteig de vídeo i anàlisi de dades (Tracker)
Filmació del cotxe fent el bucle en el vídeo de FifthGear TV
El professor Hugh Hunt explica la ciència del bucle
Realització/procediment
Baixeu del Moodle del vostre centre (o de YouTube) el vídeo
del rècord mundial 2009 de bucle amb un cotxe que va realitzar el canal
de televisió FifthGear TV. Per baixar-lo de YouTube necessitareu un gestor
de descàrregues compatible amb el vostre navegador.
Visioneu-lo per comprovar que es veu bé i fixeu-vos en quin interval
de la filmació hi ha la seqüència lateral del cotxe fent
el bucle.
Baixeu també el programa Tracker i instal•leu-lo al vostre ordinador
incloent-hi el Xuggle, que porta incorporat en el mateix instal•lador,
per poder visualitzar qualsevol tipus de format de vídeo.
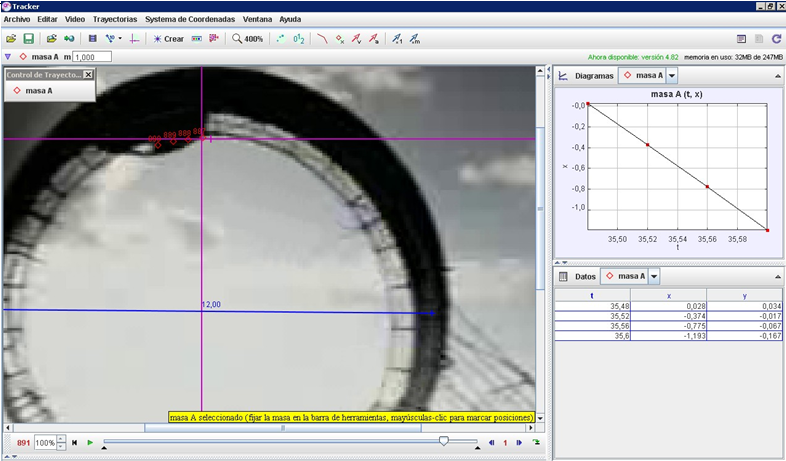
Ara ja podeu obrir el Tacker, carregar-hi el vídeo del bucle, anar a
l'instant en què es veu el cotxe fent el bucle i prendre les dades que
necessiteu. Podeu trobar aquí un petit manual del Tracker, suficient
per al vostre treball:
Activitats que s’han de realitzar
 |
| Fig 4: |
![]() Activitat 1: Calculeu teòricament la celeritat mínima
que hauria de portar el cotxe quan entra en el bucle i també en el punt
més alt, per no caure.
Activitat 1: Calculeu teòricament la celeritat mínima
que hauria de portar el cotxe quan entra en el bucle i també en el punt
més alt, per no caure.
![]() Activitat 2: Trobeu, amb l’ajut del Tracker, la rapidesa
amb la qual el cotxe entra en el llaç, la que porta quan està
vertical (un quart de volta) i la que té a dalt del tot del bucle.
Activitat 2: Trobeu, amb l’ajut del Tracker, la rapidesa
amb la qual el cotxe entra en el llaç, la que porta quan està
vertical (un quart de volta) i la que té a dalt del tot del bucle.
![]() Activitat
3: Calculeu la força extra que suporta l’estructura
quan el cotxe entra en el bucle, quan està situat verticalment i en el
punt més elevat del bucle.
Activitat
3: Calculeu la força extra que suporta l’estructura
quan el cotxe entra en el bucle, quan està situat verticalment i en el
punt més elevat del bucle.
![]() Activitat
4: Calculeu l’energia que té el cotxe
en cadascun dels instants anteriors.
Activitat
4: Calculeu l’energia que té el cotxe
en cadascun dels instants anteriors.
Anàlisi de les dades
![]() Activitat
5: Coincideixen els vostres càlculs teòrics
amb els que fa el Dr. Hugh Hunt en el vídeo de Fifth Gear TV?
Activitat
5: Coincideixen els vostres càlculs teòrics
amb els que fa el Dr. Hugh Hunt en el vídeo de Fifth Gear TV?
![]() Activitat
6: Entra el cotxe amb prou marge de seguretat?
Activitat
6: Entra el cotxe amb prou marge de seguretat?
![]() Activitat
7: Una vegada que el cotxe ha entrat en el bucle,
el conductor continua prement l’accelerador?
Activitat
7: Una vegada que el cotxe ha entrat en el bucle,
el conductor continua prement l’accelerador?
 |
| Fig 5: |
Solucions
A les qüestions a l’alumnat, que espero que siguin millorades pels estudiants que les responguin.
Activitat 1: Calculeu teòricament la celeritat mínima que hauria de portar el cotxe quan entra en el bucle i també en el punt més alt, per no caure.
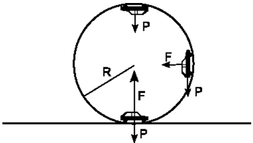
Si el cotxe passa pel punt més alt de la pista
,les forces que hi actuen en aquest moment són el propi pes i la força suplementària que hi fa la pista. La resultant de les dues l'obliguen a continuar girant circularment.
Aplicant la segona llei de Newton i tenint en compte que si en aquest moment la direcció de les forces (F i P) és vertical i cap avall, és a dir radial, l’acceleració que produiran és la normal, podem escriure:
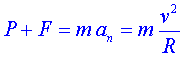 |
(1) |
I si aïllem la rapidesa que porta adalt,
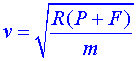 |
(2) |
Amb aquesta equació (2) podem calcular en general la celeritat que tindrà el cotxe en la part més alta de la trajectòria en funció de les forces que hi actuen.Però, quina és la rapidesa mínima? El radi de gir, la massa del cotxe i l’acceleració de la gravetat en aquell lloc són conegudes, l’única magnitud que pot canviar és la força (F) que fa la pista en elvehicle. Així doncs, com més petita és la força F menys celeritat porta el cotxe. On ésel límit? Quan la força que fa la pista sigui zero (perquè no pot ser negativa,ja que el cotxe no està enganxat al terra),llavors:
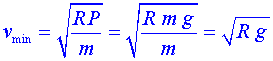 |
(3) |
És a dir, la celeritat mínima del cotxe en la part més alta només depèn del radi de la pista (i de la gravetat g a la Terra). Com en el nostre cas, R = 6 m.
| |
(4) |
Ara bé, per aconseguir passar per la part de dalt amb aquesta rapidesa mínima, amb quina celeritat ha d’entrar al bucle?Per trobar-la haurem de fer dues aproximacions en els càlculs que tenen efectes contraris,cosa que minimitza la incertesa en el resultat. Per una banda,el conjunt motor-rodes del cotxe no treballa quan està en el buclei, per una altra, el fregament de les peces del cotxe amb l’aire i l’estructura del bucle és menyspreable.
Si es donen aquestes dues condicions no hi haurà ni pèrdues ni guanys energètics i l’energia mecànica del sistema es conservarà:
|
(5) |
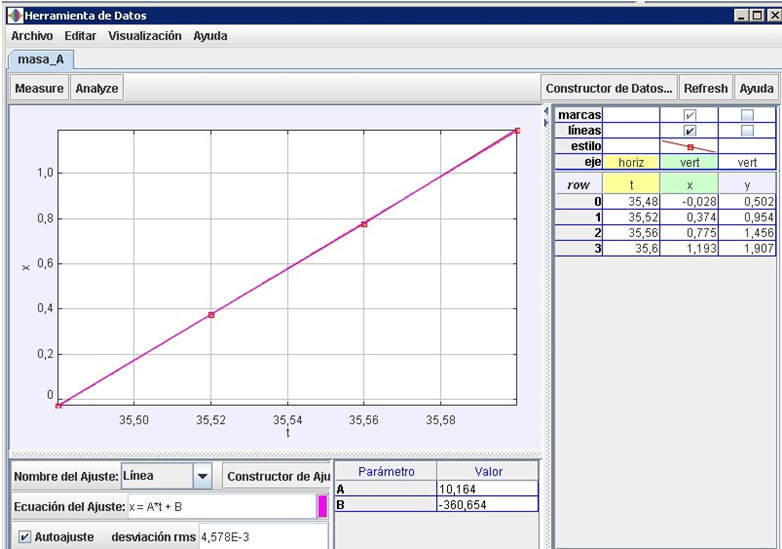
Activitat 2: Trobeu, amb l’ajut del Tracker, la rapidesa amb la qual el cotxe entra en el llaç, la que porta quan està vertical (un quart de volta) i la que té a dalt del tot del bucle..
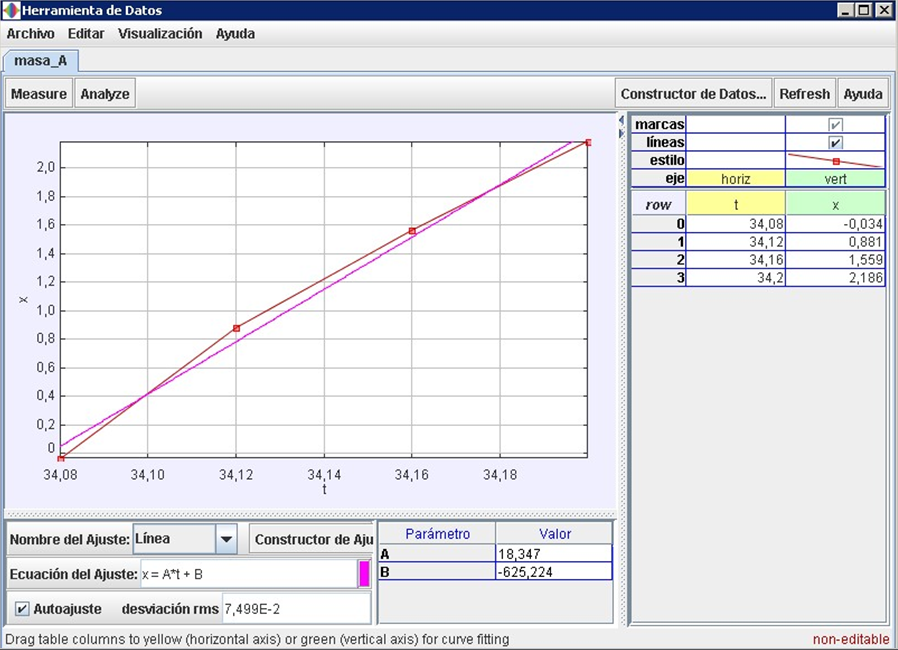
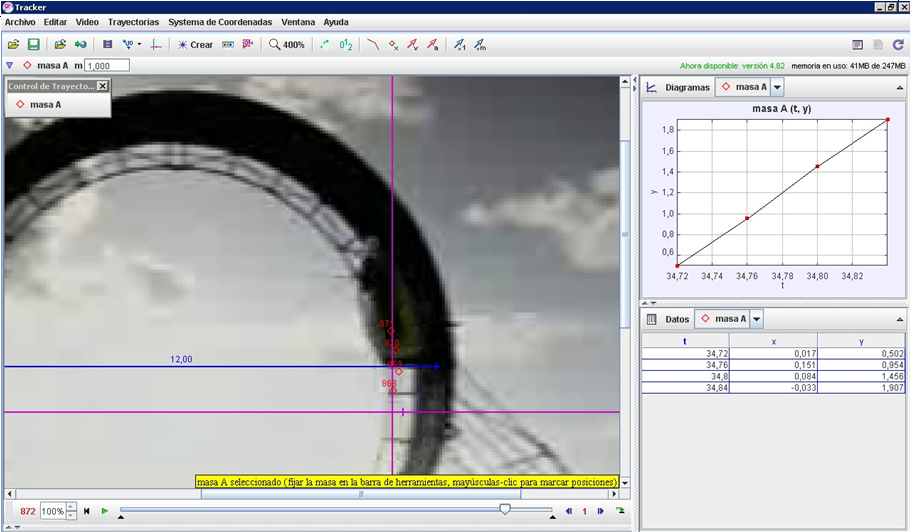
Obriuen el Tracker el vídeo de FifthGear i estudieu per separat cadascun dels trams, escollint un sistema de referència diferent per a cada situació (a baix, en vertical i a dalt de tot) en l’instant que considereu l’inici del moviment en cada cas. Per marcar els punts, us heu de fixar en algun element del cotxe que sigui prou distingible en cada tram. Per exemple, a baix he seguit el recorregut del retrovisor i a dalt el de la finestra. Així ens sortirà:En el moment en què entra en el bucle
:
(vegeu les figures 6 i 7).
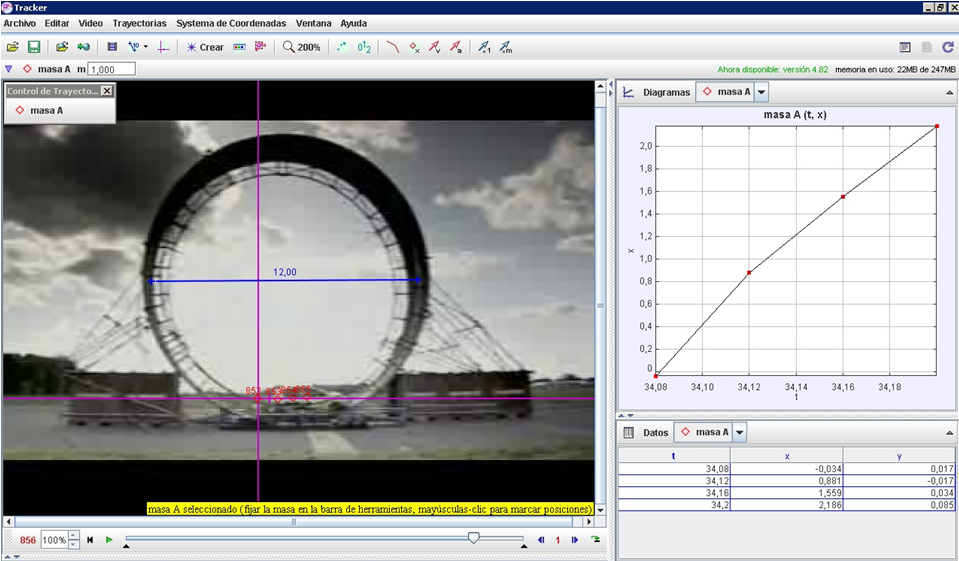 |
| Fig 6: |
Fig 7:
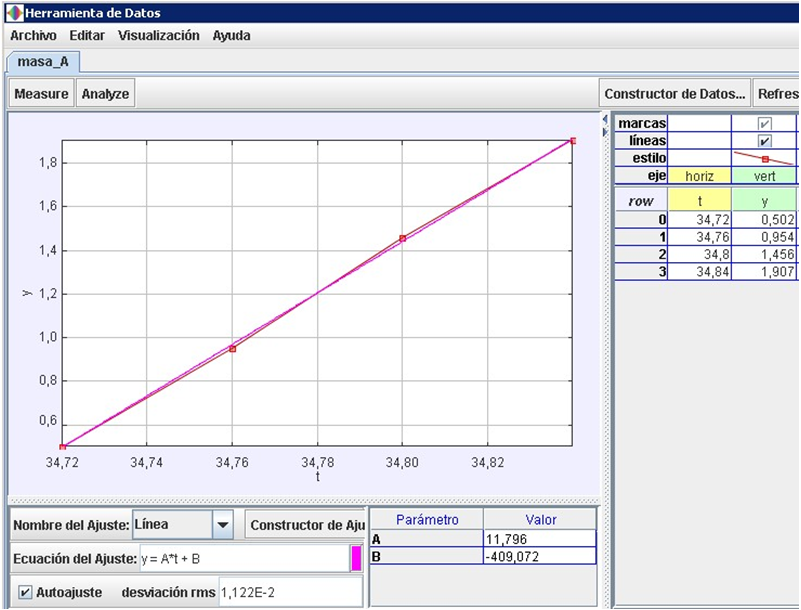
Quan està pujant verticalment
:
(vegeu les figures 8 i 9).
Fig 8:
Fig 9:
I en el punt més alt
:
(vegeu les figures 10 i 11).
Fig 10:
Fig 11:
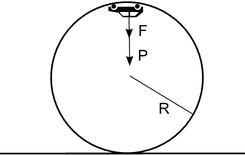
Activitat 3: Calculeu la força extra que suporta l’estructura quan el cotxe entra, quan està vertical i en el punt més elevat.
Fig 12:
Aquesta força extra (F) és la necessària per aguantar el pes (P) del vehicle i fer girar el cotxe en el bucle. En cada cas correspon a la força que juntament amb el seu pes proporciona al cotxe l’acceleració normal (
) que li permet girar. Veiem cada situació:
A l’inici del gir, en la part baixa,
, perquè l’estructura ha d’aguantar tot el pes del cotxe i alhora fer-lo girar.
En la situació vertical,
, per què el pes és perpendicular a l’acceleració normal.
I en el punt més alt,
, perquè només és el pes el que fa girar el cotxe quan la celeritat és la mínima.
Activitat 4: Calculeu l’energia que té el cotxe en cadascun dels instants anteriors.
L’energia mecànica del cotxe en cada moment serà la suma de l’energia cinètica i la potencial gravitatòria. Prenem com a posició de referència per al càlcul de l’energia potencial gravitatòria la base del bucle. Les celeritats són les obtingudes experimentalment amb el Tracker i per a la massa del cotxe prendrem la d’un Toyota Aygo com el del vídeo, que és de 790 kg.
Energia mecànica a l’inici:
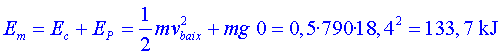
Energia mecànica en vertical:
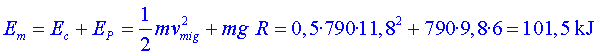
Energia mecànica a dalt de tot:
Activitat 5: Coincideixen els vostres càlculs teòrics amb els que fa el Dr. Hugh Hunt en el vídeo de Fifth Gear TV?.
Doncs sí. En tot cas faltaria per repetir un dels càlculs que fa el professor Hunt per conèixer l’acceleració a la qual estaria sotmès el pilot en fer el bucle.
Si volem calcular l’acceleració màxima hauríem de fer-ho quan el cotxe gira amb la celeritat màxima, que és en el moment en què inicia el gir. En aquest cas:
És a dir, aproximadament sis vegades l’acceleració de la gravetat, que és el que li surt al professor en el vídeo, una acceleració considerable però assumible per a un pilot de curses.
Activitat 6: Entra el cotxe amb prou marge de seguretat?
Teòricament el cotxe entra amb un cert marge de seguretat ja que la celeritat inicial mínima per no caure hem calculat que ha de ser de 17,2 m/s i la mesurada en la realitat ha estat de 18,4 m/s.
Ara bé, el risc d’accident és molt alt ja que si continués en el segon quadrant la mateixa pèrdua energètica que té en el primer, arribaria a dalt—si hi arribava—amb una energia mecànica de 69,3 kJ. Si intentem calcular la celeritat del cotxe en el moment crític tindríem:
És a dir, que la celeritat seria zero abans d’arribar a
i el cotxe cauria.
Tot això sense comptar el perill que l’estructura no aguanti els sobreesforços que es generen.
Activitat 7: Una vegada que el cotxe ha entrat en el bucle, el conductor continua prement l’accelerador?
Com s’aprecia en les respostes a les activitats 2 i 4, tant per la velocitat com per l’energia mecànica del cotxe en els tres punts estudiats, hi ha en el primer quadrant una disminució apreciable de la energia, de manera que podem suposar que el conductor aixeca el peu de l’accelerador. Posteriorment hi ha una recuperació de l’energia en el segon quadrant i això indica que el pilot torna a prémer l’accelerador.