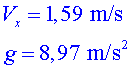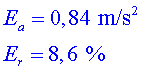Cada estiu, quan s’acaba el curs, tots, alumnes i professors, ens desitgem bones vacances i, qui més qui menys, ens dediquem a córrer món, alguns a prop de casa (a la costa catalana o les muntanyes del nostre país) i d’altres més lluny: alguna regió espanyola, ciutats o països europeus o, fins i tot, gràcies a l’avió, ens atrevim a travessar l’Atlàntic per anar a Amèrica o a gaudir del relax de països més exòtics.
L’alumnat, amb la seva família, tampoc no queda exclòs d’aquest període de descans i d’aquestes visites més o menys llunyanes.
És bo doncs aprofitar aquest fet per incorporar a la matèria de Física noves propostes d’exercicis i qüestions que sorgeixin de l’experiència personal, tant de l’alumnat com del professorat, durant el període estival. Així doncs, abans d’acomiadar-nos caldria posar-nos deures i no seria sobrer que, en recomençar el curs al setembre, cada alumne hagués d’aportar a l’aula algun detall, qüestió, fotografia, vídeo, anècdota... que ens serveixi per treballar algun aspecte de la Física i que a més estigui contextualitzat en la seva experiència personal. Potser una manera de fer deures agradable, curiosa i alhora engrescadora.
No cal dir que podem aprofitar aquesta proposta perquè l'alumnat presenti a la resta d'alumnes la seva proposta i sigui ell mateix qui els plantegi les qüestions relacionades amb la seva observació. D'aquesta manera aconseguim que els alumnes treballin i aprenguin de forma més competencial i amb entorns més contextualitzats, d'acord amb el que proposa el currículum. Fins i tot amb el recull d’exercicis, vídeos, fotografies... i les qüestions corresponents podem anar construint un bloc, de forma cooperativa, que els pot servir per estudiar, preparar els exàmens, preparar-se per a la selectivitat (la proposta seria molt semblant al bloc Houston... tenim uns problemes!, explicat recentment en un article d'aquesta revista).
Com a professors també podem utilitzar en els nostres exàmens aquestes aportacions de l'alumnat, cosa que donarà un punt més d'interès a l'alumnat en les qüestions plantejades i en la seva resolució.
A continuació us en presento alguns que us poden servir d’exemple i punt de partida per continuar la col•lecció... i en el proper número de la revista n'acabaré de presentar alguns més.
No cal dir que si disposeu d'exercicis, propostes, fotografies, vídeos... similars els podeu fer arribar a la redacció de la revista (redaccio@rrfisica.cat) i passaran a engruixir els articles sobre Física de viatges.
Senyal de trànsitUna foto de l'estiu del 2006 (vegeu la figura 1) d’un senyal de trànsit de límit de velocitat a Bèlgica... Hi veieu algun detall curiós o algun error? És clar que els responsables de la senyalització de trànsit belgues no tenien clar el tema de les unitats: al senyal correctehauria de posar 70 km/h o, en tot cas (com al nostre país), 70 a seques, ja que entenen s’entén que la velocitat es dóna en quilòmetres per hora ( km/h ) (que cal recordar que no és una unitat del sistema internacional d’unitats) però mai hi hauria de posar 70 km com a límit de velocitat permesa. Això és tan greu com posar en un cartell que la capital, Brussel·les, està a una distància de 50 kg. Proposta per a l'alumnat 
 |
| Fig. 1:Senyal de límit de velocitat a Bèlgica |
Si circuleu per les carreteres belgues (any 2006) us adonareu immediatament
d’un error molt greu. Observeu la fotografia i...
 Comenteu
quin és aquest error. Comenteu
quin és aquest error.
 Com creieu
que s’hauria de rectificar? Com creieu
que s’hauria de rectificar?
 És
absolutament certa la frase següent? A l’Estat espanyol aquest
error no existeix. És
absolutament certa la frase següent? A l’Estat espanyol aquest
error no existeix.
 Quina
modalitat de batxillerat creieu que va cursar el ministre d’Interior
belga? Quina
modalitat de batxillerat creieu que va cursar el ministre d’Interior
belga?
 Tenint
present que un senyal circular amb el contorn vermell i l’interior blanc
indica una prohibició, quina creieu que hauria de ser la interpretació
que els conductors haurien de fer del senyal de la fotografia? Tenint
present que un senyal circular amb el contorn vermell i l’interior blanc
indica una prohibició, quina creieu que hauria de ser la interpretació
que els conductors haurien de fer del senyal de la fotografia?

Pressió dins d’un avióSi hem volat en avió segur que, una vegada o una altra, hem patit mal d’orella a causa del canvi de pressió o, si més no, se’ns han destapat sobtadament en arribar a la destinació i fer un badall.
Sabem que els avions volen a una altura considerable (uns 10 km) i que a aquesta altura la pressió atmosfèrica és molt inferior a la que tenim al nivell del mar. De tota manera, un avió està pressuritzat per controlar la pressió que hi ha en tot moment dins de la cabina;en cas contrari, la variació sobtada del seu valor faria que la majoria de passatgers s’ho passessin bastant malament (manca d'oxigen, pressió baixa...).
Tot i que la cabina està pressuritzada, els pilots disminueixen la pressió interior entre altres factors per minimitzar la diferència de pressió entre l’interior i l’exterior i, d’aquesta manera, evitar esforços innecessaris al fuselatge de l’avió. Aquesta disminució de pressió es pot notar de diferents maneres. Per exemple, les bosses de xips (tancades hermèticament) que hem comprat a l’aeroport s’inflen de manera exagerada. Un altre cas: si mentre l’avió vola ens acabem l’aigua d’una ampolla (de PVC) i la tanquem hermèticament comprovarem que en aterrar l’ampolla s’ha aixafat apreciablement (figura 2). Podem utilitzar aquesta ampolla per calcular la pressió atmosfèrica que hi ha dins de l’avió en ple vol i comparar-la amb la pressió al nivell del mar i la que hi ha a l’altura normal de creuer dels avions.
Proposta per a l'alumnat 
 |
| Fig. 2:L'ampolla d'aigua quan l'avió ha aterrat. |
 Calculeu el volum de l’ampolla aixafada. Podeu fer-ho submergint-la
en un recipient gran i ple d’aigua i recollint l’aigua que en
vessa. Podeu mesurar el volum de l’aigua amb una proveta o pesant-la
i recordant que la densitat de l’aigua és .
Calculeu el volum de l’ampolla aixafada. Podeu fer-ho submergint-la
en un recipient gran i ple d’aigua i recollint l’aigua que en
vessa. Podeu mesurar el volum de l’aigua amb una proveta o pesant-la
i recordant que la densitat de l’aigua és .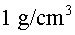
 Calculeu
després el volum de l’ampolla quan ha recuperat la forma inicial.
El volum d’aigua que conté ens pot ser útil en aquest
cas o bé podem repetir el procediment anterior per ser més precisos. Calculeu
després el volum de l’ampolla quan ha recuperat la forma inicial.
El volum d’aigua que conté ens pot ser útil en aquest
cas o bé podem repetir el procediment anterior per ser més precisos.
 Utilitzant la llei dels gasos a temperatura constant
Utilitzant la llei dels gasos a temperatura constant 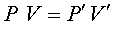 podeu calcular la pressió dins de l’avió.
podeu calcular la pressió dins de l’avió.
Utilitzeu la gràfica (figura 3) de la variació de la pressió
atmosfèrica amb l’altura.
 Compareu
aquesta pressió amb la que hi ha a l’exterior de l’avió
suposant que està volant a una altura d’uns 10000
metres. Compareu
aquesta pressió amb la que hi ha a l’exterior de l’avió
suposant que està volant a una altura d’uns 10000
metres.
 A quina
altura equival la pressió interior de l’avió? A quina
altura equival la pressió interior de l’avió?
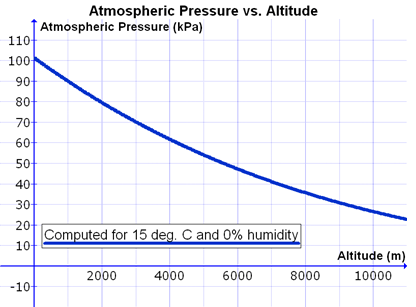 |
| Fig. 3: Gràfica de la variació de la pressió
atmosfèrica amb l'altura. |
 
L’aigua en caiguda lliureSabem, i ho hem repetit moltes vegades a l’aula, que el moviment de caiguda lliure correspon a una trajectòria parabòlica. A la part nova de l'outlet La Roca Village hi ha una font (figura 4) que projecta aigua (a vegades a intervals i a vegades de forma contínua) amb un angle i una velocitat determinats i que ens permet observar la trajectòria de l’aigua en caiguda lliure.
Podem capturar una fotografia d’aquesta font o bé fer-ne una gravació en vídeo. En la fotografia s'observa perfectament la trajectòria parabòlica i amb la gravació en vídeo podem analitzar el fenomen fotograma a fotograma amb un programa tipus MultiLab o Coach, per comprovar el valor de l’acceleració de la gravetat i també que el moviment de l’aigua és una composició d’un moviment rectilini uniforme horitzontal amb un moviment vertical amb acceleració constant (vertical i cap avall). Proposta per a l'alumnat 
 |
| Fig. 4: Font d'aigua a La Roca Village. |
Amb els programes MultiLab o Coach captureu les dades del moviment
del principi (o del final) d'un raig d'aigua al llarg de tota la seva trajectòria.
Nota: Aquí
us podeu baixar el vídeo corresponent a la font de la figura 4. Tingueu
en compte per fer el calibratge que la bossa de paper que es pot observar a
la part inferior dreta del vídeo té una alçada de 23
cm.
 Una vegada
capturades les dades, exporteu-les a un full de càlcul. Utilitzeu però
només les dades del vídeo corresponents al moviment de caiguda
lliure. Una vegada
capturades les dades, exporteu-les a un full de càlcul. Utilitzeu però
només les dades del vídeo corresponents al moviment de caiguda
lliure.
 Realitzeu
la gràfica x-t
del moviment i feu-ne un comentari qualitatiu. Realitzeu
la gràfica x-t
del moviment i feu-ne un comentari qualitatiu.
 Realitzeu
també la gràfica y-t
corresponent i comenteu-la. Realitzeu
també la gràfica y-t
corresponent i comenteu-la.
 A partir
de les gràfiques de tendència de les dues gràfiques (lineal
i polinomial de grau 2) obtingueu l'acceleració de la gravetat i la
velocitat (constant) horitzontal. A partir
de les gràfiques de tendència de les dues gràfiques (lineal
i polinomial de grau 2) obtingueu l'acceleració de la gravetat i la
velocitat (constant) horitzontal.
 Calculeu
l'error que es realitza amb aquest mètode per calcular la gravetat. Calculeu
l'error que es realitza amb aquest mètode per calcular la gravetat.
 Quines són les possibles fonts d'error? Proposeu algunes maneres de
solucionar-les.
Quines són les possibles fonts d'error? Proposeu algunes maneres de
solucionar-les.

Espectre de BrokenProposta per a l'alumnat 
 |
| Fig. 5: Espectre de Broken o ombra de l'avió envoltada d'una
glòria. |
Si viatgeu cap al tard amb avió (o a primera hora del
matí) i voleu per sobre d’un mar de núvols estigueu molt
atents a l’hora d’enlairar-vos o d’aterrar doncs és
possible que veieu un efecte òptic difícil d’observar: l’espectre
de Broken (vegeu la figura 5).
Aquest fenomen consisteix en que l’ombra d’un objecte o persona
(en aquest cas l’avió) es projecta sobre els núvols o la
boira i com a resultat tenim una imatge un pèl fantasmagòrica
(d’aquí el nom d’espectre).
Sovint el fenomen va acompanyat d’una difracció de la llum blanca
deguda als cristalls de gel o gotes d’aigua que formen el núvol.
Aleshores parlem de glòria i l’ombra projectada està envoltada
d’una circumferència de colors fent més atractiu el fenomen.

IridescènciesProposta per a l'alumnat 
 |
 |
| Fig. 6: Iridescències pujant al coll de la Marrana en els Pirineus
catalans |
Fig. 7: ...i a la Piràmide Vincent en la regió del
Monte Rosa |
Si aprofitem el període estival per fer alguna ascensió
a alguna muntanya relativament alta on la temperatura ambient és francament
baixa (Pirineus centrals, zones dels Alps...) podem tenir la sort d’observar
iridescències (figures 6 i 7) que es formen als núvols prims i
alts que estan formats per cristalls de gel que difracten la llum procedent
del sol.
Les iridescències ens apareixen com franges de colors semblants a l’Arc
de Sant Martí però les podem distingir perquè apareixen
al voltant del sol, recordem en canvi que l’Arc de Sant Martí l’observem
sempre d’esquenes al sol.
 Feu una
cerca a internet que us permeti explicar el fenomen de les iridescències. Feu una
cerca a internet que us permeti explicar el fenomen de les iridescències.

 
Solucions
Senyal de trànsit
 Comenteu quin és
aquest error. Comenteu quin és
aquest error.
Les unitats són incorrectes.
 Com creieu que s’hauria
de rectificar? Com creieu que s’hauria
de rectificar?
70 km/h
 És absolutament
certa la frase següent? A l’Estat espanyol aquest error no existeix. És absolutament
certa la frase següent? A l’Estat espanyol aquest error no existeix.
No és del tot correcta, faltarien les unitats.
 Quina modalitat de batxillerat
creieu que va cursar el ministre d’Interior belga? Quina modalitat de batxillerat
creieu que va cursar el ministre d’Interior belga?
Qualsevol batxillerat menys el científic.
 Tenint present que un
senyal circular amb un contorn vermell i l’interior blanc indica una
prohibició, quina creieu que hauria de ser la interpretació
que els conductors haurien de fer del senyal de la fotografia? Tenint present que un
senyal circular amb un contorn vermell i l’interior blanc indica una
prohibició, quina creieu que hauria de ser la interpretació
que els conductors haurien de fer del senyal de la fotografia?
D’aquí a 70
km no es pot circular per aquesta carretera o durant 70 km no es pot
circular.
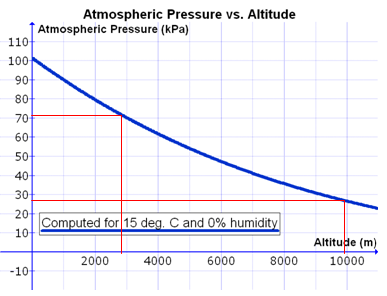 |
| Fig. 8: Gràfica de la variació de la pressió
atmosfèrica amb l'altura. |
Pressió dins d’un avió
 Calculeu el volum de l’ampolla
aixafada. Podeu fer-ho submergint-la en un recipient gran i ple d’aigua
i recollint l’aigua que en vessa. Podeu mesurar el volum de l’aigua
amb una proveta o pesant-la i recordant que la densitat de l’aigua és Calculeu el volum de l’ampolla
aixafada. Podeu fer-ho submergint-la en un recipient gran i ple d’aigua
i recollint l’aigua que en vessa. Podeu mesurar el volum de l’aigua
amb una proveta o pesant-la i recordant que la densitat de l’aigua és

En el nostre, cas hem mesurat un volum de 140
ml.
 Calculeu després
el volum de l’ampolla quan ha recuperat la seva forma inicial. El volum
d’aigua que conté ens pot ser útil en aquest cas o bé
podem repetir el procediment anterior per ser més precisos. Calculeu després
el volum de l’ampolla quan ha recuperat la seva forma inicial. El volum
d’aigua que conté ens pot ser útil en aquest cas o bé
podem repetir el procediment anterior per ser més precisos.
L'ampolla escollida era de 200
ml.
 Utilitzant la llei dels
gasos a temperatura constant Utilitzant la llei dels
gasos a temperatura constant 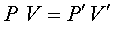 podeu
calcular la pressió dins de l’avió. podeu
calcular la pressió dins de l’avió.
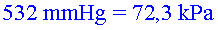
Utilitzeu la gràfica (imatge 3) de la variació de la pressió
atmosfèrica amb l’altura.
 Compareu aquesta pressió
amb la que hi ha a l’exterior de l’avió suposant que està
volant a una altura d’uns 10.000 metres. Compareu aquesta pressió
amb la que hi ha a l’exterior de l’avió suposant que està
volant a una altura d’uns 10.000 metres.
A aquesta altura, a l'exterior de l'avió només
hi ha uns 30 kPa
 A quina altura equival
la pressió interior de l’avió? A quina altura equival
la pressió interior de l’avió?
Equival a uns 3000
m d'altura.
L’aigua en caiguda lliure
Amb el programes MultiLab o Coach, captureu les dades del moviment del principi
(o del final) d'un raig d'aigua al llarg de tota la seva trajectòria.
Nota: Aquí
us podeu baixar el vídeo corresponent a la font de la figura 4. Tingueu
en compte per fer el calibratge que la bossa de paper que es pot observar a
la part inferior dreta del vídeo té una alçària
de 23 cm.
 Una vegada capturades
les dades, exporteu-les a un full de càlcul. Utilitzeu però
només les dades del vídeo corresponents al moviment de caiguda
lliure. Una vegada capturades
les dades, exporteu-les a un full de càlcul. Utilitzeu però
només les dades del vídeo corresponents al moviment de caiguda
lliure.
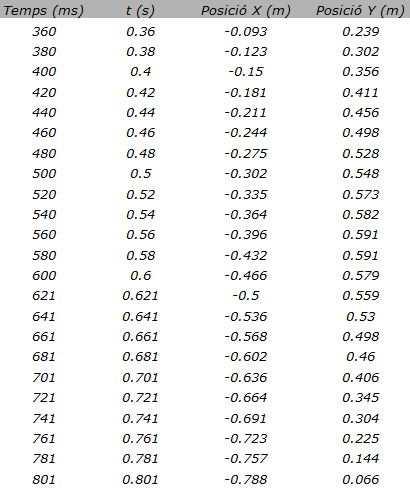 |
| Fig. 9: |
 Realitzeu la gràfica
x-t del
moviment i feu-ne un comentari qualitatiu. Realitzeu la gràfica
x-t del
moviment i feu-ne un comentari qualitatiu.
 Realitzeu també
la gràfica y-t
corresponent i comenteu-la. Realitzeu també
la gràfica y-t
corresponent i comenteu-la.
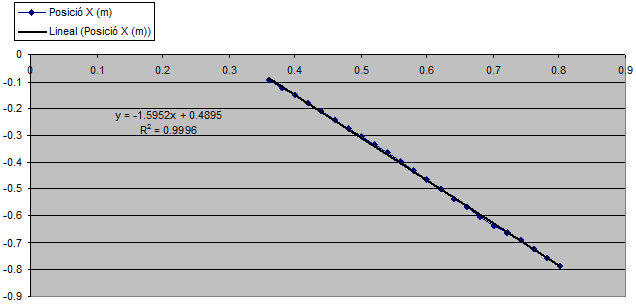 |
| Fig. 10: |
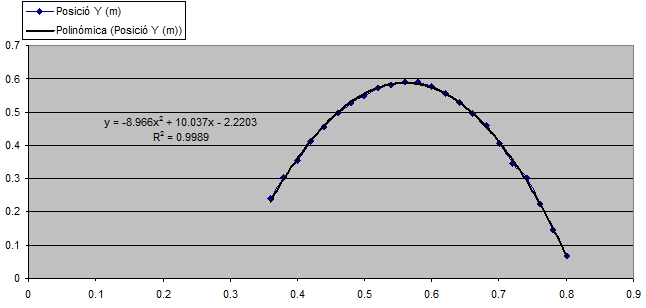 |
| Fig. 11: |
 A partir
de les gràfiques de tendència de les dues gràfiques (lineal
i polinomial de grau 2) obtingueu l'acceleració de la gravetat i la
velocitat (constant) horitzontal. A partir
de les gràfiques de tendència de les dues gràfiques (lineal
i polinomial de grau 2) obtingueu l'acceleració de la gravetat i la
velocitat (constant) horitzontal.
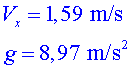
 Calculeu l'error que es
realitza amb aquest mètode per calcular la gravetat. Calculeu l'error que es
realitza amb aquest mètode per calcular la gravetat.
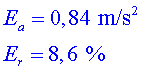
 Quines són les
possibles fonts d'error? Proposeu algunes maneres de solucionar-les. Quines són les
possibles fonts d'error? Proposeu algunes maneres de solucionar-les.
El moviment de la càmera provoca un canvi continu
de l'origen de coordenades. Hauríem de realitzar la filmació
amb un trípode.
El marcatge de cada punt és difícil. Hauríem d’utilitzar
una càmera que proporcionés imatges de més resolució.
La dispersió del raig d'aigua i el fregament corresponent amb l'aire.
En aquest cas, nosaltres no ho podem resoldre, el fenomen és així.
Iridescències
 Feu una cerca a Internet
que us permeti explicar el fenomen de les iridescències. Feu una cerca a Internet
que us permeti explicar el fenomen de les iridescències.
Una de les millors pàgines sobre fenòmens
òptics que conté moltes fotografies i explicacions molt detallades:
http://www.atoptics.co.uk

|

 2/8
2/8