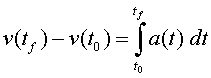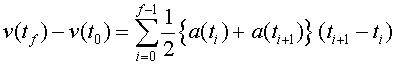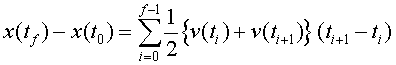Proposta
1. Introducció. L’exemple del cotxet de joguina lligat
a un contrapès
Una de les pràctiques més comunes que serveixen
per estudiar el moviment mitjançant sensors de posició és
el moviment d’un cotxet de joguina que es desplaça en línia recta
al llarg d’un carril. Al REVIR (el projecte de visites de centres de secundària
al laboratori digitalitzat de la UAB, on es treballa amb sensors i simulacions)
es fan diverses pràctiques experimentals que utilitzen un muntatge d’aquest
tipus, mitjançant el qual els estudiants d’ESO o de batxillerat estudien
el moviment rectilini uniforme (MRU) i el moviment rectilini uniformement accelerat
(MRUA).
En el cas d’aquestes pràctiques, el muntatge que s’utilitza
consta d’ un cotxet de joguina lligat a una corda, que alhora va lligada a un
contrapès que penja verticalment mitjançant una politja. L’experiència
consisteix a impulsar el cotxet amb una goma elàstica, de manera que
aquest surt disparat a gran velocitat. A causa de la tensió que la corda
fa sobre el cotxet, aquest va perdent velocitat a mesura que avança,
fins que s’atura. Tot seguit, com que la força tensió és
constant, el cotxet es comença a desplaçar en sentit contrari,
fins que torna al punt d’inici amb una velocitat en sentit invers al de la velocitat
inicial. Com que a l’extrem del carril hi ha un topall, quan el cotxet torna
a la posició inicial frena bruscament.
 |
| Fig. 1: Muntatge experimental del cotxet, lligat a la corda, que
es desplaça pel carril. |
Per descriure aquest moviment, podem parlar del “moviment d’anada” i del “moviment
de tornada”. El primer és el moviment que es produeix des que el cotxet
surt impulsat a gran velocitat fins que s’atura (en la figura 1, equivaldria
al moviment d’esquerra a dreta) i el segon és el moviment que fa el cotxet
des que està aturat fins que torna a la posició inicial (en la
figura 1, equivaldria al moviment de dreta a esquerra).
2. Anàlisi del moviment del cotxet a través
del sensor de posició
A través d’un sensor de distància situat a l’extrem
oposat del carril és fàcil mesurar la posició que el cotxet
té en cada moment i, per tant, obtenir una gràfica posició-temps
com la de la figura 2. En aquesta gràfica es pot observar com el cotxet
parteix d’una posició inicial allunyada del sensor, que comença
a desplaçar-se i dibuixa una paràbola (ja que, tan bon punt surt
disparat, el cotxet comença a frenar per l’efecte de la corda).
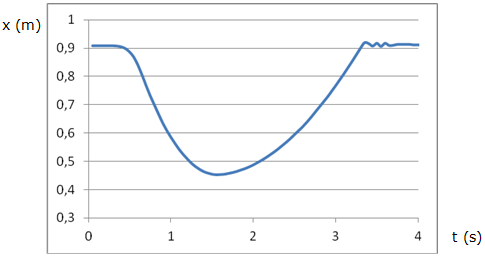 |
| Fig. 2:Gràfica posició-temps del cotxet obtinguda
amb el sensor de distància. |
A partir d’aquesta gràfica posició-temps, qualsevol programari
que utilitzi el sensor de posició per tractar les dades permet dibuixar
també gràfiques velocitat-temps i acceleració-temps. La
figura 3 permet veure que els moviments d’anada i de tornada són dos
MRUA amb acceleracions diferents. Això és degut a que les forces
que actuen no són exactament les mateixes: a l’anada el fregament s’afegeix
a la força de frenada de la corda, mentre que a la tornada aquestes dues
forces es contraresten, havent-hi així una força resultant (i
per tant, una acceleració) més petita.
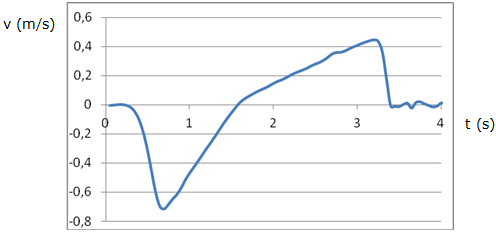 |
| Fig. 3:Gràfica velocitat-temps calculada a partir dels valors
mesurats amb el sensor de distància. |
Finalment, si representem la gràfica acceleració-temps (figura
4), podem identificar que també hi ha dos períodes amb acceleració
constant, que corresponen al moviment d’anada i de tornada del cotxet. No obstant
això, en aquesta gràfica són molt més vistosos els
“pics” d’acceleració que corresponen a l’instant concret en què
el cotxet surt disparat i el moment en què el cotxet s’atura bruscament
en tornar a la posició inicial.
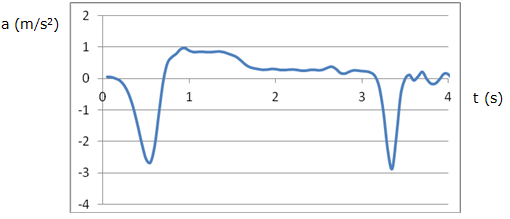 |
| Fig. 4:Gràfica acceleració-temps calculada a partir
dels valors mesurats amb el sensor de distància. |
3. Mesura de l’acceleració del cotxet a través
de l’acceleròmetre del mòbil
En comptes de mesurar la posició del cotxet amb un sensor
de distància, també podem utilitzar l’acceleròmetre (que
actualment porta incorporat qualsevol aparell mòbil) per
 |
| Fig. 5:Logotip de l’app “Accelerometer” |
mesurar l’acceleració del cotxet en funció del
temps. L’acceleròmetre dels mòbils funciona gràcies a una
minúscula peça metàl•lica subjectada mitjançant
uns també minúsculs serrells flexibles i elàstics que es
deformen amb el moviment de la peça mòbil. A través d’un
capacitador diferencial, la flexió d’aquests serrells produeix un senyal
elèctric que l’aparell processa per obtenir un valor d’acceleració
múltiple de g. De fet, l’acceleròmetre del mòbil permet
mesurar l’acceleració en els tres eixos del mòbil 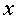 , ,
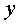 i i 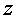 ,
tot i que nosaltres aquesta vegada només ens interessarà conèixer
l’acceleració en un únic eix: el de desplaçament del cotxet. ,
tot i que nosaltres aquesta vegada només ens interessarà conèixer
l’acceleració en un únic eix: el de desplaçament del cotxet.
Existeixen múltiples aplicacions disponibles que permeten mesurar l’acceleració
de l’aparell mòbil a temps real, totes amb funcionalitats molts semblants.
Una d’aquestes és l’aplicació “Accelerometer” (figura 5).
Tal com hem mostrat en la figura 1, hem incorporat un telèfon mòbil
a sobre del cotxet de joguina i l’hi hem subjectat per garantir que ambdós
cossos es moguin alhora. Un cop fet això, només hem de començar
a mesurar l’acceleració i reproduir el mateix moviment, impulsant el
cotxet i deixant que aquest faci el moviment d’anada i de tornada. L’aplicació
“Accelerometer” no només permet representar gràficament a temps
real el valor de l’acceleració, sinó també obtenir els
valors en format .txt, tot i que un cop obtingut un arxiu de text, les dades
es poden exportar a un full de càlcul. Per fer-ho, cal tenir en compte
que prèviament cal substituir els punts per les comes, ja que l’acceleròmetre
treballa amb notació anglosaxona (és a dir, utilitza el punt com
a separació decimal), mentre que els nostres fulls de càlcul estan
configurats per utilitzar la coma com a separació decimal. Un cop fet
aquest procés, ja podem representar gràficament l’acceleració
mesurada en funció del temps.
En la figura 6 representem els valors d'acceleració obtinguts amb l’acceleròmetre
(verd) i els acompanyem amb els valors d’acceleració que hem calculat
en la figura 4 a partir del sensor de distància (blau).
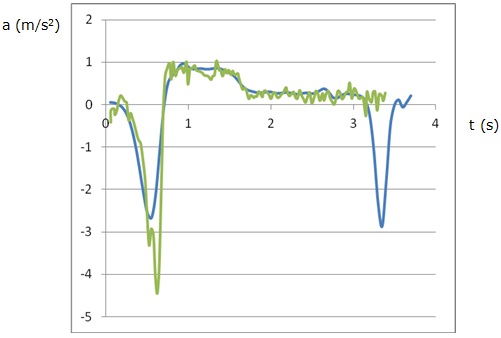 |
| Fig. 6:Gràfica acceleració-temps utilitzant tots
dos sistemes. |
Tot i que totes dues gràfiques són semblants, a simple vista podríem
pensar que la gràfica obtinguda amb l’acceleròmetre del mòbil
és molt més irregular i, per tant, més difícil de
llegir. No obstant això, cal tenir en compte que a l’escola poques vegades
es treballa amb gràfiques acceleració-temps, sinó que el
que ens interessa obtenir són les gràfiques de posició
i de velocitat. Per fer-ho, haurem de fer dos senzills càlculs.
4. Càlcul de la velocitat i la posició a partir
dels valors de l’acceleració.
Donada la relació diferencial 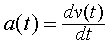 sabem
que per calcular la velocitat com a funció primitiva de l’acceleració
hem d’integrar la funció sabem
que per calcular la velocitat com a funció primitiva de l’acceleració
hem d’integrar la funció 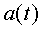
En el nostre cas, hem de fer una integració numèrica
amb el full de càlcul, que podem fer a partir de la relació.:
Al subíndex 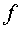 ,
que a l'expressió (1) vol dir "final", li
donem un valor númeric, ,
que a l'expressió (1) vol dir "final", li
donem un valor númeric,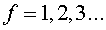 .
Així obtenim una col·lecció de valors .
Així obtenim una col·lecció de valors 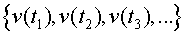 ,
que constitueixen la gràfica de la velocitat. Considerem que ,
que constitueixen la gràfica de la velocitat. Considerem que 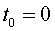 i anomenem
i anomenem 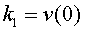 . Amb les
dades proporcionades per l'acceleròmetre ( figura 6 color verd) i considerant
que . Amb les
dades proporcionades per l'acceleròmetre ( figura 6 color verd) i considerant
que 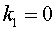 obtenim una gràfica
velocitat – temps com la de la figura 7, que veiem que s’assembla bastant a
la gràfica velocitat-temps que vèiem en la figura 3. obtenim una gràfica
velocitat – temps com la de la figura 7, que veiem que s’assembla bastant a
la gràfica velocitat-temps que vèiem en la figura 3.
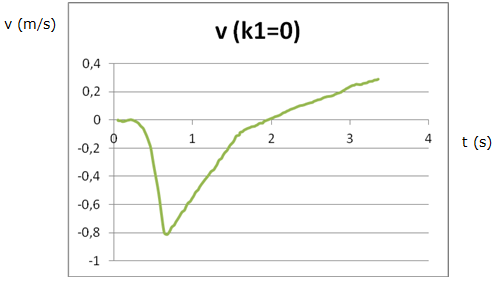 |
| Fig. 7:Gràfica velocitat-temps calculada a partir de la
integració numèrica. |
No obstant això, en tota integral existeix una constant d’integració
(en el nostre cas,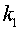 )
que cal definir a partir de les condicions específiques de la funció
primitiva. Per al moviment del cotxet, disposem d’una avantatge: sabem
que la velocitat zero coincideix en el moment exacte en què la funció
velocitat-temps canvia de pendent, ja que recordem que anteriorment
hem vist que les forces a l’anada i a la tornada no eren les mateixes i, per
tant, l’acceleració resultant dels dos moviments era també diferent. )
que cal definir a partir de les condicions específiques de la funció
primitiva. Per al moviment del cotxet, disposem d’una avantatge: sabem
que la velocitat zero coincideix en el moment exacte en què la funció
velocitat-temps canvia de pendent, ja que recordem que anteriorment
hem vist que les forces a l’anada i a la tornada no eren les mateixes i, per
tant, l’acceleració resultant dels dos moviments era també diferent.
Això ens permet ajustar la gràfica calculant el valor de 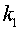 i aplicant en el full de càlcul la relació
i aplicant en el full de càlcul la relació 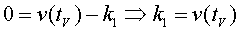 ,
on ,
on 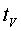 és el temps
en que es produeix el canvi de pendent. El valor de és el temps
en que es produeix el canvi de pendent. El valor de 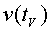 es pot veure directament a la gràfica de la figura 7. D'aquesta manera
obtenim una nova gràfica de la velocitat ajustada que poden veure a la
figura 8.
es pot veure directament a la gràfica de la figura 7. D'aquesta manera
obtenim una nova gràfica de la velocitat ajustada que poden veure a la
figura 8.
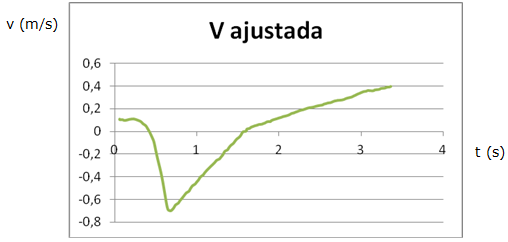 |
| Fig. 8:Gràfica velocitat-temps ajustada a partir de la gràfica
anterior. |
De la mateixa manera que hem fet amb la velocitat, també
podem calcular la posició del cotxet en funció del temps aplicant-hi
la relació
de manera que obtenim la gràfica de la posició
en funció del temps com la de la figura 9. En aquest cas, de nou, trobem
que la posició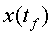 depèn de l’origen de coordenades seleccionat. Per tant, hauríem
de tornar a ajustar la gràfica mitjançant una segona constant
d’integració
depèn de l’origen de coordenades seleccionat. Per tant, hauríem
de tornar a ajustar la gràfica mitjançant una segona constant
d’integració 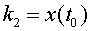 .
.
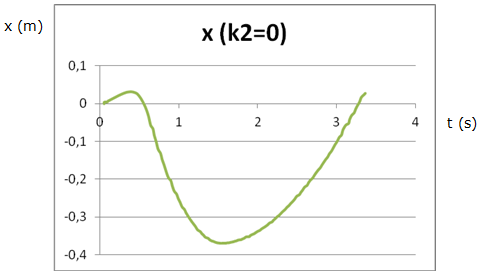 |
| Fig. 9:Gràfica posició-temps calculada a partir de
la integració numèrica. |
5. Comparació entre els dos sistemes de captació
de dades: avantatges i inconvenients de cadascun
Podem comparar la gràfica posició-temps de la
figura 2 amb la de la figura 9 i trobem que totes dues tenen un aspecte molt
semblant. En el primer cas, les dades enregistrades corresponen a la posició
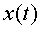 del cotxet, a partir
de la qual s’han calculat del cotxet, a partir
de la qual s’han calculat 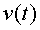 i
i 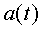 . En el segon cas,
les dades enregistrades corresponen a l’acceleració . En el segon cas,
les dades enregistrades corresponen a l’acceleració 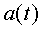 ,
a partir de la qual s’ha calculat v(t) i ,
a partir de la qual s’ha calculat v(t) i 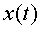 .
Quins avantatges i inconvenients té cada sistema de captació de
dades? .
Quins avantatges i inconvenients té cada sistema de captació de
dades?
El principal avantatge del sensor de distància és que permet als
estudiants visualitzar la gràfica 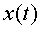 a temps real. Això els permet veure com s’està desplaçant
el cotxet i alhora com es va dibuixant la gràfica que en descriu la posició.
En canvi, utilitzant l’acceleròmetre del mòbil, la gràfica
que s’obté a temps real és una gràfica
a temps real. Això els permet veure com s’està desplaçant
el cotxet i alhora com es va dibuixant la gràfica que en descriu la posició.
En canvi, utilitzant l’acceleròmetre del mòbil, la gràfica
que s’obté a temps real és una gràfica 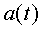 ,
molt més difícil de llegir, ja que és molt menys intuïtiva.
Si es vol obtenir la gràfica ,
molt més difícil de llegir, ja que és molt menys intuïtiva.
Si es vol obtenir la gràfica 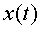 , que, de fet, és la gràfica que els estudiants poden interpretar
més fàcilment , cal que aquests exportin el document .txt que
genera l’app i que obrin un full de càlcul, cosa que fa que es perdi
la immediatesa que ofereix el sensor de distància.
, que, de fet, és la gràfica que els estudiants poden interpretar
més fàcilment , cal que aquests exportin el document .txt que
genera l’app i que obrin un full de càlcul, cosa que fa que es perdi
la immediatesa que ofereix el sensor de distància.
Ara bé, el principal avantatge de l’acceleròmetre és que
és molt més accessible que el sensor de distància. Aquests
dispositius solen ser cars i tot i la dotació que el Departament d'Ensenyament
va fer als centres de secundària durant la dècada passada, actualment
en molts instituts aquests sensors estan malmesos i utilitzen un programari
desfasat. La inversió econòmica que els centres poden fer per
adquirir nous sensors es limita a 1 o 2 sensors per institut, cosa que no permet
la recollida de dades experimentals en petits grups d’estudiants. En canvi,
en la majoria de centres és fàcil trobar un grup d’adolescents
en què, com a mínim, un d’ells disposi d’un telèfon mòbil
amb l'acceleròmetre incorporat. Un altre avantatge d’utilitzar l’acceleròmetre
del mòbil és que, més enllà de la mesura d’aquesta
pràctica concreta, permet endinsar-se en la funcionalitat de l’acceleròmetre
i en els altres sensors dels dispositius electrònics actuals.
Per acabar, també és interessant poder combinar tots dos sistemes
de captació de dades i poder compartir amb els estudiants les reflexions
que aquí s’exposen sobre la naturalesa de cada tipus de dades.
6. Dades obtingudes
En el full de càlcul adjunt (full_calcul.xls
, full_calcul.ods)
trobem un conjunt de dades enregistrades amb el sensor de distància i,
posteriorment, amb l'acceleròmetre del mòbil. L'experiment, tal
com he explicat en el text, es repeteix amb les mateixes condicions de manera
que els resultats han de ser pràcticament idèntics.
En les diferents columnes del full de càlcul podem observar les fórmules
utilitzades per realitzar els càlculs de la velocitat i l'acceleració
a partir dels valors de la posició i també del procés d'integració
per obtenir la velocitat i la posició a partir de les dades provinents
de l'acceleròmetre.
Bibliografia

|

 5/8
5/8