Introducció

Fig. 1

El sensor Tag és un aparell de dimensions semblants a un comandament a distància i amb un preu aproximat de20€.

A la figura 1 podem veure el sensor Tag de color vermell, al costat d’unes claus de cotxe.
Aquest sensor incorpora una colla de sensors electrònics que permeten mesurar:

• La temperatura ambient.
  
• La temperatura superficial (IR)
  
• La pressió atmosfèrica.
  
• La humitat.
  
• L’acceleració (conté un acceleròmetre 3D).
  
• L’angle girat (conté un giroscopi 3D).
  
• El camp magnètic (conté un magnetòmetre de tres eixos).

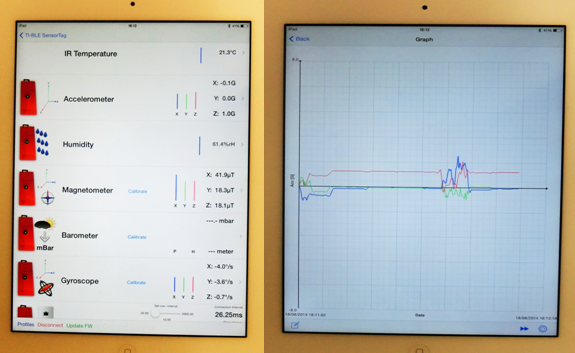
Aquest sensor envia les dades via ràdio a un telèfon mòbil intel•ligent o a una tauleta, d’on es poden visualitzar. A partir d’aquests dispositius es poden enviar les dades per correu electrònic en forma de fitxer Excel a qualsevol usuari.
Les dades que proporciona aquest aparell són uns gràfics de cada magnitud en funció del temps (l’escala de temps entre mesures es pot escollir dins d’uns marges per a cada sensor) que es poden visualitzar en forma de diagrama en la tauleta o al mòbil. Després, podem treballar aquests gràfics a l’ordinador per fer l’estudi que ens interessi.
La proposta didàctica que es pot fer amb aquest dispositiu per engrescar una mica els alumnes treballant amb el mòbil i amb tecnologies d’última generació, és realitzar una experiència i després capturar-ne els resultats individualment o en petits grups per treballar-hi. També es poden comprar uns quants sensors per treballar diferents experiències i posar-ne en comú o comparar-ne els resultats. Si no disposem de mòbils o no els volem fer servir, també venen un port USB que es pot acoblar al portàtil o a l’ordinador i fa les mateixes funcions.

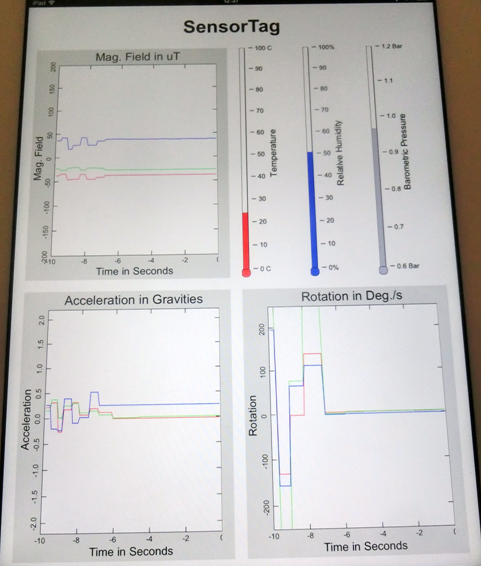
A l’hora de capturar els resultats tenim dues opcions (apps) que podem descarregar de les adreces que es donen al manual del sensor. N’hi ha una per al sistema Apple i una per a l’Android,(em sembla que funciona millor la de l’Apple a l’hora de veure els diagrames) . En l’una es veuen simultàniament totes les mesures i l’aparença que té és la de la imatge que tenim a sota.(fig2)

Fig. 2

I, a l’altra, que és una mica més completa i s'hi veuen tots els paràmetres. Per visualitzar un gràfic hem de situar el cursor en la mesura concreta i es escollir l’opció de veure que gràfic. Podrem triar dues opcions: "amb àrees" o "amb línies". La forma que adopta la podem veure a les imatges següents:

Fig. 3

Les pantalles que obtenim en aquesta aplicació serien primer la de l’esquerra i, després, quan volguéssim mesurar un paràmetre concret, la de la dreta. També podem escollir, mitjançant una opció que tenim en la part inferior esquerra de la primera pantalla i que s’anomena “Profiles”, el temps que triga el sensor a repetir la mesura. Normalment podem escollir entre 0,1 i 2,5 segons. A la imatge inferior podem veure a questa pantalla.

Fig. 4

Exemple d'aplicació

Estudi del moviment circular en la perifèria d'una llanda de bicicleta

Per veure les possibilitats que té aquest sensor, l’hem enganxat a una llanda de bicicleta tal com es mostra en la figura 5. La roda gira en el pla vertical perpendicular al nord.

Fig. 5

Hem posat un eix a la llanda i l’hem fet rodar donant-hi un impuls primer en el pla horitzontal i després en el pla vertical amb direcció perpendicular al nord.
El moviment té dues etapes. En la primera nosaltres accelerem la roda amb una força que depèn del temps (en els gràfics podem comprovar que és gairebé lineal); en la segona etapa, la roda es va frenant a causa del fregament i l’acceleració esmanté gairebé constant o bé varia lleugerament en el temps amb un pendent molt petit.

Pla horitzontal

Hem posat l’eix perpendicular al pla horitzontal, hi hem donat un impuls i hem capturat dos gràfics de forma simultània.

A- L’acceleròmetre (tres eixos ,i ), no permet calibrar. Hem escollit fer les mesures cada 0,1s.

B- El magnetòmetre permet calibrar el punt inicial, que és el zero, i mesurar les variacions que detecta respecte a aquest punt. Hem escollit fer les mesures cada 0,1 s.

Les coordenades ,i amb què mesurem el camp magnètic terrestre, es defineixen de la manera següent::
La coordenada assenyala al pol nord geogràfic. La coordenada assenyala cap a l’est, i la coordenada és la perpendicular al terra amb el sentit positiu cap al seu centre, perquè aquesta és la direcció i el sentit del camp magnètic terrestre al pol nord. Si és el vector camp magnètic, és el mòdul d’aquest vector, és a dir l’arrel quadrada de la suma dels quadrats de les tres components, en les direccions ,i .

Els gràfics que hem obtingut són els següents:

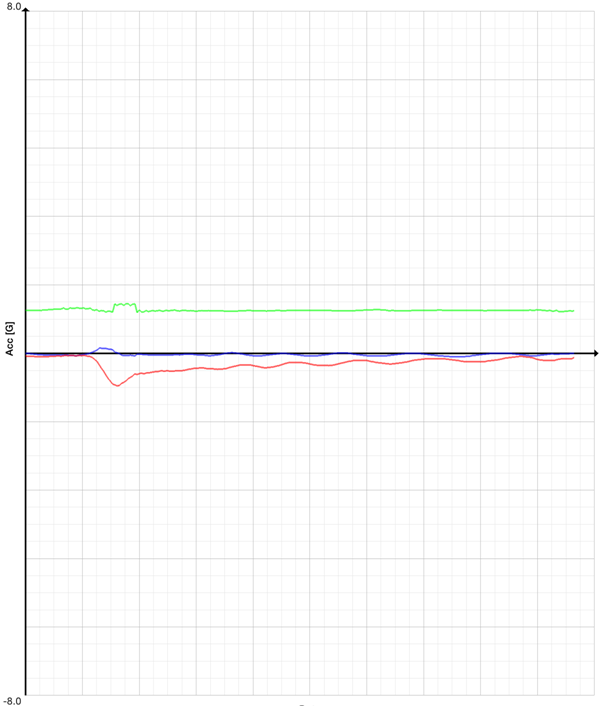
Gràfic 1: acceleròmetre

En el primer gràfic tenim l’acceleració (eix ), que es mesura en G (G=9,8 m/s²) cada divisió correspon a 0,4G, i el temps (eix ) que es mesura en segons . Cada divisió correspon a 0,1 s.
Podem observar en el moment de donar impuls a la roda que hi ha una variació brusca en la component de color vermell, quan deixem d’impulsar la roda, el pendent de la component de color vermell canvia de signe.

Fig. 6

A partior del gràfic podem calcular la força d’impulsió que depèn del temps de forma lineal. Cada divisió vertical correspon a 0,4 G (G=9,8 m/s²) i cada divisió horitzontal a 0,1 s. De la manera que hem posat el sensor, veiem que els signes dels pendents van al revés . La força impulsiva actua entre 0,45 s i 0,65 s i suposa un increment en l’acceleració de 0,8G. Per tant, l’acceleració en aquest interval de temps serà :.

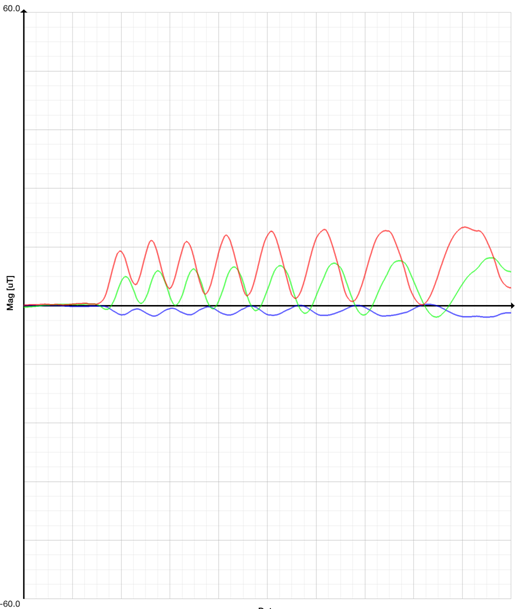
Gràfic 2: magnetòmetre

Cada divisió vertical correspon a i cada divisió horitzontal a 0,1 s.
Com que el magnetòmetre es pot calibrar, comencem el moviment en zero. El sensor farà les mesures respecte a la posició inicial. El nombre de voltes coincideix amb el nombre de màxims que podem observar en el gràfic, en aquest cas 8 voltes. Les components i del camp magnètic corresponen als colors vermell i verd, i la component (vertical) correspon al color blau que experimenta una variació molt petita. Mesurant la distància entre els màxims podríem calcular l’acceleració de frenada però d’una forma més imprecisa que amb el gràfic que proporciona l’acceleròmetre.

Fig. 7

Pla vertical

Hem posat l’eix paral•lel al pla horitzontal i perpendicular al nord, hi hem donat un impuls i hem capturat dos gràfics de forma simultània.

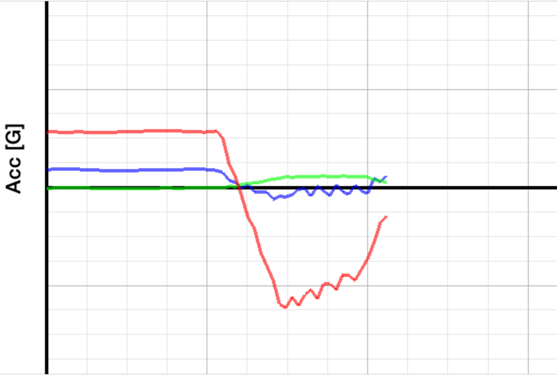
Gràfic 3: acceleròmetre

En el tercer gràfic tenim l’acceleració (eix ), que es mesura en G(G=9,8 m/s²), i el temps (eix ), que es mesura en segons. Cada divisió correspon a 0,1 s.
Podem observar qu een el moment de donar impuls a la roda hi ha una variació brusca en la component de color vermell: quan deixem d’impulsar la roda, el pendent de la component de color vermell canvia de signe.

Fig.8

Igual que en el cas anterior, podem calcular l’acceleració motriu, que veiem que depèn del temps de forma lineal. En aquest cas, l’interval de temps va de 0,42 s a 0,57 s, l’acceleració varia 7 divisions, . Per tant
En aquest gràfic podem observar que la component vermella té 5 mínims (que haurien de ser màxims) i corresponen al nombre de voltes que ha donat la roda.

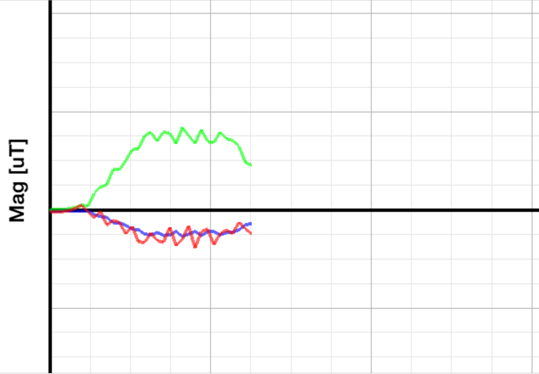
Gràfic 4: magnetòmetre

Cada divisió vertical correspon a i cada divisió horitzontal a 0,1 s.
En aquest gràfic, igual que en el cas anterior, podem comptar el nombre de voltes que corresponen als màxims que en són 5 . Coincideix amb l’acceleròmetre. En aquest exemple, l’acceleració és molt gran i com que fem les mesures cada 0,1s no podem observar les corbes tan ben diferenciades com en l’exemple anterior (pla horitzontal).

Fig. 9

Conclusions de l'experiment

L’acceleròmetre de tres eixos ens és útil per calcular l’acceleració. En el cas presentat podem veure un exemple pràctic d’acceleració motriu que varia de forma lineal amb el temps i que es pot calcular fàcilment amb els alumnes. El magnetòmetre mesura només les variacions del camp magnètic terrestre. És un instrument molt útil per mesurar el nombre de voltes, tant en el pla horitzontal com en el vertical.

El PocketLab

Fig. 10

Als Estat Units fan servir un aparell semblant al sensor Tag però molt més robust (a prova de nens), amb una mica més d’abast (la senyal es pot captar de més lluny; també funciona molt bé amb el sistema Android ), encara que amb un preu superior (al voltant dels 100$). Els sensors que incorpora són les mateixos que el sensor Tag i les mesures també, però amb una mica més de fiabilitat i amb la possibilitat de compartir-les i exposar-les, tal com s'explica a la pàgina web : http://thepocketlab.com/

On podem comprar el sensor Tag?

Podem comprar el sensor Tag per Internet a les adreçes següents :

• http://www.ti.com/tool/cc2541dk-sensor
  
• http://es.farnell.com/texas-instruments/cc2541dk-sensor/cc2541-sensortag-bluetooth-dev/dp/2334329?ost=sensor+tag
  
• http://www.digikey.es/product-search/en/programmers-development-systems/evaluation-boards-sensors/2622557?k=cc2541

Bibliografia

• Fundamentos de geofísica. Agustín Udías, Julio Mezcua. 1997 Alianza Editorial.
  

ISSN: 1988-7930 DL:  B-31773-2012   Adreça a la xarxa: www.RRFisica.cat    Adreça electrònica: redaccio@rrfisica.cat  difusio@rrfisica.cat
Comitè de redacció : Josep Ametlla, Octavi Casellas, Xavier Jaén, Gemma Montanyà, Octavi Plana, Jaume Pont.
Treballem conjuntament : Societat Catalana de Física, Associació de Professores i Professors de Física i Química de Catalunya,XTEC, Universitat Politècnica de Catalunya, Universitat de Barcelona

Recursos de Física col·labora amb la baldufa i també amb ciències Revista del Professorat de Ciències de Primària i Secundària (Edita: CRECIM-UAB)