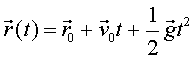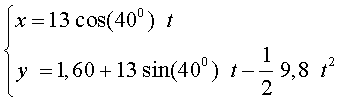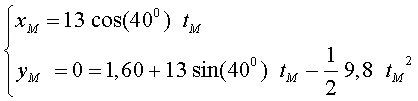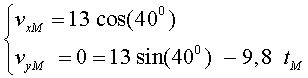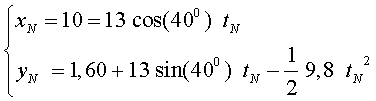núm 2 |
Tardor del 2008 |
Societat Catalana de Física |
| Inici |
| Sumari |   9/9 9/9 |
| Problemes d'aquí i d'allà Salvador Estradé |
|
| L’objectiu d’aquesta secció és proposar i resoldre problemes que siguin estimulants i atractius per a l’alumnat (i per a nosaltres) i que en fomentin l'interès per la física. Voldríem que el professorat s’animés a col·laborar-hi, que ens enviés les seves propostes a sestrade@xtec.cat i que engresqués el seu alumnat a participar-hi. En cada número, hi haurà una proposta i se'n publicarà la millor solució o la més original. |
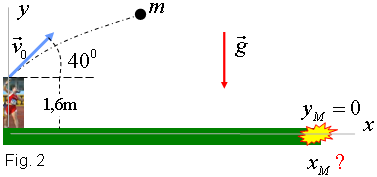
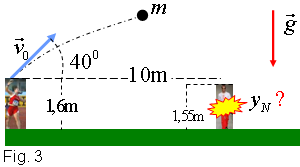
La llançadora de pesEn aquest número, us proposem un problema que sintonitza amb l'estiu olímpic que hem viscut tots plegats. Enunciat
La llei de moviment de Newton
Prenent com a origen de coordenades el punt del terra de l'estadi
corresponent a la vertical del llançament, tenim que
a) Per conèixer la marca de llançament de l'atleta cal calcular l'abast d'aquest moviment parabòlic. Si anomenen M el punt d'impacte de la bola amb el terra, sabem que aquest punt ha de complir:
Si es resol la darrera equació s'obté tM = 1,88 si, si s’hi substitueix la primera, trobem que l'abast màxim és de xM =18,7 m b) Els components de la velocitat de la bola en el moment de l'impacte valen:
i el mòdul, Substituint i operant, obtenim que vM = 14,2 m/s.
c) Per saber si hi haurà o no un accident, cal trobar a quina altura està la bola quan ha recorregut horitzontalment 10 m i comparar-la amb l'altura del jutge. Si anomenem N aquest punt de la trajectòria de la bola, tenim:
Resolent la primera equació, obtenim que tN = 1 s, i, substituint la segona, dóna que l'altura a la qual passa la bola pel lloc on és el jutge és de yN =5,06 m. Així doncs, no impactarà en el jutge. d) D'una banda, és
obvi que l'abast del moviment parabòlic i la possibilitat d'un accident
depenen de l'angle de llançament. Només cal llançar la
bola en un angle recte i esperar uns instants! D'altra banda, si haguéssim
resolt el segon apartat per conservació de l'energia mecànica
de la bola entre el punt de llançament i el d'arribada a terra, hauríem
vist que el mòdul de la velocitat d'arribada (no els components) és
independent de l'angle de llançament i que únicament depèn
de l'altura del punt de llançament (que en aquest cas suposem que no
ha canviat del primer al segon intent). Per tant, l'única magnitud que
podem assegurar que no canviarà en els dos llançaments és
el mòdul de la velocitat d'impacte amb el terra. 
|
|||||||||||||||||