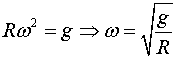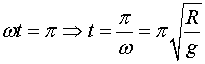La solució del problema del número anterior la trobareu, junt amb l'enunciat, seguint l'enllaç: Hurakan Condor Les virolles d'en SchumacherEn
aquest número us presentem un problema basat en el dubte que
genera una seqüència d'un vídeo d'una coneguda marca
de cotxes en què es veu com un cotxe fa una virolla enfilant-se
per la paret d'un túnel. Segons les dades que es poden extreure
del vídeo, ens queda el dubte de si és un muntatge o la
virolla és real. Què diuen els vostres estudiants?  
Enunciat
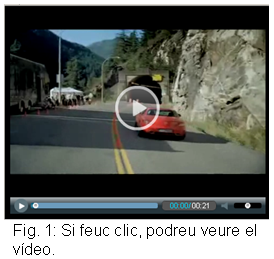
| En un anunci d'una coneguda marca de cotxes (que podeu
reproduir fent clic a la figura 1) es veu a Michael Schumacher fent una
virolla a l'interior d'un túnel. La seqüència de la
virolla la reproduïm amb tres fotogrames a la figura 2. Segons ens
mostra el vídeo, si no hi ha alguna mena de muntatge, triga uns
4 segons a
fer la virolla.

|
|
Fent un càlcul visual (figura 3), observem que,
si el cotxe té uns 2
metres d'amplada, el túnel tindrà, com a mínim, uns
10 metres d'amplada.
Ens podem creure, segons la física i amb les dades que tenim, que
Michael fa realment aquesta virolla?
|

|
Solució
Solucionem el problema observant el cotxe des d'un
sistema de referència inercial que es mou amb velocitat constant
en la direcció del túnel i mòdul igual a la velocitat
del cotxe en aquesta direcció, 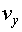 .
Des d'aquest sistema veiem que el cotxe realitza un moviment circular
uniforme amb velocitat .
Des d'aquest sistema veiem que el cotxe realitza un moviment circular
uniforme amb velocitat 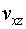 ( vegeu la figura 4).
( vegeu la figura 4).
La velocitat mínima del cotxe per fer la virolla ha de ser tal
que la seva component transversal al túnel,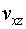 , faci que la reacció normal sigui, com a molt petita, igual a
zero. D'aquesta manera es garanteix que el cotxe no perd el contacte amb
el terra de la pared del túnel, és a dir, que no cau.
, faci que la reacció normal sigui, com a molt petita, igual a
zero. D'aquesta manera es garanteix que el cotxe no perd el contacte amb
el terra de la pared del túnel, és a dir, que no cau.
Així, si el túnel fa R=5m
de radi:
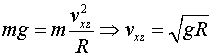
Si tenim en compte que per fer la virolla el cotxe ha de recórrer
una longitud transversal 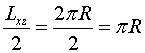 ,
el temps invertit serà: ,
el temps invertit serà:
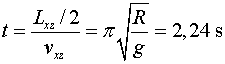
|
 |
Que és un temps bastant més petit que l'utilitzat per en Shumacher
a l'anunci. Així, tot sembla indicar que l'anunci no és del tot
realista!
Guia del professorat 
La justificació de la manera de procedir anterior
és dir que plantegem les lleis de la mecànica en un sistema
de referènca inercial que viatja amb velocitat constant 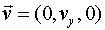 respecte
del sistema de referènca fix al túnel. Així , respecte
d'aquest sistema de referència mòbil, la trajectòria
del cotxe és un moviment circular de velocitat constant amb mòdul
igual a respecte
del sistema de referènca fix al túnel. Així , respecte
d'aquest sistema de referència mòbil, la trajectòria
del cotxe és un moviment circular de velocitat constant amb mòdul
igual a 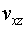 . .
Si el problema el volem solucionar en el sistema de
referència fix al túnel tenim que, de fet, el cotxe fa
una trajectòria en forma d'hèlix de radi R
i pas de rosca constant H.
La velocitat del cotxe per aquesta trajectoria és v.
Utilitzarem el radi de curvatura de l'hèlix  i el fet que el cotxe, al fer la virolla, recorre una longitud
i el fet que el cotxe, al fer la virolla, recorre una longitud 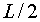 .
Donem sense demostració les expresions d'aquestes magnituds: .
Donem sense demostració les expresions d'aquestes magnituds:
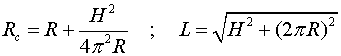
Utiitzant ara les mateixes expressions d'abans, aplicades
ara a la trajectòria en hèlix, trobem
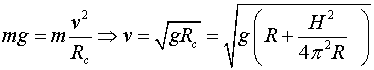
la velocitat que es requereix depèn, com era d'esperar,
del pas de rosca, és a dir de la llargada de la virolla. |
 |
Ara el temps:
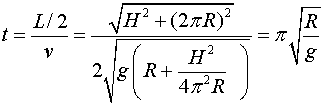
Que resulta ser independent de la llargada de la virolla i
coincideix amb el càlcul que hem fet en el sistema de referència
inercial mòbil, com era d'esperar!
Evidenment tot això sembla força complicat. Una
altra manera de fer les coses és resoldre el problema a partir de l'expressió
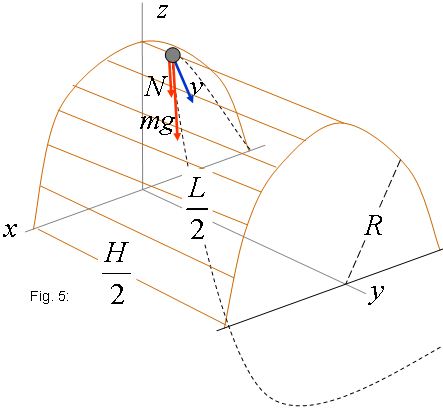
de la trajectòria i la llei moviment de Newton. La trajectòria,
amb les condicions inicials a l'inici de la virolla ( vegeu la figura 5), és
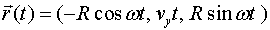 . L'acceleració
la trobem derivant dos cops . L'acceleració
la trobem derivant dos cops 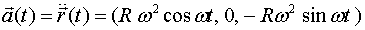
Ara apliquem 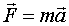 al punt més alt de la trajectòria. En aquest punt el temps compleix
al punt més alt de la trajectòria. En aquest punt el temps compleix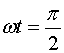 .
Prenent la normal nul·la tindrem .
Prenent la normal nul·la tindrem
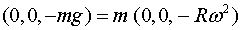
D'aquí obtenim
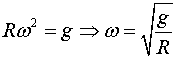
Així, el temps que triga en fer tota la virolla serà
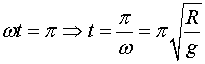
que coincideix amb el temps obtingut anteriorment.
| Inici |
|
|
| ISSN:
1988-7930 Adreça a la xarxa:
www.RRFisica.cat Adreça electrònica:
redaccio@rrfisica.cat
difusio@rrfisica.cat
Comitè de redacció : Josep Ametlla, Octavi
Casellas, Xavier Jaén, Gemma Montanyà, Cristina Periago,
Octavi Plana, Jaume Pont i Ramon Sala.
Treballem conjuntament : Societat Catalana de Física,
Associació de Professores i Professors de Física i Química
de Catalunya,XTEC, Universitat Politècnica de Catalunya, Universitat
de Barcelona
|
   
Programació web: Xavier Jaén i Daniel Zaragoza.
Correcció lingüística: Serveis Linguïstics
de la Universitat Politècnica de Catalunya. |
Aquesta
obra està subjecta a una
Llicència
de Creative Commons

|
|
Recursos
de Física col·labora amb la
baldufa i també amb ciències
Revista del Professorat de Ciències de Primària i Secundària
(Edita: CRECIM-UAB)
|
|
|

 10/10
10/10 




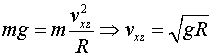
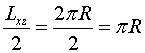 ,
el temps invertit serà:
,
el temps invertit serà: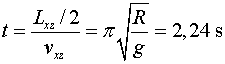

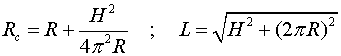
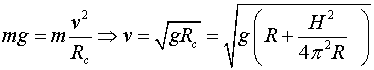

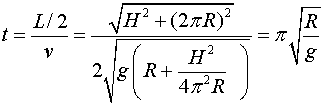
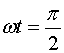 .
Prenent la normal nul·la tindrem
.
Prenent la normal nul·la tindrem