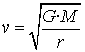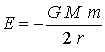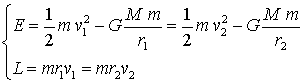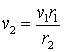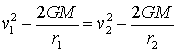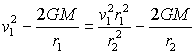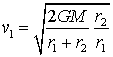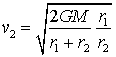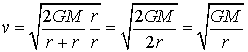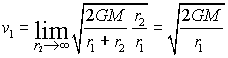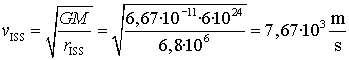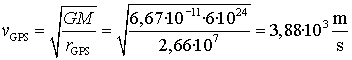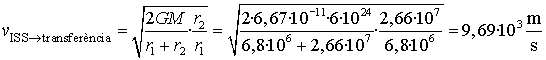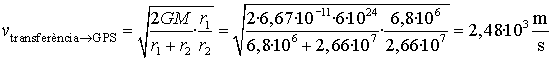Guia per al professoratIntroducció  
És fàcil arribar a calcular la velocitat que ha de mantenir un
satèl·lit (massa m)
en òrbita circular (radi r)
al voltant de la Terra (massa
M). Apliquem la segona llei de Newton i tenim en compte que, sobre
el satèl·lit, només hi actua la força gravitatòria,
que és la responsable de la seva acceleració centrípeta:
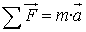
L'apliquem només en la component centrípeta
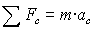
és a dir,
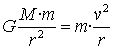
i després aïllem la velocitat
També és relativament senzill realitzar el càlcul de l'energia
d'un satèl·lit en òrbita circular (de radi r). Cal sumar l'energia
cinètica i la potencial gravitatòria:
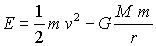
i substituint la velocitat per l'expressió (1) obtenim:
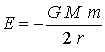
Paradoxa
És possible que alguna vegada ens haguem fet la pregunta,
o potser ens l'ha fet aquell alumne espavilat que sol fer preguntes “intel·ligents”:
Si un satèl·lit que està en òrbita
engega els coets propulsors, tot faria pensar que, en guanyar velocitat
i, per tant, augmentar l'energia, s'hauria d'allunyar de la Terra i, per
tant, hauria de passar a òrbites amb radis més grans. Però,
paradoxalment, comprovem que justament les òrbites més allunyades
de la Terra són les que tenen velocitats més petites (segons
l'expressió (1)).
Així doncs tenim una paradoxa que cal solucionar!
Solució
La solució és molt senzilla i podem explicar-la a l'alumnat
de batxillerat, tot i que els detalls dels càlculs numèrics
(no gaire complicats) queden fora del seu currículum. Vegem-ho.
Les fórmules que acabem de calcular i que solem aplicar en tots
els exercicis corresponen només a òrbites circulars malgrat
que sabem que la primera llei de Kepler diu que, en general, les òrbites
dels satèl·lits són el·líptiques. Així doncs
la solució a la nostra paradoxa és senzillament que el
satèl·lit que orbita amb velocitat vA
i que guanya velocitat (fins al valor veA
> vA) abandona l'òrbita circular i
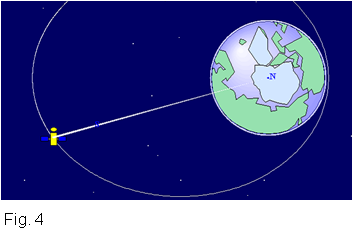
passar a orbitar en una el·lipse al voltant de la Terra (Figura 1).
Segons la segona llei de Kepler (Viquipèdia :
http://ca.wikipedia.org/wiki/Lleis_de_Kepler) , la velocitat d'un
planeta varia segons el punt de la trajectòria al voltant del
Sol: :
http://ca.wikipedia.org/wiki/Lleis_de_Kepler) , la velocitat d'un
planeta varia segons el punt de la trajectòria al voltant del
Sol:
El radi vector que uneix el planeta amb el Sol escombra àrees
iguals en temps iguals. Per tant, el planeta es desplaça
més ràpidament quan es troba en el periheli (punt
de l'òrbita situat a la mínima distància del
Sol) (veA)
que quan és en l'afeli (punt de l'òrbita situat a
la màxima distància del Sol) (veB).
|
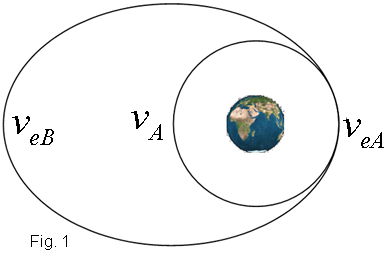 |
De manera que, tal com observem a la figura 2, veA
> veB.
Així doncs perquè un satèl·lit situat en una òrbita
circular (radi rA)
es pugui situar en una òrbita circular amb un radi més
gran (rB)
cal que recorri una òrbita de transferència el·líptica
amb una velocitat màxima (veA
) quan es troba a una distància rA
de la Terra i mínima (veB)
quan està a una distància rB.
El procés serà, doncs, el següent: el satèl·lit
orbita circularment (radi rA)
amb una velocitat vA
i cal que acceleri fins a obtenir una velocitat superior veA
que correspon a la velocitat del perigeu (punt de l'òrbita situat
a mínima distància de la Terra) de l'òrbita el·líptica
de transferència. Mentre recorre la trajectòria el·líptica
va disminuint la velocitat fins a arribar, just en l'apogeu (punt de
l'òrbita situat a la màxima distància), al valor
veB.
Aquesta disminució de velocitat es pot argumentar de forma senzilla,
tenint en compte que al llarg de la trajectòria, de A
fins a B,
el satèl·lit puja (s'allunya de la Terra). Just en aquest
moment (apogeu) ha de tornar a accelerar per augmentar la velocitat
fins a la velocitat vB
, que el situa a l'òrbita circular de radi rB.
Així doncs, la paradoxa és que el satèl·lit ha
d'augmentar dues vegades la seva velocitat per acabar en una òrbita
on la velocitat és inferior a la inicial. La segona llei de Kepler,
és a dir, la variació de la velocitat al llarg de la trajectòria
el·líptica, ens explica satisfactòriament la paradoxa.
Alguns càlculs
El càlcul de les velocitats en òrbites el·líptiques
és relativament fàcil, tot i que no s'inclou en el currículum
del batxillerat.
En el moviment d'un satèl·lit (òrbites circulars o el·líptiques)
s'han de conservar l'energia (E)
i també el moment angular (L).
Si escollim dos punts, 1 i 2, complint que el vector velocitat sigui
perpendicular al vector posició ( tal com es compleix en els
punts escollits de les trajectòries de la figura 2), tenim:
|
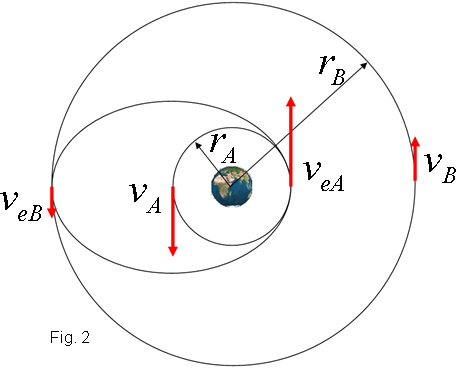 |
Tenint present que el concepte de moment angular no figura
en el currículum del batxillerat, per facilitar-ne la comprensió
a l'alumnat d'aquest nivell, en comptes de parlar de conservació de moment
angular podem igualar les dues àrees escombrades en el perigeu i en l'apogeu
de l'òrbita el·líptica, punts 1 i 2, tal com diu la segona
llei de Kepler o llei de les àrees (triangles amb una alçada r
i una base v dt,
on dt és
un diferencial de temps), que és conseqüència directa de
la conservació del moment angular:
A la igualtat (3) aïllem la velocitat
v2 :
Multipliquem per 2
la primera igualtat de (2) i després simplifiquem la massa m
del satèl·lit
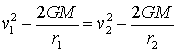
i substituïm v2
pel valor obtingut en l'expressió (3)
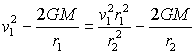
Amb alguns càlculs senzills, podem aïllar
v1 fins a obtenir l'expressió
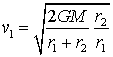
I utilitzant de nou l'expressió també obtenim el
valor de la velocitat v2
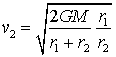
Podem comprovar que si l'òrbita és circular, és
a dir, r1=r2
aleshores obtenim en qualsevol de les dues fórmules la velocitat v
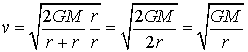
que coincideix amb l'expressió (1) que permet calcular
la velocitat orbital circular.
També podem comprovar que si l'òrbita no és tancada (en
el límit 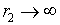 i v2=0)
obtenim l'expressió i v2=0)
obtenim l'expressió
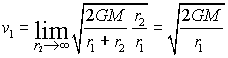
que correspon a la velocitat d'escapament d'una òrbita
circular.
Ara estem en condicions de resoldre numèricament algun exercici i comprovar-ho
amb alguna simulació.
Exercici  
Enunciat
La NASA vol situar un satèl·lit del sistema GPS en l'òrbita
correcta, però prèviament l'ha posat en l'òrbita de la
ISS (Estació Espacial Internacional) per efectuar-hi alguns ajustaments
en l'espai. Podeu calcular les velocitats orbitals i les velocitats que cal
comunicar al satèl·lit en els moments en què es fan les
transferències entre òrbites?
Solució
Primerament cal disposar de les dades de les òrbites, que podem trobar
a la Viquipèdia ( http://ca.wikipedia.org/wiki/GPS
i http://ca.wikipedia.org/wiki/GPS
i  http://ca.wikipedia.org/wiki/ISS) http://ca.wikipedia.org/wiki/ISS)
- GPS: h = 20200 km
- ISS: h = 400 km
(entre 370 i 460
km)
Així doncs, amb el radi de la Terra de 6400
km, els radis de les òrbites circulars seran:
- GPS: 26600 km
- ISS: 6800 km
Això ens permet calcular les velocitats de les òrbites circulars
de la ISS i del sistema GPS, suposant que massa del planeta és 6·1024
kg.
Nota: en els càlculs utilitzem sempre el sistema internacional
d'unitats (SI), de manera que les unitats dels resultats sempre han de ser les
corresponents a aquest sistema.
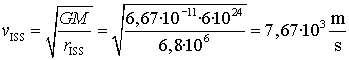
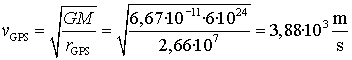
També podem obtenir les velocitats en el perigeu i en l'apogeu
de l'òrbita el·líptica de transferència.
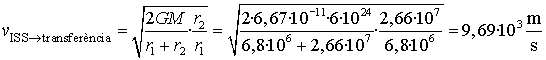
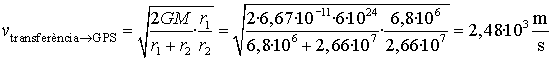
Simulacions
Podem utilitzar un parell de miniapliacions (applets) per simular
els moviments del satèl·lit i alhora comprovar que les
solucions són correctes.
Al web "Des simulations de sciences physiques pour vous cultiver
ou pour illustrer vos cours", del professor G. Gastebois, dintre
de l'apartat "Gravitation" podem trobar la miniaplicació
"Étude du mouvement (Satellites)". És recomanable
visualitzar-la amb una resolució alta de pantalla (1.280 x 1.024
o superior), sense les barres d'eines auxiliars del navegador (Preferits,
Històric...) i a pantalla completa (F11). (Fent clic a la figura
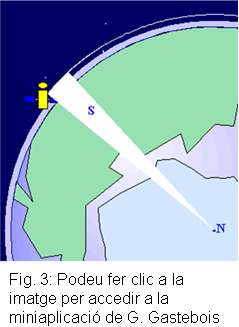
3 podeu accedir-hi directament.)
Per començar, podem triar l'opció “Satellite”
(apareix la Terra) i assignar als paràmetres superiors els valors
que corresponen a l'òrbita circular de la ISS:
En iniciar la simulació (botó inferior  ),
efectivament comprovarem que l'òrbita és circular i molt
propera al planeta (figura 3). Podem dur a terme altres observacions:
valor d'excentricitat molt petit, velocitat pràcticament constant,
la llei de les àrees de Kepler (botó inferior ),
efectivament comprovarem que l'òrbita és circular i molt
propera al planeta (figura 3). Podem dur a terme altres observacions:
valor d'excentricitat molt petit, velocitat pràcticament constant,
la llei de les àrees de Kepler (botó inferior )...
)...
|
 |
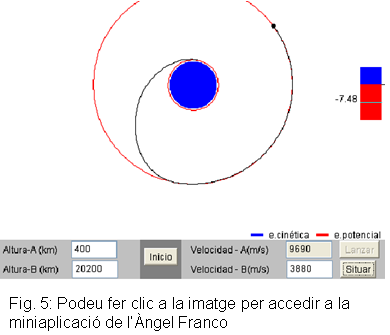
En el nostre cas, hi assignarem els valors:
En prémer el botó  ,
observarem les òrbites de la ISS i dels satèl·lits GPS.
|
 |
| Inici |
|
|
| ISSN:
1988-7930 Adreça a la xarxa:
www.RRFisica.cat Adreça electrònica:
redaccio@rrfisica.cat
difusio@rrfisica.cat
Comitè de redacció : Josep Ametlla, Octavi
Casellas, Xavier Jaén, Gemma Montanyà, Cristina Periago,
Octavi Plana, Jaume Pont i Ramon Sala.
Treballem conjuntament : Societat Catalana de Física,
Associació de Professores i Professors de Física i Química
de Catalunya,XTEC, Universitat Politècnica de Catalunya, Universitat
de Barcelona
|
   
Programació web: Xavier Jaén i Daniel Zaragoza.
Correcció lingüística: Serveis Linguïstics
de la Universitat Politècnica de Catalunya. |
Aquesta
obra està subjecta a una
Llicència
de Creative Commons

|
|
Recursos
de Física col·labora amb la
baldufa i també amb ciències
Revista del Professorat de Ciències de Primària i Secundària
(Edita: CRECIM-UAB)
|
|
|

 4/10
4/10 
 4/10
4/10