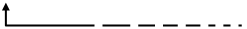núm 6 |
Tardor del 2010 |
Societat Catalana de Física |
| Inici |
| Sumari |   9/10 9/10  |
| El racó obscur Xavier Jaén |
|
| En un article d'aquest mateix número es parla de diamagnetisme i de levitació diamagnètica. És per això que dediquem “El racó obscur” a mirar d'esbrinar els fonaments del comportament magnètic de la matèria. Recordem que aquesta secció s’adreça principalment al professorat. Si, fruit d'aquest article, algun professor aprofita encara que sigui una petita part del que s'explica per a les seves classes, n'estarem més que contents! |
MagnetismesIntroduccióQuan una càrrega elèctrica es mou a una velocitat
Amb això ja podem donar per explicat el comportament
dels imants i dels materials que s’apropen? No, és clar. Al final
diem que tot és molt complex i, fins i tot, que l'origen del magnetisme
a la matèria té una arrel quàntica. La veritat és que hi ha molt pocs llibres de text, del nivell que sigui, que parlin de magnetisme a la matèria basant-se en la teoria més bàsica. Aquest fet fa que, tradicionalment, s'acabi associant el magnetisme a la matèria amb fenòmens més o menys obscurs en els quals la física quàntica té molt a veure, la qual cosa perpetua l'aura màgica que tradicionalment té el magnetisme. No ha estat senzill esbrinar què hi ha del cert en tot plegat, però espero haver aportat una mica de llum a aquest món màgic. Algunes de les qüestions a què fem referència són:
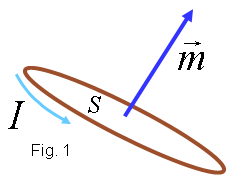
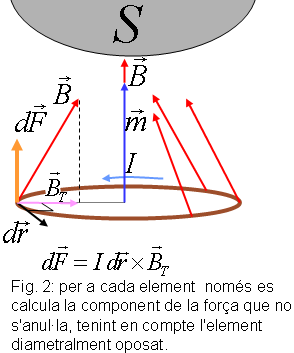
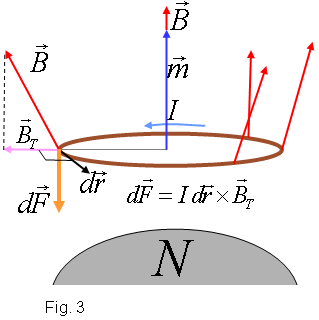
També cal dir que la motivació per escriure aquest Racó obscur prové de l'article Levitació diamagnètica de Marta Madrueño i Ferran Bertomeu, que es publica en aquest mateix número de Recursos de física. Acció d'un camp magnètic sobre una espira de corrent
La llei de FaradayLa llei de Faraday, tractada a El racó obscur del número 4, afirma que, si un camp magnètic variable en el temps travessa una espira, apareix un corrent amb un sentit que tendeix a anul•lar la variació de flux magnètic que el provoca. Aquí només volem recordar-la per deixar clar que, en principi, la llei de Faraday no té gaire relació amb el magnetisme a la matèria, ja que tracta amb camps magnètics variables en el temps. Les situacions en què els efectes magnètics ja es manifesten en la matèria no necessiten camps magnètics variables en el temps. Més d'un llibre esmenta els corrents induïts (deguts a la llei de Faraday(?)) per explicar l'efecte diamagnètic. Aquí no ho farem. Acció d'un camp magnètic sobre un sistema de càrregues en movimentAra no pensem en una espira sinó en un núvol
de N (
i=1...N
) càrregues iguals,
que podem escriure:
Si d'altra banda, féssim girar com un tot el sistema
de càrregues anterior, ara sense camp magnètic, amb una velocitat
angular
Si La matèriaLa matèria no és ben bé ni una espira
ni un núvol de partícules. La constitueixen àtoms, electrons
(partícules molt lleugeres amb càrrega negativa) que interactuen
amb un nucli (conglomerat de partícules relativament pesades de càrrega
positiva o neutra). Els moviments interns d'aquests àtoms no són,
en general, dissipatius. Un electró que dóna voltes al voltant
del nucli no hi frega ni hi troba cap resistència i, per tant, no s'atura.
Així, aquest electró es distingeix d'una espira macroscòpica
per la qual circula un corrent. El corrent d'una espira s'atura si no hi ha
cap generador que la mantingui, perquè hi ha resistència al seu
pas. Un electró no troba cap resistència, en un àtom. Efecte paramagnèticSuposem que els àtoms constituents d'un tros de matèria
tenen, per una causa o una altra, un moment magnètic Efecte diamagnèticSuposem que els àtoms constituents d'un tros de matèria
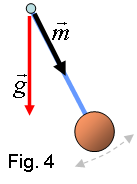
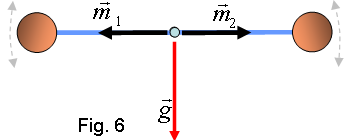
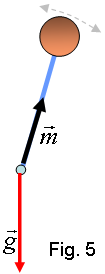
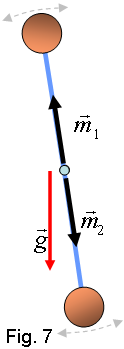
no tenen, per una causa o una altra, un moment magnètic Crec que sé el que esteu pensant. Ara aquest moment magnètic tendirà a alinear-se amb el camp, com passa en el cas de l'espira i del paramagnetisme. No defugirem aquesta possibilitat. Per això veurem un exemple molt més familiar, el d’uns pèndols sotmesos a un camp gravitatori uniforme.
Efecte ferromagnèticEn tot el que hem dit no hem fet intervenir la possible interacció magnètica entre àtoms. Quan dos o més moments magnètics es troben, tendeixen a alinear-se, però si no hi ha cap camp extern que els marqui una direcció preferent, l'agitació tèrmica s’encarrega de deixar les coses tal com estan. Si hi ha un camp magnètic que marca una direcció preferent i si, d'alguna manera, es dissipa energia, aquesta tendència a alinear-se arribarà fins al final: els dos moments magnètics acabaran alineats amb el camp magnètic i entre si, de manera que, quan retirem el camp magnètic, els moments magnètics seguiran alineats, ja que es reforçaran l'un a l'altre i l'agitació tèrmica pot no ser suficient per trencar aquest moment magnètic total. L'efecte global serà tenir un tros de matèria amb un moment magnètic global no nul. Tenim un imant! Aquest és l'efecte ferromagnètic. Fixem-nos que, com que el ferromagnetisme necessita algun efecte dissipatiu, sempre acabarà amb els moments magnètics en el mateix sentit que els camps. És per això que l'efecte ferromagnètic s'entén com un efecte paramagnètic límit. La diferència és que l'efecte paramagnètic desapareix en retirar el camp que l’ha provocat, ja que els moments magnètics no interactuen entre si i l'agitació tèrmica els desordena fàcilment; en canvi, en el cas ferromagnètic, aquesta agitació no és suficient per desordenar-los, ja que els àtoms estan alineats en una posició estable pel que fa a la interacció entre si. Substàncies paramagnètiques diamagnètiques i ferromagnètiquesTots aquests efectes es poden donar simultàniament en qualsevol tros de matèria. Depenent de les característiques, principalment atòmiques però també moleculars, etc., un efecte pot ser més important que els altres. Per això podem dir que hi ha substàncies paramagnètiques, diamagnètiques i ferromagnètiques. En termes generals, podem dir que l'efecte diamagnètic sempre existeix, però que queda encobert per l'efecte paramagnètic ( més intens) i encara més pel ferromagnètic (encara més intens), quan aquest hi són presents. Estabilitat de la levitació diamagnèticaEl que sorprèn més de la levitació diamagnètica
-i de l'ou com balla, tot sigui dit- és l'estabilitat amb què
es pot produir el fenomen. Estem acostumats al fet que els pols nord dels imants
es repel·leixin i facin un bot, girin tot encarant-se nord amb sud i,
finalment, s'enganxin. No podem aconseguir una configuració estable i
la levitació dels imants nord-nord és només un efecte transitori,
tret que no fem “trampes”, tal com els autors mostren a la figura
1 de l'article Levitació diamagnètica.
En canvi, en el cas diamagnètic, el tros de material no té tendència
a girar completament. Són els àtoms que oscil·len individualment,
de tal manera que el valor mitjà (espacial i temporal) del moment magnètic
té sentit contrari al camp magnètic. La força magnètica
apuntarà cap als llocs on B sigui mínim. Si només tenim
un imant, el tros de material serà escopit cap a fora..., però
si distribuïm els imants de manera que provoquem una zona de
|
|||||||||||||||||||||||||||||||||


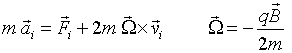
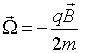 !
Aquest resultat constitueix el teorema de Larmor. Notem que la velocitat angular
!
Aquest resultat constitueix el teorema de Larmor. Notem que la velocitat angular