núm 7 |
Primavera del 2011 |
Societat Catalana de Física |
| Inici |
| Sumari |   3/9 3/9  |
| Interferències sonores Xavier Muñoz i Tavi Casellas |
|
| L’oïda és un òrgan sensitiu capaç de diferenciar diferents tipus de sons. Amb una educació musical adequada, podem arribar a apreciar els diferents harmònics que pot incloure la vibració d'una corda de violí. Fins i tot, els més erudits presumeixen que poden reconèixer la marca del violí que sona. Amb aquesta experiència no pretenem uns objectius tan ambiciosos, però sí que us oferim la possibilitat d’utilitzar l’oïda com a sensor per localitzar els punts d’interferència d’una ona sonora i, fins i tot, dibuixar les línies nodals. |
Guia del professorat
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
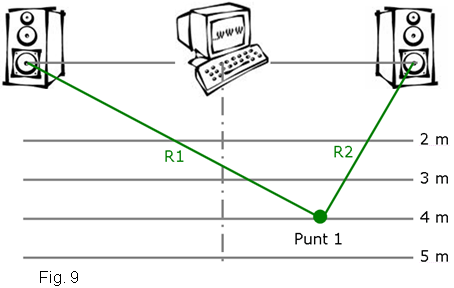
Amb l’ajuda de la cinta mètrica, dibuixarem al terra amb el guix blanc una paral•lela a la recta que uneix els dos altaveus i a una distància de 2 m, tal com es veu en la figura 8. Ens mourem al llarg de la paral•lela per tal de
determinar la posició dels punts d’interferència constructiva
i els marcarem amb el guix de color blau. En detectarem la localització
per la intensitat més elevada del so. Dibuixeu les línies nodals alineant els punts verds consecutius començant a partir de l’eix de simetria. Enumereu-les de forma simètrica: 1, 2 i 3.
|
 |
Dibuixeu també les línies d’interferència
constructiva alineant els punts blaus. La línia central (eix de simetria)
serà la línia zero i enumereu la resta de línies (de forma
simètrica): 1
i 2
Amb l’ajut de la cinta mètrica, determineu la distància
de tres punts de la línia d’interferència constructiva que
comença al mig dels altaveus. Seguiu aquest procediment per omplir la
taula de valors següent.
Qüestions
1) Amb l’ajut de la cinta mètrica, mesureu les
distàncies de tres punts de la línia d’interferència
constructiva 1. Seguiu
aquest procediment per omplir la taula de valors següent:
| Punts damunt la línia 1 | R1 (m) | R2 (m) | R1- R2 |
| Punt 1 |
|||
| Punt 2 |
|||
| Punt 3 |
2) Quin valor de R1-R2 esperaríeu trobar? Per què?
3) Què passa si us moveu per una línia nodal
qualsevol?
4) Què passa si us moveu per una línia d’interferència
constructiva?
5) Escolliu set punts situats damunt de les línies,
feu les mesures R1
i R2 als altaveus (tal com
s’observa en la figura 9) i ompliu la taula següent:
| Punts damunt la línia 1 | R1 (m) | R2 (m) | R1- R2 | 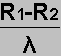 |
| Interferència constructiva central 0 |
||||
| Interferència constructiva 1 |
||||
| Interferència constructiva 2 |
||||
| R1 (m) | R2 (m) | R1- R2 | 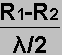 |
|
| Nodal 1
|
||||
| Nodal 1’
|
||||
| Nodal 2
|
||||
| Nodal 3 |
6) Sobre els valors de la darrera columna, comenteu quins serien
els valors esperats i quins són els resultats obtinguts. Expliqueu-ho
amb detall.
7) Si manteniu la distància entre els altaveus, pronostiqueu
un punt d’interferència constructiva i un de destructiva d’un
so que té una longitud d’ona de 3 metres. Verifiqueu la vostra
predicció amb el generador de sons.
8) Feu un esquema del resultat de l’experiència
anterior.
9) Compareu els resultats experimentals de la qüestió
6 amb els teòrics amb l’ajuda del simulador d’interferències
de FisLab.net. Intenteu justificar les diferències amb
les fonts d’error.
10) Segur que mai heu notat les interferències sonores
escoltant música, encara que ho hagueu fet amb un sistema de dos altaveus?
Expliqueu-ne el perquè.
11) Quin creieu que és el millor lloc (o millors llocs)
per escoltar música amb un sistema de dos altaveus? Justifiqueu la resposta.
12) Què creieu que passarà si la música
és en estèreo?

Solucions
Nota: Els valors següents es van obtenir en l’experiència feta per l’alumnat de segon de batxillerat de l’Institut Coll i Rodés de Lloret de Mar fent les interferències amb un so d’un metre de longitud d’ona.
1) Amb l’ajut de la cinta mètrica, mesureu les distàncies de tres punts de la línia d’interferència constructiva 1. Seguiu aquest procediment per omplir la taula de valors següent:
| Punts damunt la línia 1 | R1 (m) | R2 (m) | R1- R2 |
| Punt 1 |
3,30 | 2,00 | 1,30 |
| Punt 2 |
4,20 | 3,00 | 1,20 |
| Punt 3 |
5,20 | 4,00 | 1,20 |
2). Quin valor de R1-R2esperaríeu
trobar? Per què?
S’hauria d’obtenir sempre el valor 1 perquè,
com que estem situats sobre punts d’interferència constructiva,
la diferència de distàncies ha de ser un múltiple de la
longitud d’ona (valor unitari en aquest cas perquè estem situats
sobre la primera línia).
3) Què passa si us moveu per una línia nodal qualsevol?
Que pràcticament no sentim el so que generen
els altaveus a causa de la interferència destructiva (continuada al llarg
de tota la línia nodal).
4) Què passa si us moveu per una línia d’interferència constructiva?
En aquest cas sentim el so generat, la intensitat del
qual sempre es manté en un valor màxim.
5) Escolliu set punts situats damunt de les línies, feu les mesures R1 i R2 als altaveus (tal com s’observa en la figura 9) i ompliu la taula següent: :
| Punts damunt la línia 1 | R1 (m) | R2 (m) | R1- R2 | 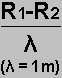 |
| Interferència constructiva central 0 |
2,60 |
2,60 |
0,00 |
0,00 |
| Interferència constructiva 1 |
3,25 |
2,20 |
1,05 |
1,05 |
| Interferència constructiva 2 |
4,15 |
1,95 |
2,20 |
2,20 |
| R1 (m) | R2 (m) | R1- R2 | 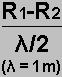 |
|
| Nodal 1
|
3,00 |
2,40 |
0,60 |
1,20 |
| Nodal 1’
|
2,40 |
3,00 |
-0,60 |
1,20 |
| Nodal 2
|
3,80 |
2,05 |
1,75 |
3,50 |
| Nodal 3 | 1,90 |
4,25 |
-2,35 |
4,70 |
6) Sobre els valors de la darrera columna, comenteu quins serien
els valors esperats i quins són els resultats obtinguts. Expliqueu-ho
amb detall.
A les tres primeres files hauríem de trobar els
valors teòrics 0,
1 i 2
que corresponen a desfasaments d’un nombre enter de longituds d’ona
i per tant es generen interferències constructives
A les files corresponents als nodes hauríem de trobar els valors 1,
3 i 5
que provoquen un desfasament de 180º
entre les dues ones (interferència destructiva).
Els valors obtinguts a partir de l’experiència s’aproximen
força als valors teòrics. Cal tenir en compte la dificultat que
suposa localitzar amb precisió els punts d’interferència
quan la oïda la tenim situada a uns 160
cm per damunt del terra.
7) Si manteniu la distància entre els altaveus, pronostiqueu un punt d’interferència constructiva i un de destructiva d’un so que té una longitud d’ona de 3 m. Verifiqueu la vostra predicció amb el generador de sons. Ens situem, per exemple, en un punt a 2
m metres d’un altaveu i a |
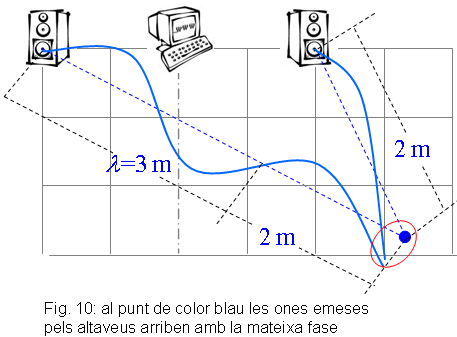 |
8) Feu un esquema del resultat de l’experiència anterior.
En l’esquema s’observa que el punt situat a 2 m d’un altaveu i a 5 m de l’altre, les dues ones arriben en fase (interferència constructiva).
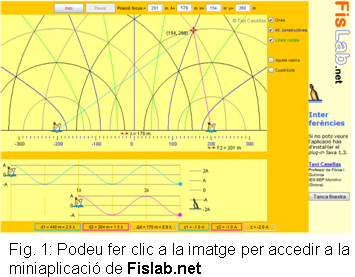
9) Compareu els resultats experimentals de la qüestió 6 amb els teòrics amb l’ajuda del simulador d’interferències de FisLab.net. Intenteu justificar les diferències amb les fonts d’error.
10) Segur que mai heu notat les interferències sonores escoltant música, encara que ho hagueu fet amb un sistema de dos altaveus? Expliqueu-ne el perquè.
La distribució i la quantitat de les línies
d’interferència depenen de la freqüència del so (o
la longitud d’ona). Com que la música correspon a una seqüència
de sons de diferents freqüències (i que canvia molt ràpidament),
un punt determinat de l’espai pot ser un node per a una freqüència
però un punt d’interferència constructiva per a un altre
so... i així contínuament.
11) Quin creieu que és el millor lloc (o millors llocs) per escoltar música amb un sistema de dos altaveus? Justifiqueu la vostra resposta.
Just en la línia de simetria (línia n=0)
sempre hi ha interferència constructiva (sigui quina sigui la longitud
d’ona) de manera que en qualsevol punt d’aquesta recta escoltarem
tots els sons amb una amplitud el doble de l’emesa per un dels altaveus.
En un punt d’aquesta línia mai no hi ha un node i, per tant, sentirem
perfectament bé totes les freqüències.
12) Què creieu que passarà si la música és en estèreo?
El so (la freqüència o longitud d’ona) emès per cada altaveu és diferent, per tant no podem aplicar res del que hem experimentat fins ara.

| Sumari |  3/9 3/9  |
| Inici | ||
| ISSN:
1988-7930 DL: B-31773-2012 Adreça a la xarxa:
www.RRFisica.cat Adreça electrònica:
redaccio@rrfisica.cat
difusio@rrfisica.cat |
||
  Programació web: Xavier Jaén i Daniel Zaragoza. Correcció lingüística: Serveis Linguïstics de la Universitat Politècnica de Catalunya. |
Aquesta
obra està subjecta a una Llicència de Creative Commons |
|
|
Recursos de Física col·labora amb la baldufa i també amb ciències Revista del Professorat de Ciències de Primària i Secundària (Edita: CRECIM-UAB) |
||



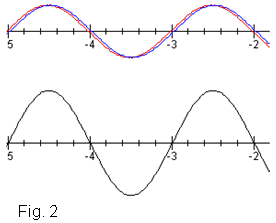




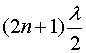 , on n
correspon al número de línia nodal (1,
2, 3...).
, on n
correspon al número de línia nodal (1,
2, 3...).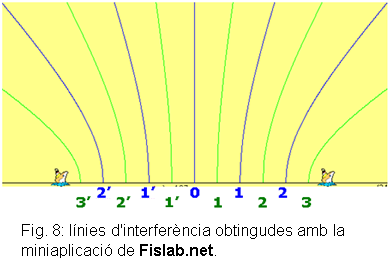
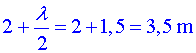 de l’altre. Les dues ones ens arriben desfasades mitja longitud
d’ona i per tant estarem en un node.
de l’altre. Les dues ones ens arriben desfasades mitja longitud
d’ona i per tant estarem en un node.