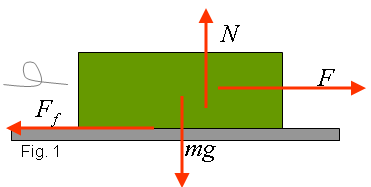
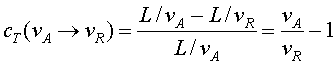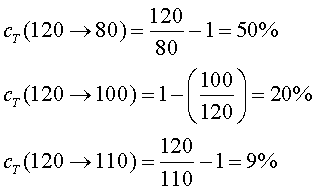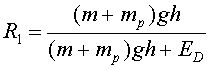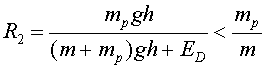La força del motor
Introducció
Molts cops quan plantegem situacions atractives
als estudiants posem exemples de cotxes, entre altres objectes. El problema
és que un cotxe no és un objecte inert. La causa del seu
moviment es troba dins d'ell mateix. Té un motor que provoca
forces internes que es transmeten a les rodes, etc. El cotxe finalment
es mou..., però què té a veure el model bloc amb
el del cotxe? El que volem analitzar en aquest article és com
podem descriure el moviment d'un cotxe i fins a quin punt podem mantenir
el model bloc. No volem donar a entendre que el que fem a continuació
pugi ser traslladat directament a l'estudiantat de batxillerat. Aquest
material pot servir per elaborar explicacions entenedores al nivell
adequat. El que no podem fer és mantenir el model bloc i no entendre
que un cotxe es mou perquè té un motor i gràcies,
també, a la fricció amb el terra!
|
 |
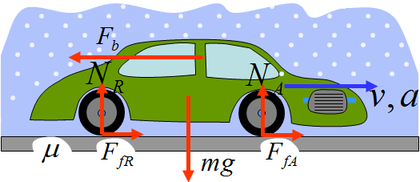
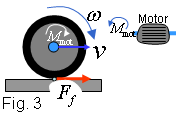
Del motor a les rodes
De les rodes al cotxe
Si tenim en compte que la força de fricció té
un valor màxim ,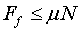 ,
obtenim un valor màxim per a l'acceleració: ,
obtenim un valor màxim per a l'acceleració:
Tenint en compte (1) i la condició de rodar sense lliscar,
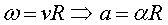 , si no volem que les
rodes es gastin inútilment el parell del motor no pot ser tan gran com
vulguem:
Normalment les rodes seran "petites". No necessàriament
petites de mida. Si tota la massa de la roda estigués a la perifèria
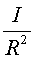 seria la seva massa.
Així, en general es complirà seria la seva massa.
Així, en general es complirà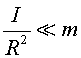 i tindrem
i tindrem 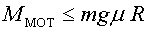 . .
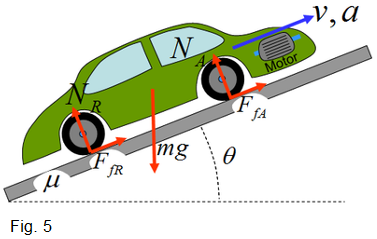
Si el cotxe ha de pujar per un pendent, obtenim resultats semblants
encara que més limitats (vegeu la figura 5):
|
 |
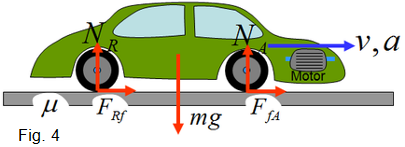
Tornant a la carretera horitzontal, si el cotxe ja ha accelerat
i no volem augmentar més la velocitat tindrem 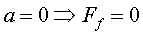 i també
i també 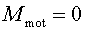 . La força
de fricció amb el terra no impedirà que el cotxe mantingui una
velocitat constant. Evidentment, sabem que en la pràctica això
no és així. Els dos motius més importants són: . La força
de fricció amb el terra no impedirà que el cotxe mantingui una
velocitat constant. Evidentment, sabem que en la pràctica això
no és així. Els dos motius més importants són:
- l'abonyegament del contacte neumàtic-terra fa aparèixer
una altra fricció que sí que s'oposa al moviment. Amb uns
neumàtics ben inflats i una carretera raonablement dura aquesta força
es pot minimitzar.
- El contacte entre la carrosseria del cotxe i l'aire provoca una fricció
aerodinàmica que, aquesta sí, és l'impediment més
important a l'avenç del cotxe. D'aquest en parlarem una mica més
endavant.
La conclusió que en podem treure és que la potència
del motor no farà l'efecte que volem si no tenim unes bones rodes. Un
motor "superpotent" no implica necessàriament que es puguin
fer canvis sobtats en la velocitat ni que es pugui pujar per qualsevol pendent.
Ara podeu entendre la dèria que tenen els de la fórmula 1, corbes
a part, amb els neumàtics.
Què passa amb l'energia?
Suposem que el cotxe va per una carretera plana i
va accelerant. Necessita les forces de fricció per fer-ho. Les
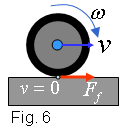
forces de fricció dissipen energia? El treball (infinitesimal)
d'una força és el producte d'aquesta pel desplaçament
del punt d'aplicació (vegeu la figura 6). El punt d'aplicació
de la força de fricció està al punt de la roda
en contacte amb el terra. Malgrat que el cotxe avança, aquest
punt no es mou! |
 |
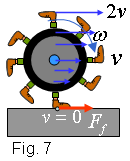
Per entendre aquesta subtilitat podem construir
un model de roda a base de peus (vegeu la figura 7). Si reduïm
el nombre de peus veurem que rodar és un cas extrem de caminar.
Quan caminem el peu que toca a terra està, mentre dura el contacte,
en repòs. Si augmentem el nombre de peus l'única cosa
que canvia és el lapse de temps en què un peu toca a terra,
però mentre toca a terra està en repòs! La conclusió
és que les forces de fricció degudes al contacte roda-terra
no treballen mentre la roda rodola per la carretera. |
 |
Així doncs, d'on prové l'energia que fa moure
el cotxe? Doncs del motor, és clar . La potència desenvolupada
pel motor lliurada a les rodes es pot calcular a partir del parell del motor
lliurat a cada roda i tenint en compte que tenim n
rodes motrius:
És a dir, si les rodes són "petites"
,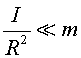 , la potència
del motor coincideix amb la que calcularíem sense cap mena de mirament
fent el producte de la força de fricció total , la potència
del motor coincideix amb la que calcularíem sense cap mena de mirament
fent el producte de la força de fricció total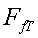 per la velocitat del cotxe. En aquest cas, estem pròxims al modeldel
bloc inert prenent com a força externa
per la velocitat del cotxe. En aquest cas, estem pròxims al modeldel
bloc inert prenent com a força externa 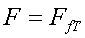 .
Cal tenir en compte que per a una piconadora, per exemple, això no seria
veritat. .
Cal tenir en compte que per a una piconadora, per exemple, això no seria
veritat.
I... què més passa amb l'energia?
Aquest curs, 2010-2011, hem viscut un encès
debat sobre la despesa energètica del cotxes. És interessant
posar-hi cullerada amb les eines que tenim a l'abast.
Centrem la situació en la circulació
d'un cotxe per una carretera horitzontal. Si no hi hagués cap
altra fricció més que la de la carretera, necessària
per accelerar, girar, etc., no hi hauria cap problema, ja que un cop
aconseguida la velocitat a què volem arribar la despesa energètica
seria nul·la. En aquestes condicions l'única despesa energètica
es dóna en frenar (fricció dissipativa de debò
en els cotxes actuals) i en accelerar (que mai serà nul·la i
dependrà del rendiment del motor). Per això, un primer
consell és no anar canviant de velocitat constantment i sense
motiu.
Introduïm ara la força de fricció aerodinàmica
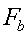 (vegeu la figura
8). Estudiarem el cas en què el cotxe viatja a velocitat constant.
Ara caldrà una despesa energètica per mantenir aquesta
velocitat: (vegeu la figura
8). Estudiarem el cas en què el cotxe viatja a velocitat constant.
Ara caldrà una despesa energètica per mantenir aquesta
velocitat: |
|
Si per simplificar fem servir l'aproximació de roda
petita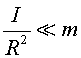 , tenim , tenim
Tota aquesta potència es dissipa a través de
la fricció aerodinàmica. Posem-ne un exemple: comparem la potència
consumida pel motor a una velocitat donada, en direm velocitat Actual,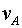 ,
i a una velocitat Restringida ,
i a una velocitat Restringida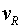 .
L'estalvi relatiu de Potència, .
L'estalvi relatiu de Potència, 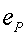 ,
és ,
és
Podem posar alguns exemples d'estalvi de potència molt
discutits el curs 2010-2011 per les autoritats de trànsit i altre que
no hi tenen competències:
Els estalvis de potència són realment espectaculars!
Hom pot però esgrimir l'argument que si vaig més a poc a poc també
trigaré més. És veritat. Així que centrem-nos en
un recorregut horitzontal concret 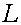 fet
a una velocitat constant fet
a una velocitat constant 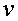 .
Tenim .
Tenim 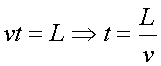
La despesa energètica per fer aquest recorregut serà
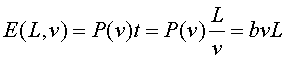 , i l'estalvi
relatiu Energètic, , i l'estalvi
relatiu Energètic,  ,
si passem d'anar d'una velocitat ,
si passem d'anar d'una velocitat  a
a 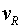 : :
Posem els mateixos exemples:
Encara paga la pena. Hom encara pot esgrimir un altre argument.
Si vaig més lent trigaré més... i segons com deixaré
de guanyar-hi diners. Mirem d'avaluar el consum relatiu de
Temps 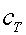 . .
El temps que trigo a fer el recorregut 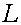 a la velocitat
a la velocitat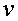 és és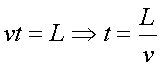 .
El temps consumit si passem d'anar a .
El temps consumit si passem d'anar a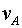 a
a 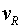 : :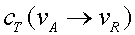 és és
Analitzant els mateixos exemples:
Suposem que el temps me'l paguen a preu de combustible. És
a dir que si anar a una certa potència em costa x
euros per unitat de temps llavors per cada unitat de temps podria guanyar x
euros. Podem interpretar els %
de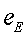 i i 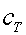 en termes de diners estalviats i perduts. Hi ha manera d'estalviar més
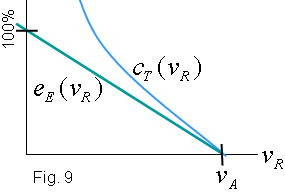
energia (diners) del que consumim en temps (diners)? Doncs no. Les gràfiques
(vegeu la figura 9) indiquen que no és possible trobar, a partir d'una
velocitat actual
en termes de diners estalviats i perduts. Hi ha manera d'estalviar més
energia (diners) del que consumim en temps (diners)? Doncs no. Les gràfiques
(vegeu la figura 9) indiquen que no és possible trobar, a partir d'una
velocitat actual 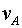 ,
una de restringida ,
una de restringida 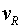 de
manera que el consum de temps no superi l'estalvi energètic. de
manera que el consum de temps no superi l'estalvi energètic.
A partir d'aquí comencem a veure que el problema no
és només físic. En les comparacions precedents hem interpretat
que en el temps que es triga de més es deixen de guanyar diners al mateix
ritme que el que hom s'estalvia en combustible. En general això no és
cert. És més, a vegades cal anar ràpid i no pas per diners,
com és el cas d'una ambulància! Però per a la majoria de
nosaltres, quan utilitzem el cotxe per anar a fer la costellada del diumenge,
el temps guanyat no ens fa guanyar més diners. De fet, el que acaba determinant
el temps que es triga és, cues a part, la distància.
Possiblement és per aquí per on es pot atacar el problema. Com
que cada cop anem a fer la costellada més lluny, cada cop tenim la necessitat
d'anar més ràpid per perdre, si més no, el mateix
temps... Tot plegat, un desastre, perquè cada cop contaminem
més, ja que si finalment el que fixem és el temps, el càlcul
que s'ajusta més és el que expressen les relacions (11).
Però ja es veu que, malgrat que els càlculs els tenim al davant,
la discussió pot ser molt llarga.
| Ara, si pensem una mica més, un rendiment,
encara que sigui energètic, és el quocient, en termes
d'energia, entre el que volem aconseguir i la despesa necessària
per aconseguir-ho. El cotxe no és aquí un fi en si mateix,
és la màquina que ens permet aconseguir el que volem.
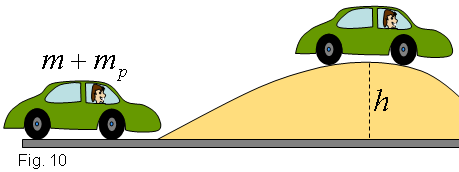
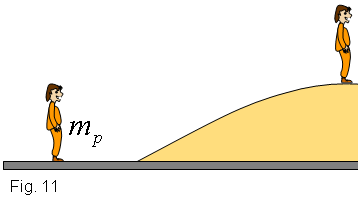
Si el que vol el noi de la figura 11 és pujar la muntanya, una
de les maneres de fer-ho és utilitzar un cotxe. Però recordem
que l'objectiu del noi no és pujar amb el cotxe a d'alt de la
muntanya. El rendiment del cotxe és, en aquest cas:
Aquest rendiment, per més que rebaixem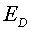 ,
no podrà mai superar ,
no podrà mai superar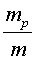 .
Si l'objectiu és només pujar el noi, d'uns 70
kg , amb un cotxe d'uns 1400
kg, és un rendiment que, com a màxim, arriba al
5%.
Si en l'operació s'aprofita per pujar quatre persones,
amb una massa semblant, el grau màxim del rendiment augmenta
fins a un 20%. .
Si l'objectiu és només pujar el noi, d'uns 70
kg , amb un cotxe d'uns 1400
kg, és un rendiment que, com a màxim, arriba al
5%.
Si en l'operació s'aprofita per pujar quatre persones,
amb una massa semblant, el grau màxim del rendiment augmenta
fins a un 20%.
La rebaixa en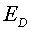 continua
sent important ja que acostuma a anar lligada a la rebaixa de contaminants. continua
sent important ja que acostuma a anar lligada a la rebaixa de contaminants. |
 |

|

 9/9
9/9 



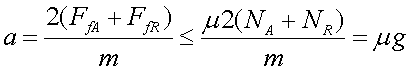
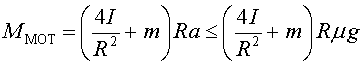
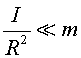 i tindrem
i tindrem 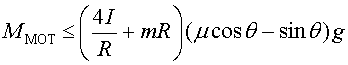



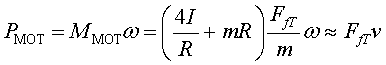

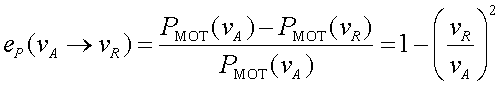
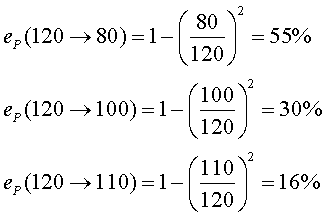
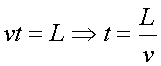
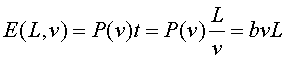 , i l'estalvi
relatiu Energètic,
, i l'estalvi
relatiu Energètic, 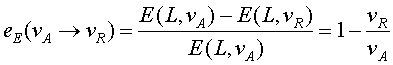
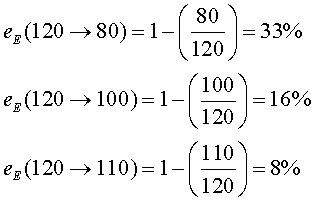
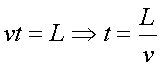 .
El temps consumit si passem d'anar a
.
El temps consumit si passem d'anar a