Guia per al professorat
Es tracta de dues activitats sobre la relativitat del temps. La
primera es basa en la lectura d’una petita història o conte en
què s’explica la dilatació del temps si fóssim capaços
de viatjar a velocitats properes a la de la llum.
Recordeu que a El racó Obscur  (primavera de2010) ja es tractà aquest tema. La segona activitat és
una demostració d’aquesta relativitat en el comportament dels muons,
que provenen dels raigs còsmics, quan arriben a la superfície
de la Terra.
(primavera de2010) ja es tractà aquest tema. La segona activitat és
una demostració d’aquesta relativitat en el comportament dels muons,
que provenen dels raigs còsmics, quan arriben a la superfície
de la Terra.
Temporalització
Tres classes. Una d’explicació de la teoria (amb la lectura del
conte), una altra de càlculs i plantejament d’uns exercicis, i
una tercera podria ser de resolució conjunta dels exercicis o qüestions
proposades.
Alumnes als quals s’adreça l’experiència
2n de batxillerat, quan s’estudien els temes relacionats
amb la nova física.
El conte dels bessons. Full de l’alumnat
Objectiu
 Comprendre la relativitat del temps. Comprendre la relativitat del temps.
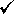 Veure que no es tracta de ciència-ficció,
sinó d’una cosa que és real i experimental. Veure que no es tracta de ciència-ficció,
sinó d’una cosa que és real i experimental.
Conte
| En Joan i l’Ester
són una parella de 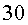 anys. Tenen dos fills bessons: l’Alba i en Roger. Els dos joves
pares són científics i han construït una nau de dues
places capaç de viatjar a velocitats molt properes a la de la llum.En
el moment en què els seus dos fills van complir un any, els dos
científics van decidir experimentar amb la seva nau. Viatjarien
durant
anys. Tenen dos fills bessons: l’Alba i en Roger. Els dos joves
pares són científics i han construït una nau de dues
places capaç de viatjar a velocitats molt properes a la de la llum.En
el moment en què els seus dos fills van complir un any, els dos
científics van decidir experimentar amb la seva nau. Viatjarien
durant 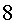 anys, anys,
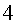 d’anada
i d’anada
i 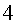 de tornada.
L’objectiu del viatge seria doble: d'una banda, intentar arribar
molt prop de l’estrella Alfa de la constel·lació del
Centaure, que és la més propera a la Terra. De l'altra,
experimentar quins problemes de salut podrien trobar-se en un viatge d’aquestes
característiques. Decidiren que serien l’Ester i en Roger,
els que hi embarcarien, per retornar al cap de 8 anys amb moltes dades
d’investigació espacial i biològica. En Joan i l’Alba
els estarien esperant. I així es va fer. de tornada.
L’objectiu del viatge seria doble: d'una banda, intentar arribar
molt prop de l’estrella Alfa de la constel·lació del
Centaure, que és la més propera a la Terra. De l'altra,
experimentar quins problemes de salut podrien trobar-se en un viatge d’aquestes
característiques. Decidiren que serien l’Ester i en Roger,
els que hi embarcarien, per retornar al cap de 8 anys amb moltes dades
d’investigació espacial i biològica. En Joan i l’Alba
els estarien esperant. I així es va fer.
L’Ester va programar per a la nau una velocitat de 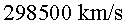 .
Amb .
Amb 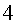 anys havien
d’arribar a una distància de anys havien
d’arribar a una distància de 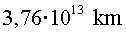 .
L’estrella Alfa Centauri és a .
L’estrella Alfa Centauri és a 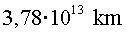 .
Per tant la podrien observar relativament de prop. .
Per tant la podrien observar relativament de prop.
Van passar 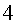 anys
a la nau. El mateix dia que en Roger celebrava amb la seva mare el cinquè
aniversari, ella va mirar el comptador de quilòmetres de la nau.
Marcava anys
a la nau. El mateix dia que en Roger celebrava amb la seva mare el cinquè
aniversari, ella va mirar el comptador de quilòmetres de la nau.
Marcava 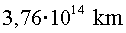 i no
hi havia cap rastre d’Alpha. L’Ester va revisar-ho tot i va
comprovar que tot era correcte. Va fer un senzill càlcul: i no
hi havia cap rastre d’Alpha. L’Ester va revisar-ho tot i va
comprovar que tot era correcte. Va fer un senzill càlcul:
- Si hem recorregut 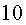 vegades més del que estava programat en
vegades més del que estava programat en 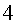 anys, la nostra velocitat ha estat
anys, la nostra velocitat ha estat 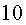 vegades
més gran que la que prevèiem; per tant, només hi
ha una conclusió: la teoria de la relativitat d’Einstein
és equivocada. vegades
més gran que la que prevèiem; per tant, només hi
ha una conclusió: la teoria de la relativitat d’Einstein
és equivocada. |
 |
Fig. 1: Albert Einstein 
(14 de març del 1879 - 18 d'abril del 1955) va ser un físic
d'origen alemany, nacionalitzat posteriorment suís i estatunidenc.
És el científic més conegut i important del segle
XX. La foto de la figura va ser feta en una visita realitzada a Barcelona
l'any1923. |
| Ella i el seu
fill havien aconseguit viatjar a 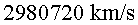 ,
és a ddir, ,
és a ddir, 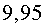 vegades més ràpid que la llum !!! Aquesta proesa era el
millor regal que li podia fer al seu fill Roger de
vegades més ràpid que la llum !!! Aquesta proesa era el
millor regal que li podia fer al seu fill Roger de 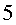 anys. Molt contenta, es disposà a viatjar de tornada cap a la Terra.
D’altra banda, no van experimentar cap dificultat de tipus biològic,
raó per la qual en arribar a la Terra tindrien moltes coses per
celebrar.
anys. Molt contenta, es disposà a viatjar de tornada cap a la Terra.
D’altra banda, no van experimentar cap dificultat de tipus biològic,
raó per la qual en arribar a la Terra tindrien moltes coses per
celebrar.
Passats 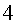 anys
més a la nau, van arribar a la Terra. Però ningú
feia cas dels seus senyals de ràdio quan ja hi estaven a molt poca
distància. La nau aterrà en un gran descampat. No hi havia
ningú, però a prop veieren una carretera i s’hi quedaren
esperant que passés algun cotxe. Era el dia del novè aniversari
d’en Roger. L’Ester li digué: anys
més a la nau, van arribar a la Terra. Però ningú
feia cas dels seus senyals de ràdio quan ja hi estaven a molt poca
distància. La nau aterrà en un gran descampat. No hi havia
ningú, però a prop veieren una carretera i s’hi quedaren
esperant que passés algun cotxe. Era el dia del novè aniversari
d’en Roger. L’Ester li digué:
- Roger, ben aviat celebrarem tots junts i a casa
el teu aniversari, els teus 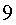 anys, i el de la teva germaneta Alba, de qui tantes vegades t’he
parlat durant el viatge.
anys, i el de la teva germaneta Alba, de qui tantes vegades t’he
parlat durant el viatge.
Mentre deia això, un cotxe es va parar. Van saber
que es trobaven molt prop de la ciutat on vivien.
|
 |
Fig. 1: El físic francès Paul Langevin 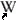
((París, 1872 - 1946) ) il·lustrà, amb la paradoxa
dels bessons, l'existència de temps diferents en funció
de la velocitat, una velocitat que dilata el temps. |
| A mesura que
s’anaven acostant a la ciutat, l’Ester estava inquieta en
no reconèixer res. No semblava pas que fos casa seva, aquella ciutat.
El conductor els va ratificar que era el lloc on anaven. L’Ester
va començar a pensar i a lligar caps: el cotxe era molt estrany,
la manera de vestir del conductor també i el lloc estava molt canviat.
Mentre anava pensant tot això, va veure un calendari dins el cotxe.
Marcava l’any 2090!.
Ella havia sortit de la Terra l’any 2010
! No podia ser!
Arribaren a la ciutat i en baixar del cotxe l’Ester, molt nerviosa,
va començar a buscar el carrer on vivien. Un cop arribats, va veure
que tot estava molt canviat. Va trobar la porta del que creia que era
casa seva i hi va trucar. Uns senyora de mitjana edat va obrir . L’Ester
es va identificar però la senyora no va entendre res; només
li va donar el nom de la persona que li havia venut aquella casa: una
anciana de 81 anys que es deia Alba i que ara vivia davant mateix, a l’altre
costat del carrer.
A l’Ester se li va glaçar la sang! Va mirar el seu fillet
de 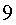 anys i li
va dir: anys i li
va dir:
- Perdona’m fill, la teva mare ha estat massa
orgullosa. Einstein tenia raó. No es pot sobrepassar la
velocitat de la llum. He fracassat!
En Roger no entenia res.
Van passar a l’altra banda del carrer i van trucar a la porta indicada.
Una senyora gran de 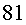 anys
els va rebre i els va conèixer. Era l’Alba, la germana bessona
d’en Roger. El seu pare, en Joan, li havia parlat del seu germà
i de la seva mare. I en el seu moment, quan va reconèixer l’error
que havien comès i abans de morir, li va dir que els esperés.
L’anciana filla i la jove mare es van abraçar. El pare mort;
la filla Alba de anys
els va rebre i els va conèixer. Era l’Alba, la germana bessona
d’en Roger. El seu pare, en Joan, li havia parlat del seu germà
i de la seva mare. I en el seu moment, quan va reconèixer l’error
que havien comès i abans de morir, li va dir que els esperés.
L’anciana filla i la jove mare es van abraçar. El pare mort;
la filla Alba de 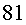 anys, la seva mare; l’Ester, de
anys, la seva mare; l’Ester, de 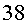 ,
i l’altre fill, germà de l’Alba, en Roger, de ,
i l’altre fill, germà de l’Alba, en Roger, de 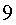 anys van ser tots víctimes de la dilatació del temps.
anys van ser tots víctimes de la dilatació del temps.
|
 |
Fig. 1:La teoria de la relativitat va tenir i té
una forta influència en tots els àmbits de la societat.
La persistència de la memòria, popularment coneguda
com Els rellotges tous, és una de les més reconegudes
obres de Salvador Dalí 
(Figueres, 11 de maig de 1904 – íbidem, 23 de gener de
1989). Es tracta d'un oli sobre tela de 24 x 33 cm que l'artista empordanès
pintà el 1931. |
Explicació
Explicació científica del conte.
La teoria de la relativitat d’Einstein postula que la
velocitat de la llum en el buit és una constant universal que no es pot
sobrepassar. És com un límit de velocitats, totalment independent
del sistema de referència: no podem ni sumar-la ni restar-la a cap altra
velocitat. Això implica forçosament que el temps deixa de ser
un concepte absolut. Com transcorre el temps depèn del nostre estat de
moviment. Això no ho notem respecte a nosaltres mateixos, és clar.
Però sí que es nota en comparar els temps transcorreguts.
Considerem dues persones, una en repòs i l'altra que
viatja a velocitat de mòdul constant 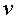 respecte
de la primera. A cada una de les persones els passa el temps, el seu temps.
Si no es tornen a trobar mai més, no tindrà sentit que comparem
els temps que els passa a l’una i l'altra, però sí si la
que viatja torna. Notem que pot tornar mantenint el mòdul de la velocitat
constant, però necessariament haurà d'accelerar en fer el viratge!
Un observador inercial és una persona que està en repòs
o viatja a velocitat (mòdul, direcció i sentit) constant. Només
la persona que resta en repòs es pot considerar que és un observador
inercial; no la que viatja. respecte
de la primera. A cada una de les persones els passa el temps, el seu temps.
Si no es tornen a trobar mai més, no tindrà sentit que comparem
els temps que els passa a l’una i l'altra, però sí si la
que viatja torna. Notem que pot tornar mantenint el mòdul de la velocitat
constant, però necessariament haurà d'accelerar en fer el viratge!
Un observador inercial és una persona que està en repòs
o viatja a velocitat (mòdul, direcció i sentit) constant. Només
la persona que resta en repòs es pot considerar que és un observador
inercial; no la que viatja.
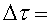 és el temps
transcorregut que mesura la persona en moviment, la que viatja a una certa velocitat és el temps
transcorregut que mesura la persona en moviment, la que viatja a una certa velocitat
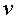 i després torna.
S'anomena temps propi. i després torna.
S'anomena temps propi.
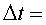 és el temps
transcorregut que mesura la persona en repòs. És també
el seu temps propi. és el temps
transcorregut que mesura la persona en repòs. És també
el seu temps propi.
Segons la relativitat, podem escriure que
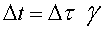
on 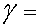 és
la correcció relativista és
la correcció relativista
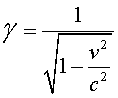
on 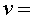 és el mòdul
constant de la velocitat a què es viatja i és el mòdul
constant de la velocitat a què es viatja i 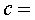 és la velocitat de la llum en el buit
és la velocitat de la llum en el buit 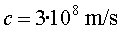 . .
En el cas del nostre conte,
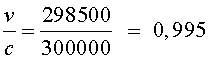
Fent els càlculs, tenim que 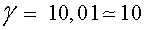 (
farem servir el valor aproximat (
farem servir el valor aproximat 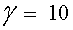 ). ).
Això vol dir que si la persona que viatja torna al cap de 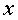 anys (mesurats segons els seus rellotges), el temps que hauria transcorregut
segons els rellotges de la persona que resta en repòs seria de
anys (mesurats segons els seus rellotges), el temps que hauria transcorregut
segons els rellotges de la persona que resta en repòs seria de 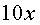 anys!. anys!.
En el conte, l’Ester, de 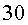 anys
i en Roger, d’ anys
i en Roger, d’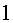 any, han estat viatjant, segons ells mateixos,
any, han estat viatjant, segons ells mateixos, 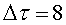 anys a aquesta velocitat
anys a aquesta velocitat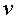 .
Per tant, en retornar a la Terra l’Ester té .
Per tant, en retornar a la Terra l’Ester té 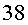 anys i en Roger en té
anys i en Roger en té 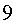 . .
Però quan l'Ester i en Roger arriben del viatge, el temps transcorregut
per a l'Alba i en Joan, en repòs a la Terra, respecte de la qual la nau
ha viatjat a la velocitat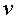 ,
serà ,
serà  . El Joan
que tenia . El Joan
que tenia 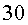 anys, ara
en tindria anys, ara
en tindria 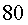 més, més,
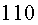 , i ja és mort.
La seva filla Alba, d’ , i ja és mort.
La seva filla Alba, d’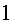 any, ara en té
any, ara en té 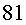 . .
Pel que fa al fet d’anar a l’estrella Alfa, és evident que
van arribar 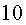 vegades
més lluny a causa que els temps de durada del viatge estaven calculats
segons els temps transcorreguts a la Terra. Per tant, es tracta de temps vegades
més lluny a causa que els temps de durada del viatge estaven calculats
segons els temps transcorreguts a la Terra. Per tant, es tracta de temps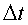 ; però a la nau el temps que es mesura és el temps propi
; però a la nau el temps que es mesura és el temps propi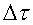 .
Haurien d’haver comptat amb la relativitat del temps. Si ho haguessin
fet, tenint el compte la teoria de la relativitat, haurien arribat a Alfa, segons
els rellotges de la nau, en .
Haurien d’haver comptat amb la relativitat del temps. Si ho haguessin
fet, tenint el compte la teoria de la relativitat, haurien arribat a Alfa, segons
els rellotges de la nau, en 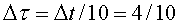 anys,
és a dir, en anys,
és a dir, en  dies. El seu viatge d’anada i tornada només hauria durat, segons
els rellotges de la nau,
dies. El seu viatge d’anada i tornada només hauria durat, segons
els rellotges de la nau, 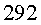 dies. Quan haguessin tornat a la Terra, l’Ester encara no hauria tingut
els
dies. Quan haguessin tornat a la Terra, l’Ester encara no hauria tingut
els 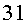 i en Roger encara
no hauria tingut els i en Roger encara
no hauria tingut els 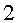 anys. El seu marit Joan hauria tingut
anys. El seu marit Joan hauria tingut 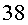 anys.I la germana bessona, l’Alba, n’hauria tingut, encara,
anys.I la germana bessona, l’Alba, n’hauria tingut, encara, 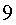 . .
Qüestionari
 Primera qüestió:
Primera qüestió:
Per allunyar-se de la Terra i vèncer el camp gravitatori fa falta una
velocitat de 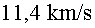 , coneguda
com a velocitat d’escapament. Quan es viatja a aquesta velocitat, es produeix
algun canvi en els rellotges? És a dir, es produeix alguna dilatació
del temps? Si viatgéssim a aquesta velocitat, quant de temps trigaríem
a arribar a Alfa Centauri ? , coneguda
com a velocitat d’escapament. Quan es viatja a aquesta velocitat, es produeix
algun canvi en els rellotges? És a dir, es produeix alguna dilatació
del temps? Si viatgéssim a aquesta velocitat, quant de temps trigaríem
a arribar a Alfa Centauri ?
 Segona
qüestió: Segona
qüestió:
Imaginem un enorme tren (de milers de quilòmetres de llarg) que es mou
a la mateixa velocitat de la nau de l’Ester, que hi va a dintre. Imaginem
que en Joan veu passar el tren davant seu i pot observar el que hi passa a dintre.
L’Ester enfoca una llanterna al sostre del tren, on hi ha un mirall. Ella
veu que la llum hi arriba i en torna verticalment. En Joan veu que la llum segueix
el camí d’un triangle isòsceles i tarda 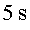 a arribar al mirall i
a arribar al mirall i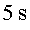 més a tornar al terra.
més a tornar al terra.
Calculeu:
a) L’alçada del tren, tenint en compte que en
Joan veu que la llum viatja durant 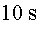 i que el tren va a
i que el tren va a 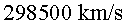 .
Per fer-ho, apliqueu-hi raonaments geomètrics. L’alçada
del vagó del tren és tremenda. Penseu que és un tren imaginari! .
Per fer-ho, apliqueu-hi raonaments geomètrics. L’alçada
del vagó del tren és tremenda. Penseu que és un tren imaginari!
b) El temps que l’Ester, a dalt del vagó, veurà
la llum viatjant.
c) L’Ester i en Joan no es posen d’acord amb la
trajectòria que segueix la llum. Qui té raó? Pel que fa
al temps que tarda la llum a fer el recorregut, també depèn de
l’observador. Es compleix la teoria de la relativitat?
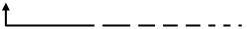
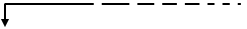 
El conte dels bessons. Solucions
 Primera
qüestió: Primera
qüestió:
Per allunyar-se de la Terra i vèncer el camp gravitatori fa falta una
velocitat de 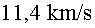 , coneguda
com a velocitat d’escapament. Quan es viatja a aquesta velocitat, es produeix
algun canvi en els rellotges? És a dir, es produeix alguna dilatació
del temps? Si viatgéssim a aquesta velocitat, quant de temps trigaríem
a arribar a Alfa Centauri ? , coneguda
com a velocitat d’escapament. Quan es viatja a aquesta velocitat, es produeix
algun canvi en els rellotges? És a dir, es produeix alguna dilatació
del temps? Si viatgéssim a aquesta velocitat, quant de temps trigaríem
a arribar a Alfa Centauri ?
Imaginem que l’Ester viatja amb la nau a una velocitat
de 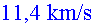 . Calculem . Calculem . .
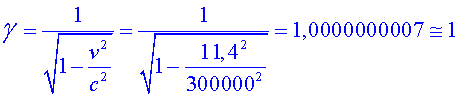
Per tant, no hi ha cap dilatació.
Però si viatgen a aquesta velocitat cap a Alfa Centauri, a 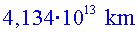 ,
el temps que triguen a arribar-hi és ,
el temps que triguen a arribar-hi és
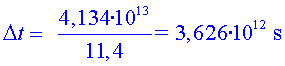
Si dividim el resultat per 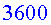 ,
per passar-ho a hores, després per ,
per passar-ho a hores, després per 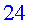 ,
per passar-ho a dies, i després per ,
per passar-ho a dies, i després per 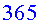 ,
per passar-ho a anys, trobem un temps d’anada de ,
per passar-ho a anys, trobem un temps d’anada de 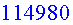 anys.
anys.
Si comptem l’anada i la tornada serien 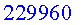 anys! anys!
Potser seria millor considerar la dilatació del temps i poder viatjar
a velocitats relativistes.
 Segona
qüestió: Segona
qüestió:
Imaginem un enorme tren (de milers de quilòmetres de llarg) que es mou
a la mateixa velocitat de la nau de l’Ester, que hi va a dintre. Imaginem
que en Joan veu passar el tren davant seu i pot observar el que hi passa a dintre.
L’Ester enfoca una llanterna al sostre del tren, on hi ha un mirall. Ella
veu que la llum hi arriba i en torna verticalment. En Joan veu que la llum segueix
el camí d’un triangle isòsceles i tarda 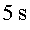 a arribar al mirall i
a arribar al mirall i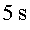 més a tornar al terra.
més a tornar al terra.
Calculeu:
a) L’alçada del tren, tenint en compte que en
Joan veu que la llum viatja durant 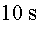 i que el tren va a
i que el tren va a 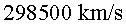 .
Per fer-ho, apliqueu-hi raonaments geomètrics. L’alçada
del vagó del tren és tremenda. Penseu que és un tren imaginari! .
Per fer-ho, apliqueu-hi raonaments geomètrics. L’alçada
del vagó del tren és tremenda. Penseu que és un tren imaginari!
Mireu el dibuix.
En Joan, que ho veu tot des de fora veu com la llum tarda 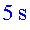 i
i 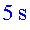 més a reflectir-se
en el mirall. (va d’ més a reflectir-se
en el mirall. (va d’ 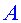 cap a
cap a 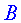 a través
del mirall i fa el triangle isòsceles). a través
del mirall i fa el triangle isòsceles).
és a dir, un total de 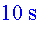 segons
segons
A la velocitat de la llum, cada costat val 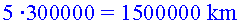
(aquest tren, ja ho hem dit, és molt gran)
En aquest temps, 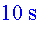 ,
i a la velocitat de ,
i a la velocitat de 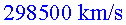 ,
(la velocitat de la nau de l’Ester), el tren ha recorregut ,
(la velocitat de la nau de l’Ester), el tren ha recorregut 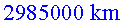
La llum a cada costat ha recorregut: 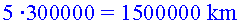
Com que és un triangle isòsceles, pel teorema de Pitàgores
podem calcular la distància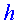 , ja que sabem la de la hipotenusa ,
, ja que sabem la de la hipotenusa , 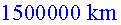 ,
i la del catet ,
i la del catet 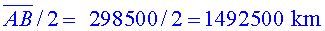 . .
Fets els càlculs, l’alçada tremenda del vagó del
tren és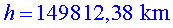 . .
b) El temps que l’Ester, a dalt del vagó, veurà
la llum viatjant.
La llum de l’Ester ha anat el línia recta
i ha recorregut el doble d’aquesta distància: 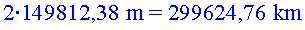 . .
El temps que ha tardat (segons l’Ester) el seu raig de llum ha estat el
següent, dividint la distància per la velocitat:
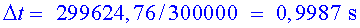 . Pràcticament . Pràcticament
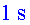 !. Una dècima
part igual que en el conte, en front dels !. Una dècima
part igual que en el conte, en front dels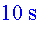 segons
que compta en Joan. segons
que compta en Joan.
c) L’Ester i en Joan no es posen d’acord amb la
trajectòria que segueix la llum. Qui té raó? Pel que fa
al temps que tarda la llum a fer el recorregut, també depèn de
l’observador. Es compleix la teoria de la relativitat?
Tenen raó tots dos, ja que el temps és
relatiu al sistema de referència. Tenint en compte la teoria d’Einstein,
la correcció relativista és aproximadament 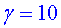 .
I està d’acord amb els temps que es mesuren des de fora i des de
dins del tren. .
I està d’acord amb els temps que es mesuren des de fora i des de
dins del tren.
La vida dels muons. Full de l’alumnat
Objectiu
 Comprendre la relativitat del temps. Comprendre la relativitat del temps.
 Veure’n un exemple real. Veure’n un exemple real.
Comprovació d’una realitat: el muó
| Els raigs còsmics
estan formats per moltes partícules que bombardegen la Terra i
que vénen de l’espai exterior. Sabem que els resultats d’aquests
bombardejos són partícules inestables que es destrueixen
molt ràpidament; però entre elles hi ha una partícula
que malgrat que és inestable, és la més estable de
totes: el muó.
I quèés el muó ?
El muó o partícula 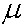 és una partícula de càrrega negativa igual que l’electró
però que té molta més massa. No es troba pas en l’àtom
però sí que surt com a subproducte de col·lisions,
tant naturals (raigs còsmics) com artificials (acceleradors, CERN
és una partícula de càrrega negativa igual que l’electró
però que té molta més massa. No es troba pas en l’àtom
però sí que surt com a subproducte de col·lisions,
tant naturals (raigs còsmics) com artificials (acceleradors, CERN ).
De totes les partícules creades en col·lisions és
la que té la vida mitjana més llarga: ).
De totes les partícules creades en col·lisions és
la que té la vida mitjana més llarga: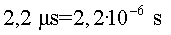 .
Quan el muó es desintegra dóna un electró, un neutrí
(muònic) i un antineutrí (electrònic). .
Quan el muó es desintegra dóna un electró, un neutrí
(muònic) i un antineutrí (electrònic).
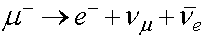
Totes les partícules es desintegren seguint una llei exponencial
negativa:
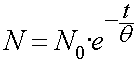
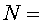 nombre de partícules que hi ha després del temps t
nombre de partícules que hi ha després del temps t
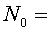 nombre de partícules
que hi havia en el temps zero nombre de partícules
que hi havia en el temps zero
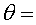 vida mitjana
de la partícula vida mitjana
de la partícula
La relació: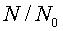 representa
el tant per u de partícules que encara “viuen” passat
el temps representa
el tant per u de partícules que encara “viuen” passat
el temps 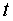 . Si
aquesta xifra la multipliquem per . Si
aquesta xifra la multipliquem per 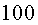 ,
tindrem el percentatge de partícules que encara no s’han
desintegrat en el temps ,
tindrem el percentatge de partícules que encara no s’han
desintegrat en el temps 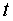 . .
Aquest percentatge valdrà:
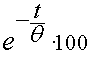
Calculem ara quin percentatge de muons arribaran a la
superfície de la Terra a partir d’aquesta equació.
Suposem que la velocitat dels muons és de 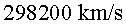 i que es formen per col·lisions dels raigs còsmics a
i que es formen per col·lisions dels raigs còsmics a 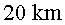 d’alçada
respecte del nivell del mar. El subproductes de totes les col·lisions
són muons i neutrins. Aquests últims, encara que siguin
estables, no es poden detectar per mitjans senzills. d’alçada
respecte del nivell del mar. El subproductes de totes les col·lisions
són muons i neutrins. Aquests últims, encara que siguin
estables, no es poden detectar per mitjans senzills.
|
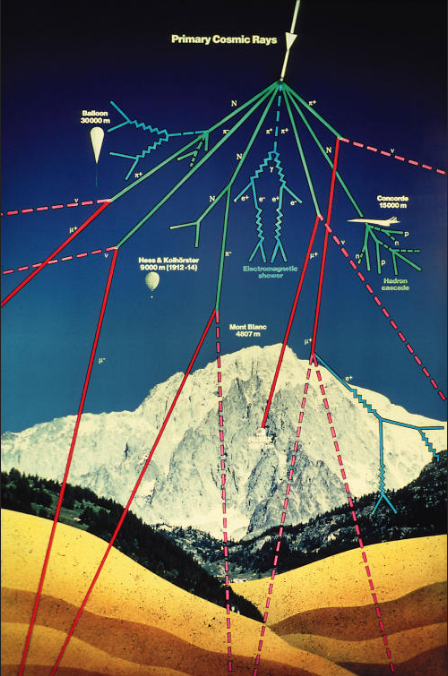 |
Fig. 5: El muó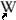 es una partícula de càrrega -1, i massa de 0,1056
GeV/c2. Forma part de la segona família de partícules
elementals conegudes com a Fermions. És un leptó, com l'electró,
però d'una generació i massa superiors.
es una partícula de càrrega -1, i massa de 0,1056
GeV/c2. Forma part de la segona família de partícules
elementals conegudes com a Fermions. És un leptó, com l'electró,
però d'una generació i massa superiors. |
Aplicant una senzilla equació del moviment uniforme (amb aquesta velocitat
inicial tan gran, considerar l'acceleració de la gravetat no altera significativament
el resultat), el temps que tardarien els muons des que es creen fins que arriben
al nivell del mar seria de:
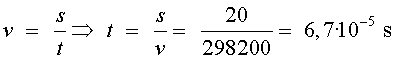
El percentatge de muons que arriben el nivell del mar serà doncs:
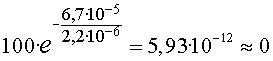
Per tant, no hi ha pràcticament cap muó que
arribi a la superfície de la Terra. Tots s’han desintegrat abans
d’arribar-hi.
Aquesta és la teoria. Però la realitat és molt diferent.
A l’inici de la dècada de 1940, dos científics americans,
B. Rossi i D.B. Hall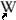 ,
a dalt d’una muntanya de ,
a dalt d’una muntanya de 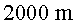 i
amb un detector de muons, van poder-ne detectar i
amb un detector de muons, van poder-ne detectar 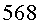 en una hora!
en una hora!
Si pensem en un muó que visqui exactament 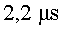 ,
la distància màxima que podrà recórrer, un cop format
a ,
la distància màxima que podrà recórrer, un cop format
a 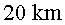 d’alçada,
és de: d’alçada,
és de:
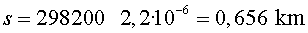
O sigui que, un cop recorreguts 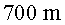 ni un sol muó estaria “viu”. Contràriament a la teoria,
a
ni un sol muó estaria “viu”. Contràriament a la teoria,
a 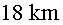 de l’origen
aquests científics en van detectar de l’origen
aquests científics en van detectar 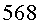 en una hora. És que viatgen més ràpid que la llum?
en una hora. És que viatgen més ràpid que la llum?
I l’experiència no acaba aquí. Els mateixos investigadors
van repetir l’experiment al nivell del mar.
Fent els càlculs teòrics, imaginant que hi ha 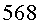 muons per hora a
muons per hora a 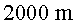 , quants
d’aquests arriben al nivell del mar? , quants
d’aquests arriben al nivell del mar?
El temps que tardarien a arribar-hi seria:
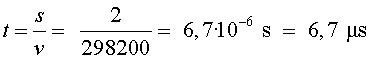
Calculem quants muons arribarien:
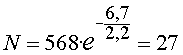
L’experiència es va fer i el detector va registrar l’arribada
de 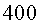 muons. Com es pot
explicar tot això? Si no podem sobrepassar la velocitat de la llum, vol
dir que els muons també han estat víctimes de la dilatació
del temps. muons. Com es pot
explicar tot això? Si no podem sobrepassar la velocitat de la llum, vol
dir que els muons també han estat víctimes de la dilatació
del temps.
Explicació
Explicació científica de l’arribada de muons amb vida
La velocitat de 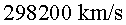 és igual a
és igual a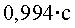 ( (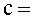 velocitat
de la llum en el buit, velocitat
de la llum en el buit, 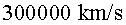 ).
La correcció relativista ).
La correcció relativista 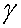 val:
val:
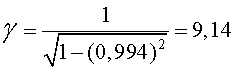
Per tant el temps que tardarien els muons a recórrer els 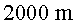 seria:
seria:
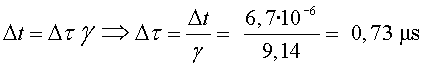
I, en aquest temps, el nombre de muons que arribaran al nivell
del mar serà:
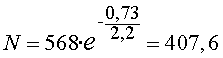
muons, d’acord amb l’experiment.
Abans hem calculat el percentatge de muons que arribarien al nivell del mar
un cop formats a 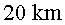 d’alçada
i vèiem que era zero. Calculem-ho ara tenint en compte la dilatació
del temps: d’alçada
i vèiem que era zero. Calculem-ho ara tenint en compte la dilatació
del temps:
El temps necessari per recórrer els 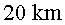 era de
era de 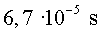 . .
Aplicant-hi la correcció relativista , aquest temps propi serà:
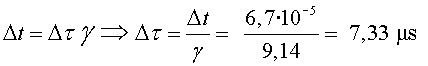
El percentatge de muons que arribarà serà ara
de:
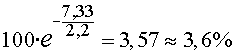
Un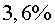 de muons ja és una quantitat apreciable.
de muons ja és una quantitat apreciable.
El mateix raonament l’haguéssim pogut fer modificant la vida mitjana
dels muons, multiplicant-la per 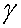 ,
que és exactament el mateix que dividir el temps nostre per ,
que és exactament el mateix que dividir el temps nostre per 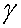 . .
Qüestionari
 Primera
qüestió: Primera
qüestió:
En totes les reflexions anteriors hem suposat que la velocitat dels
muons era de 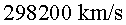 . Hem
de pensar que la velocitat que porten depèn de l’energia amb què
surten després de les col·lisions. Hi ha muons que viatgen a més
velocitat. Si imaginem que la velocitat dels muons és de . Hem
de pensar que la velocitat que porten depèn de l’energia amb què
surten després de les col·lisions. Hi ha muons que viatgen a més
velocitat. Si imaginem que la velocitat dels muons és de 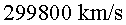 (que és encara més propera a la de la llum), quin percentatge
de muons arriben a la superfície de la Terra?
(que és encara més propera a la de la llum), quin percentatge
de muons arriben a la superfície de la Terra?
 Segona qüestió: Segona qüestió:
L’estratosfera on es produeixen les col·lisions dels raigs còsmics
és a 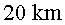 de la superfície
de la Terra. Per a un muó que viatja a de la superfície
de la Terra. Per a un muó que viatja a 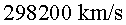 ,
aquesta distància sembla molt més curta. Per al muó, a
quina distància es troba l’estratosfera de la superfície
de la Terra? ,
aquesta distància sembla molt més curta. Per al muó, a
quina distància es troba l’estratosfera de la superfície
de la Terra?
La vida dels muons. Solucions
 En totes es reflexions
anteriors hem suposat que la velocitat dels muons era de En totes es reflexions
anteriors hem suposat que la velocitat dels muons era de 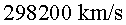 .
Hem de pensar que la velocitat que porten depèn de l’energia amb
què surten després de les col·lisions. Hi ha muons que
viatgen a més velocitat. Si imaginem que la velocitat dels muons és
de .
Hem de pensar que la velocitat que porten depèn de l’energia amb
què surten després de les col·lisions. Hi ha muons que
viatgen a més velocitat. Si imaginem que la velocitat dels muons és
de 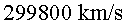 (que és
encara més propera a la de la llum), quin percentatge de muons arriben
a la superfície de la Terra? (que és
encara més propera a la de la llum), quin percentatge de muons arriben
a la superfície de la Terra?
La correcció relativista valdria:
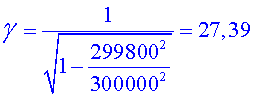
El temps que tardarien els muons que portessin aquesta velocitat seria de:
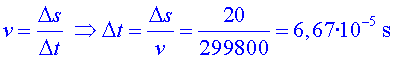
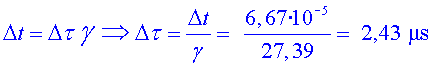
I el percentatge de muons que arribarien
a la superfície de la Terra seria de:
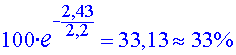
En aquest cas seria la quantitat apreciable
d’un  de muons
formats que arribarien a la Terra. de muons
formats que arribarien a la Terra.
 L’estratosfera on
es produeixen les col·lisions dels raigs còsmics és a L’estratosfera on
es produeixen les col·lisions dels raigs còsmics és a 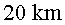 de
la superfície de la Terra. Per a un muó que viatja a de
la superfície de la Terra. Per a un muó que viatja a 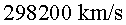 ,
aquesta distància sembla molt més curta. Per al muó, a
quina distància es troba l’estratosfera de la superfície
de la Terra? ,
aquesta distància sembla molt més curta. Per al muó, a
quina distància es troba l’estratosfera de la superfície
de la Terra?
El temps necessari per recórrer els 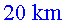 era de
era de 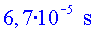 . Aplicant-hi
la correcció relativista, aquest temps propi serà: . Aplicant-hi
la correcció relativista, aquest temps propi serà:
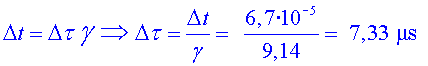
Per al muó, la distància 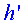 a
què es troba l’estratosfera de la superfície és a
què es troba l’estratosfera de la superfície és
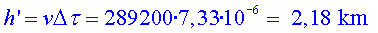
|

 5/10
5/10 