El moviment circular 
Material per als experiments
- Exp. A: suports, barres i pèndols.
- Exp. B: pots de vidre, pilotes de ping-pong, cordill,
cola de contacte.
- Exp. C: dinamòmetre, carret i pesos, cronòmetre,
càmera de fotos
Construcció de la plataforma
1. Marqueu els eixos de simetria a
la fullola.
2. Feu un forat de 20
mm al seu centre, per tal que hi pugui passar l'eix de la roda
3.Amb els tacs de fusta a les vores i les volanderes
al centre, adapteu la fullola a la llanta de bicicleta. Les volanderes
només serveixen per fer gruix; el nombre dependrà de com
siguin els tacs de fusta i la roda concreta que haguem comprat. Haurem
de posar les necessàries perquè la fullola s'adapti bé
i no balli.
4. Feu foradets als extrems de la fullola i lligueu-la
amb filferro a la roda de bici
5. Poseu el conjunt al suport, de manera que quedi
horitzontal.
6. Subjecteu el motoret amb una pinça i un suport,
a l'altura adequada
7. Enllaceu la roda de bici i el motor amb el cordó
elàstic.
8. Connecteu el motoret en sèrie amb el potenciòmetre
i la pila. La plataforma comença a girar: podeu regular-ne la
velocitat de gir amb el potenciòmetre |
|
Experiments
A. L'acceleració centrípeta augmenta amb la distància
al centre
Ho podem veure de dues maneres:
a) Posem damunt la plataforma dos suports i una barra
horitzontal. D'aquesta barra hi pengem quatre pèndols: un just
damunt de l'eix i els altres cada vegada més allunyats de l'eix.
Quan la roda gira, els pèndols se separen de la vertical. L'angle
que formen amb la vertical és més gran com més
gran és la distància a l'eix.
|
|
| Un possible treball de continuació
seria relacionar angles amb distàncies a l'eix i velocitat angular.
Els angles es poden mesurar sobre la foto i les distàncies també,
si es disposa de l'escala adequada.
b) Posem quatre discs de fusta alineats, a distàncies
creixents de l'eix de gir. Quan la roda comença a girar, qui
subministra la força centrípeta als discs és la
fricció. La velocitat angular creix i la fricció arriba
al límit. Els discs comencen a escapar-se tangencialment, per
ordre de distància a l'eix.
També es pot veure que a la imatge els discs surten més
moguts més gran és la distància a l'eix
(la velocitat lineal és proporcional al radi).
|
|
B. L'acceleració centrípeta
va cap al centre
Es tracta de posar damunt la plataforma dos pots invertits (lligueu-los
entre si amb un cordill!) amb pilotes de ping-pong a dins. Quan la plataforma
gira, les pilotes de ping-pong assenyalen la direcció i sentit
de l'acceleració.
(vegeu l'article de Tavi Casellas "Una nou
contra Newton", publicat en aquesta revista la primavera
de 2009)
(vegeu també l'article de V. Grau "Un
senzill acceleròmetre que desafia el sentit comú",
en aquest mateix número de la revista) |
|
C. Mesurem la força centrípeta
Posem un dinamòmetre horitzontalment damunt la plataforma i hi lliguem
un carret de poca fricció, de manera que el carret quedi a uns 15
cm o 20 cm
de l'eix.
Prèviament, haurem d'haver enganxat una escala de distàncies
a la fullola.
Fem girar la plataforma i deixem estabilitzar la velocitat de gir.
Fem fotografies del dinamòmetre i del carret.
Cronometrem el temps que tarda a donar 10
voltes. Amb això trobarem el període T
de rotació. A la foto del carret hi podrem veure la distància
a l'eix R.
Amb aquestes dades podem calcular la força centrípeta  .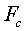
A la vegada el dinamòmetre fa una mesura directa del valor de la força
centrípeta, que l’expressarem amb
. Podem comparar aquest dos valors.
Aquestes són dues mesures:
|
Exp. n. 2:
m
= 300 g ; R
= 24 cm; t(10
voltes) =
10,82 s ;  .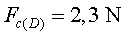
Amb aquestes mesures obtenim: T
= 1,08 s;  ; ;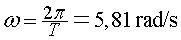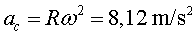
 .
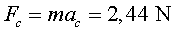Novament, la força mesurada amb el dinamòmetre (2,3
N) i la calculada (2,44
N) són prou semblants.
|
|
Així doncs, veiem que els resultats surten prou coherents: la discrepància
relativa entre el valor esperat de la força centrípeta i el que
assenyala el dinamòmetre és, en els dos casos, inferior al 10%.
|
8/10 
.
.
de
(El podeu
adquirir a la botiga Onda-radio, al carrer Gran Via, 581,
de Barcelona, o a qualsevol altra botiga d'electrònica).
.
; 
; 
.
