núm 0 Mostra |
Tardor del 2007 |
Societat Catalana de Física |
| Inici |
| Sumari |     2/7  |
 | El Pèndol Elàstic Emilio Llorente |
| És freqüent que en les activitats experimentals es produeixin fenòmens que semblen no ajustar-se a les previsions teòriques. Sovint, quan pengem un cos d’una molla per estudiar el MHS, en separar el cos de la posició d’equilibri i deixar que oscil·li lliurement, al cap d’unes poques oscil·lacions comença a fer coses “rares”. El moviment sembla que es desestabilitza: el cos va cap els costats i es posa a oscil·lar com un pèndol.. Parem el moviment i tornem a separar el cos de l’equilibri amb més cura, però torna a fer el mateix, sembla un moviment caòtic que no podem controlar. Si això passés a l’alumne estaríen dient-li que la molla no està ben subjectada, o que ja d’entrada el desplaçament de l’equilibri està mal realittzat... Si ho fa l’alumne pensaríem “està clar que no ho fa bé”, però i si ens passa als professors? |
Aquest cas s'anomena pèndol elàstic: el cos penjat d’una molla pot oscil·lar tant verticalment, MHS, com amb un moviment pendular, i passa d’un a l’altra en determinades condicions de ressonància. Això succeeix quan el període de vibració és la meitat que el període d’oscil·lació pendular, és a dir, mentre el cos vagi d’un costat a l’altre haurà de pujar i baixar. En aquestes tres fotografies s’observa que quan el cos passa pel centre en el moviment d’oscil·lació, està en el punt més alt del moviment vibratori vertical, i quan passa pels extrems, es troba en els punts més baixos.
A la pàgina d'en Peter Lynch, The Swinging Spring System (http://www.maths.tcd.ie/~plynch/SwingingSpring/SS_Home_Page.html),
s’expliciten les equacions diferencials del moviment i també hi
ha diverses simulacions.
i com que els períodes són
ens quedarà:
i en l’equilibri, la llei de Hooke ens dóna la relació
Ens quedarà
que, en reduir-la, Aquesta seria, en una primera aproximació, el valor
de la massa que hauríem de penjar per què la molla passes espontàniament
d’un mode de vibració a l’altre. L’energia passa d’estar
en l' MHS al pendular i així successivament. També es pot observar
que el pla d’oscil·lació del pèndol cada vegada és
diferent.
En penjar dues molles en sèrie es pot donar el cas que la massa de la segona molla sigui just la necessària perquè la primera entri en ressonància: per tant no serà necessari penjar una massa. A l’adreça : http://www.baldiri.org/fq/treballs_recerca/ es poden trobar tres vídeos, gravats per Nesrim, en els quals s’observen aquests fenòmens.
|
,
,
.
.
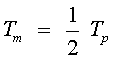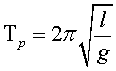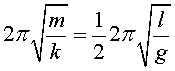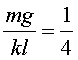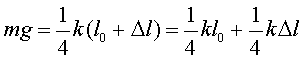
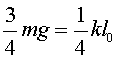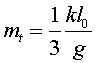s'hauria
de tenir en compte la massa de la molla (o la seva fracció efectiva,
que segons determinats autors és 
de
la seva massa quan es fa la determinació dinàmica del període
i 
en la llei de Hooke).
La longitud 
és
la de la molla, però, com que oscil·la, també hi pot influir
la longitud afegida del suport de les masses. Si considerem negligibles aquests
valors, i tenint en compte que 
( 
és la longitud
de la molla sense cap massa), la condició d'acoblament quedaria:
.
,
.
de cada
ressort. Després penjava masses de valor semblant al que donava la condició
de ressonància i observava si es produïa el fenomen. Va estudiar
també la variació del pla d’oscil·lació pendular.
respecte
d l'últim pla.
