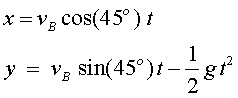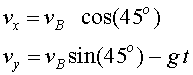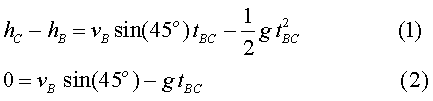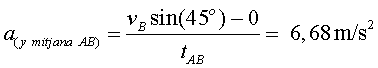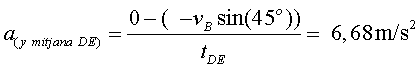núm 1 |
Primavera del 2008 |
Societat Catalana de Física |
| Inici |
| Sumari |     9/9 |
 | Problemes d'aquí i d'allà Salvador Estradé |
| L’objectiu d’aquesta secció és proposar i resoldre problemes que siguin estimulants i atractius per a l’alumnat (i per a nosaltres) i que en fomentin l'interès per la física. Voldríem que el professorat s’animés a col·laborar-hi i que ens enviés les seves propostes a sestrade@xtec.cat i engresqués el seu alumnat a participar-hi. En cada número hi haurà una proposta i se'n publicarà la millor solució o la més original. |
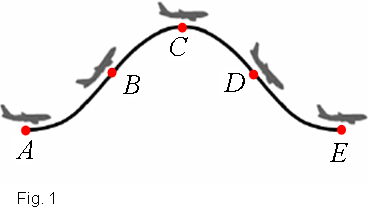
Començarem amb un problema de nivell de batxillerat que es va proposar a la fase espanyola de l’Olimpíada de Física de l’any 2007. Es tracta d'un problema relacionat amb la creació artificial de condicions de microgravetat. Aquestes condicions s'utilitzen tant per a la recerca cientifica com per a l'art! ( vegeu a la la Revista de física 4 (3) pàg. 55 l'escrit "Ballar sense gravetat o la insuportable lleugeresa de l'ésser" de Josep Perelló). Enunciat  La campanya anual de vols parabòlics que promou des de fa anys l’Agència Espacial Europea (ESA) permet que més d’un centenar d’estudiants universitaris realitzin experiències dissenyades per ells mateixos en condicions de gravetat aparent nul·la a bord d’un avió Airbus A300. La descripció d’aquest tipus de vol, representat esquemàticament en la figura 1, és la següent: l’avió arriba al punt A volant horitzontalment a la seva velocitat màxima. Després s’eleva i quan aconsegueix una altura de 25000 ft sobre el nivell del mar amb un angle de 45º (punt B), redueix la potència dels motors fins al mínim necessari per contrarestar la pèrdua d’energia produïda per la fricció amb l’aire. En aquesta primera fase del vol (tram AB), que dura 20 s, els passatgers noten que el seu pes aparent quasi es duplica.
Aquesta maniobra es repeteix unes 30 vegades en cada vol, que té una durada total d’unes dues hores i permet realitzar experiències en condicions d’ingravidesa (microgravetat) durant el tram BCD. a) Escriviu les equacions de la posició
i la velocitat de l’avió en el tram parabòlic. Notes: Per a més informació sobre aquests vols: http://www.esa.int/education/parabolic
 SolucióLa nostra solució és:
a) Les equacions que determinen el moviment de l’avió
en el tram parabòlic (BCD)
si agafem com a origen de les coordenades el punt B
són: on, d'acord amb l'enunciat, Per a la velocitat:
Aïllant el temps de (2), substituint-lo a (1) i fent les operacions corresponents,
n’obtenim:
Si un observador que es troba situat a l’exterior de l’avió, en un sistema inercial (un observador fix sobre la superfície terrestre es pot considerar un bon observador inercial per a aquest cas), aplica la llei fonamental de la dinàmica a un passatger de massa m, n’obté segons l’eix vertical:
on
Així doncs, la gravetat aparent que notarà el passatger dins de l’avió en el tram AB és1,68 g. En el tram DE del vol, l’avió baixa i frena. Per tant, la component vertical de la velocitat és negativa i la de l’acceleració positiva. La mitjana de la component vertical de l’acceleració en aquest tram es pot calcular igual que abans, a partir del canvi experimentat per la component vertical de la velocitat de l’avió en passar de D a E (cal tenir en compte que l’avió a D, perquè conserva l’energia mecànica, porta la mateixa velocitat que tenia a B i, a més, la simetria de la trajectòria parabòlica comporta que arribi a D amb una inclinació descendent de 45º). Així doncs:
Justament el mateix resultat que en el tram AB.
El valor de Així doncs, la gravetat aparent dins de l’avió
en el tram DE
també és
|
|||||||||||||||||
.
i que la
component vertical de 
és
nul·la. Així doncs, tenim:
; i el valor de
s’ha
calculat directament de (2). 
és
la component vertical de la força mitjana que l’avió (concretament
el seient de l’avió) exerceix sobre el passatger. El seu valor
és:
.
i, en conseqüència, la gravetat aparent que nota un passatger a
l’interior de l’aparell és nul·la.
