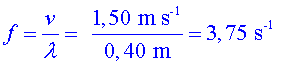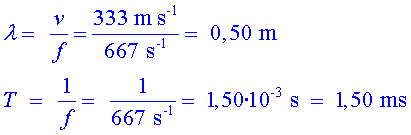Ones i soEncara que el so i les ones siguin essencialment el mateix que eren fa 50 anys, les possibilitats tecnològiques fan que avui sigui assequible per als alumnes de secundària accedir a l'anàlisi d'aquests fenòmens d'una manera molt diferent. Ara és fàcil analitzar sons reals o moviments vibratoris harmònics simples (MVHS) reals i no limitar-se a les equacions.
A partir de cada un dels paràgrafs dels continguts del currículum (textos dins dels requadres), se’n proposen problemes relacionats.  
Full de l'alumnat
| Les ones i el
so 1: Realització d'experiències de
captura i enregistrament de sons generats per objectes vibrants amb micròfons.
Caracterització de les magnituds associades: període, freqüència,
fase, amplitud, característiques sinoidals. Estudi experimental
de la posició, velocitat, acceleració d'un moviment harmònic
simple (MHS). Interpretació de les transformacions energètiques
en un MHS.
|
| 1.
S'ha enregistrat la posició d'un objecte de 200
g unit a una molla horitzontal. L'objecte, inicialment en repòs
es va empènyer cap a l'esquerra i posteriorment es va deixar
anar iniciant, aproximadament, un moviment harmònic simple.
a) Determina l'amplitud inicial del
moviment i el seu període.
b) Calcula l'energia mecànica
en els moments inicials (quan encara no havia disminuït l'amplitud).
c) Calcula la força amb queè
es va empènyer l'objecte inicialment.
|

|
| Fig. 1 |
| Les ones i el
so 2: Caracterització de les ones sonores:
model basat en la vibració d'un objecte i la transmissió
de la pertorbació per l'aire fins a arribar a les nostres oïdes.
Reconeixement de la transferència d'energia sense transferència
de matèria com a característica general de les ones. Utilització
de models mecànics i simulacions per ajudar a la comprensió
del model. Realització de càlculs sobre la velocitat de
propagació d'una ona.
|
| 2.
Es mostren dos fotogrames separats per 0,064
s de la filmació d'una cubeta d'aigua en la què un
vibrador (situat a l'esquerra) produïa unes ones. La filmació
s'ha fet a 250
fotogrames per segon i s'hi ha superposat un objecte de 5
cm per tenir la indicació de l'escala. Considera que entre
les dues imatges ha transcorregut menys d'un període.
a) Determina la longitud d'ona, la velocitat de propagació
i la freqüència de l'ona.
b) Quina diferència de fase
hi ha entre les dues imatges?
|

|
| Fig. 2: origen de la imatge: Department of Physics. Doane College. Crete,
NE (USA) |
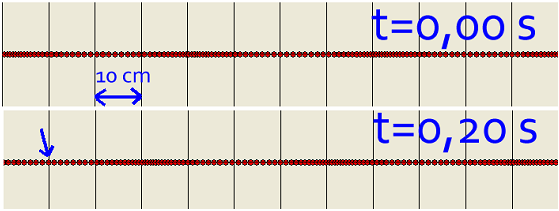
| 3.
Les imatges mostren dues captures de la simulació d'una ona en
un medi unidimensional representat per un seguit de boletes unides entre
si. La pertorbació es propagava cap a la dreta. La segona imatge
es posterior és 200
ms a la primera i les línies verticals estan separades 10
cm entre si.
a) Determina la longitud d'ona, la velocitat de propagació
i la freqüència de l'ona simulada.
b) Indica on serà la partícula
assenyalada amb una fletxa en la segona imatge quan hagi passat un període.
c) Indica justificadament la naturalesa
de l'ona aquí simulada: (mecànica / electromagnètica,
longitudinal / transversal).
|
|
| Fig. 3: |
| Les ones i el
so 3: Identificació de diferents tipus d'ones:
mecàniques (en diferents medis) i electromagnètiques. Diferenciació
d'ones longitudinals i transversals. Caracterització de les magnituds
d'una ona periòdica: amplitud, període, velocitat de propagació,
freqüència, longitud d'ona i fase. Interpretació de
la doble periodicitat espai-temps.
|
| 4.
Un altaveu que vibra amb una freqüència de 667
Hz produeix una ona sonora plana que es desplaça per l'aire
a 333 m/s.
L'ona produeix una pertorbació de 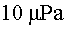 d'amplitud. d'amplitud.
a) L'altaveu provoca una pertorbació que es propaga:
a quina magnitud física correspon aquesta pertorbació i,
per tant, en quines unitats l’hem de mesurar?
|
|
| Fig. 4: |
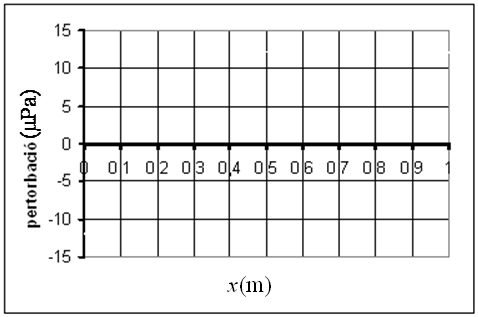
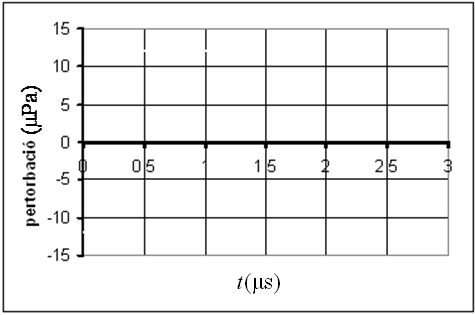
| b) Dibuixa
els gràfics pertorbació-temps i pertorbació-posició
( vegeu les figures 4 i 5). Considera que en el moment inicial i en 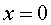 la
pertorbació era de la
pertorbació era de 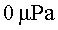 i
augmentava. i
augmentava.
|
|
| Fig. 5: |
| Les ones i el
so 4: Comprensió i aplicació del principi
de Huygens. Reflexió i refracció. Interferències:
constructives i destructives. Observació experimental i interpretació
dels fenòmens de reflexió, refracció, interferències
i difracció. Reconeixement de l'efecte Doppler i les seves aplicacions.
|
| 5.
La figura 6 mostra els fronts d'ones planes que arriben a una superfície
plana amb un angle d'incidència de 45º
i s'hi reflecteixen.
Fes una figura similar per a cada una de les situacions
següents. Explica en cada cas quina o quines de les magnituds de
l'ona canviaran (i com) després del fenomen produït i el nom
del fenomen.
a) Una front d'ones sonores que viatgen per l'aire (v
= 340 m/s) arriben amb un angle d'incidència de 15º
a un medi en el qual la velocitat del so és de 680
m/s.
b) Un feix d'ones sonores planes de
230 Hz de freqüència
arriba a una paret amb un orifici de 50
cm d'ample.
c) Una sirena que emet un so de 1000
Hz s'allunya de nosaltres a 34
m/s .
d) Ens arriba el so que prové
de 2 altaveus que produeixen, en fase i amb la mateixa intensitat, un
so de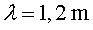 i que estan
situats a una distància de 3,6
m i 5,4 m
de nosaltres, respectivament. i que estan
situats a una distància de 3,6
m i 5,4 m
de nosaltres, respectivament.
|

|
| Fig. 6: reflexió d'ones planes. |
| Les ones i el
so 5: Caracterització del so: intensitat,
to i timbre. Interpretació de gràfics de sons captats per
mètodes informàtics o electrònics i determinació
de les magnituds rellevants.
|
| 6.
La figura 7 mostra el registre de la veu d'una persona que pronuncia una
e oberta. L'escala de temps està indicada en segons.
|
 |
| Fig. 7 |
a) a. Determina el període
i la longitud d’ona del so fonamental d'aquesta veu (velocitat del
so en l’aire: v
= 340 m/s).
|
| Les ones i el
so 6: Observació d'ones estacionàries
en instruments musicals de corda i vent. Interpretació de la producció
d'una ona estacionària. Aplicació del principi de superposició.
Reconeixement de sons fonamentals i harmònics. Observació
de la representació d'un so pur i d'un so complex. Construcció
d'un so complex a partir de sons purs. Identificació de sons purs
en sons complexos.
|
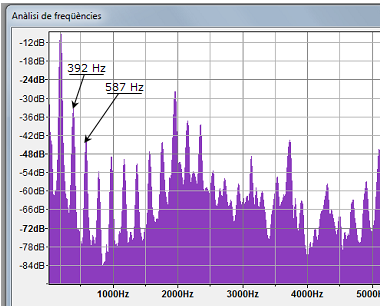
| 7.
La figura 8 mostra l'espectre de freqüències d'un so complex
(arxiu sonor en format MP3 so_i.mp3). S'han indicat
les freqüències del segon pic (392
Hz) i del tercer pic (587
Hz).
a) Identifica quins pics corresponen al so fonamental
i quins als sobretons. Calcula la freqüència del so fonamental
i la del vuitè harmònic i identifica'ls al gràfic.
b) Quin és el sobretò
més important?
|
|
| Fig. 8:: espectre de freqüències d'un so. |
| Les ones i el
so 7: Reconeixement de l'escala de l'oïda humana.
Aplicació dels ultrasons. Diferència entre so i soroll.
Mesura del soroll. Contaminació acústica.
|
| 8.
La figura 9 mostra tres registres sonors.
|
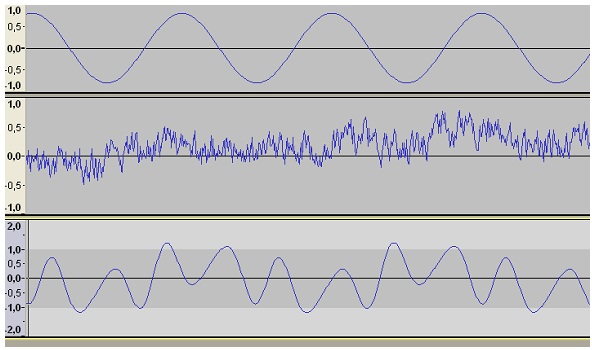 |
| Fig. 9 |
a) Indica quin dels tres
registres correspon a un soroll, quin a un so complex i quin a un so pur.
Justifica la resposta comparant les freqüències de cada cas. |
| 9.
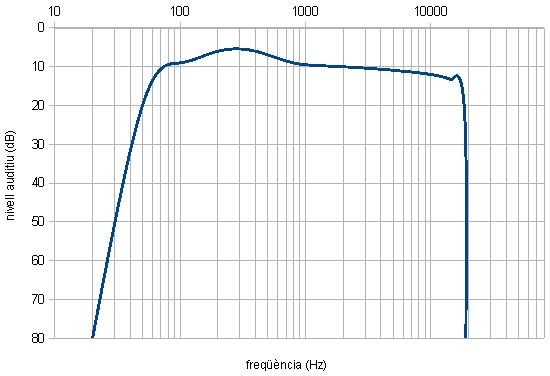
La figura 10 mostra un audiograma d'una persona jove amb audició
normal. A les ordenades s'indica, per a cada freqüència, la
intensitat mínima necessària per poder percebre els sons.
a) La major part de les persones perden progressivament
la capacitat de sentir els sons aguts. Dibuixa com podria ser l'audiograma
d'una persona de mitjana edat.
b) A l'article "Hearing range"
de la Wikipedia  http://en.wikipedia.org/wiki/Hearing_range hi hem trobat aquest text:
http://en.wikipedia.org/wiki/Hearing_range hi hem trobat aquest text:
Dogs
The hearing ability of a dog is dependent on its breed and age. However,
the range of hearing is approximately 40
Hz to 60000
Hz, [6] which is much greater than that of humans. As with humans,
some dog breeds become more deaf with age, [...]"
Com seria l'audiograma d'un gos?
|
|
| Fig. 10: audiograma d'una persona jove amb audició
normal. |
c) Imagina que la persona de l'audiograma
de la figura està sentint un soroll que té una freqüència
al voltant dels 1000 Hz
amb un nivell de sensació sonora de 70
dB. En quin factor s'haurà de reduir la intensitat sonora perquè
deixi de sentir-lo?
d) Imagina que la persona de l'audiograma de la figura sent
un soroll que ve del carrer que té una freqüència al voltant
dels 1000 Hz i amb
un nivell de sensació sonora de 60
dB. Si s'instal·la a les parets de casa un aïllament acústic
que absorbeix el 99,99%
de l'energia sonora, seguirà sentint el soroll?
Nota: les qüestions c i d
es proposen com a alternatives.

 
Solucions
1. S'ha enregistrat
la posició d'un objecte de 200
g unit a una molla horitzontal. L'objecte, inicialment en repòs
es va empènyer cap a l'esquerra i posteriorment es va deixar anar iniciant,
aproximadament, un moviment harmònic simple.
a) Determina l'amplitud inicial del moviment
i el seu període.
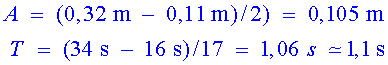
b) Calcula l'energia mecànica en els
moments inicials (quan encara no havia disminuït l'amplitud).
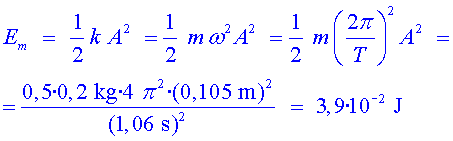
c) Calcula la força amb que es va
empènyer l'objecte inicialment.

2. Es mostren dos fotogrames
separats per 0,064 s
de la filmació d'una cubeta d'aigua en la que un vibrador (situat a l'esquerra)
produïa unes ones. La filmació s'ha fet a 250
fotogrames per segon i s'ha superposat un objecte de 5
cm per a tenir indicació de l'escala. Considera que entre les
2 imatges ha transcorregut menys d'un període.
a) Determina la longitud d'ona, la velocitat de propagació
i la freqüència de l'ona.
8 longituds d'ona ocupen 6
cm* a la imatge ( cm*
són els mesurats pel nostre regle sobre la imatge) . Considerant un factor
d'escala 5 cm = 1,75 cm*
tenim que 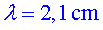 . .
També es veu que el front d'ona ha avançat 0,5
cm* entre les 2 imatges (correspon a 1,43
cm) d'on
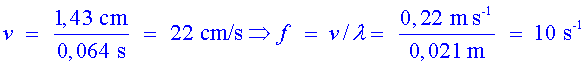
b) Quina diferència de fase hi ha
entre les dues imatges?
Com s'han avançat 1,43
cm i la  , , 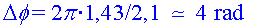 (o
bé, a partir del període, (o
bé, a partir del període, 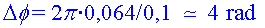 ) )
3. Les imatges mostren
dues captures de la simulació d'una ona en un medi unidimensional representat
per un seguit de boletes unides entre si. La pertorbació s'estava propagant
cap a la dreta. La segona imatge es posterior a la primera en 200
ms i les línies verticals estan separades 10
cm entre si.
a) Determina la longitud d'ona, la velocitat de propagació
i la freqüència de l'ona simulada.
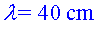 ; ;
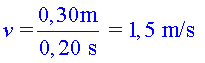 ; ; 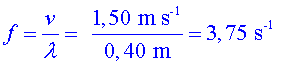
b) Indica on es trobarà la partícula
assenyalada amb una fletxa en la segona imatge quan hagi passat un període.
Al mateix lloc on està ara.
c) Indica justificadament la naturalesa de
l'ona aquí simulada (mecànica / electromagnètica) , (longitudinal
/ transversal) . mecànica, ja que les boletes que oscil•len són
partícules materials. Longitudinal, ja que el moviment de les boletes
coincideix en direcció amb el desplaçament de la pertorbació.
Mecànica, ja que les boletes que oscil•len
són partícules materials. Longitudinal, ja que el moviment de
les boletes coincideix en direcció amb el desplaçament de la pertorbació.
| 4.
Un altaveu que vibra amb una freqüència de 667
Hz produeix una ona sonora plana que es desplaça per l'aire
a 333 m/s.
L'ona produeix una pertorbació de 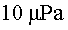 d'amplitud. d'amplitud.
a) L'altaveu provoca una pertorbació que es propaga,
a quina magnitud física correspon aquesta pertorbació i,
per tant, en quines unitats la mesurem?
El so correspon a variacions de pressió de
l'aire per això la mesurem en  (micropascals). (micropascals).
|
|
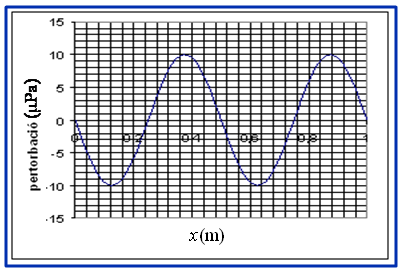
| Fig. 11a: |
| b) Dibuixa
els gràfics pertorbació-temps i pertorbació-posició
( vegeu figures 4 i 5). Considera que en el moment inicial i en 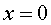 la
pertorbació era de la
pertorbació era de 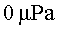 i
estava creixent. i
estava creixent.
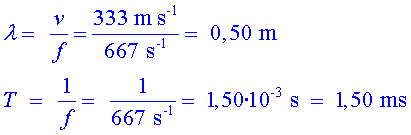
amb aquestes dades construim les
corresponents gràfiques que es poden veure a les figures 11a i
11b.
|

|
| Fig. 11b: |
| 5.
La figura 6 mostra els fronts d'ones planes que arriben a una superfície
plana amb un angle d'incidència de 45º
i s'hi reflecteixen.
Fes una figura similar per a cada una de les següents situacions.
Explica en cada cas quina o quines de les magnituds de l'ona canviaran
(i com) després del fenomen produït i el nom del fenomen.
a) Una front d'ones sonores que viatgen per l'aire (v
= 340 m/s) arriben amb un angle d'incidència de 15º
a un medi en el que la velocitat del so és de 680
m/s.
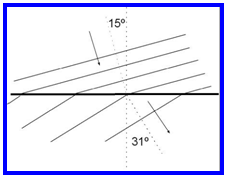
Refracció: Canviarà
la longitud d'ona(es duplicarà) i la direcció de propagació
(es separarà de la normal, des de 15º fins a 31º). Vegeu
la figura 12.
b) Un feix d'ones sonores planes de
230 Hz de freqüència
arriba a una paret amb un orifici de 50
cm d'ample.
Difracció: Canvia la forma
dels fronts d'ona que passen de plans a gairebé esfèrics
(pot dir-se que canvia la direcció).Vegeu la figura 13.
c) Una sirena que emet un so de 1000
Hz s'allunya de nosaltres a 34
m/s .
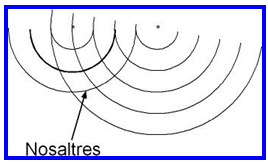
Efecte Doppler: A la zona on estem
nosaltres augmenta la longitud d'ona i disminueix la freqüència.
Vegeu la figura 14.
d) Ens arriba el so que prové
de 2 altaveus que produeixen, en fase i amb la mateixa intensitat, un
so de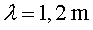 i que estan
situats a una distància de 3,6
m i 5,4 m
de nosaltres, respectivament. i que estan
situats a una distància de 3,6
m i 5,4 m
de nosaltres, respectivament.
Interferència destructiva:
L'amplitud disminuirà i serà la diferència de les
amplituds de les ones que arriben. (Encara que les amplituds siguin iguals
als altaveus, l'amplitud de l'ona que prové de l'altaveu més
pròxim serà major que la de l'altre). Vegeu
la figura 15. |
|
| Fig. 12: reflexió d'ones planes |
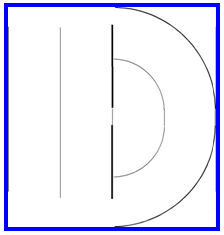 |
| Fig. 13: difracció d'ones planes |
 |
|
 |
|
| Fig. 13: efecte Doppler. |
|
Fig. 15: Interferència |
|
| Les ones i el
so 5: Caracterització del so: intensitat,
to i timbre. Interpretació de gràfics de sons captats per
mètodes informàtics o electrònics i determinació
de les magnituds rellevants.
|
| 6.
La figura 7 mostra el registre de la veu d'una persona pronunciant una
e oberta. L'escala de temps està indicada en segons.
|
a) a. Determina el període
i la longitud d’ona del so fonamental d'aquesta veu. (velocitat
del so en l’aire: v
= 340 m/s).
El patró 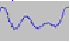 es repeteix 11
vegades entre 1,400
s i 1,475
s, per tant
es repeteix 11
vegades entre 1,400
s i 1,475
s, per tant

Nota: Un alumne espavilat podria fer notar que es veu
clarament la presència del tercer harmònic, de període
un terç del període fonamental.
|
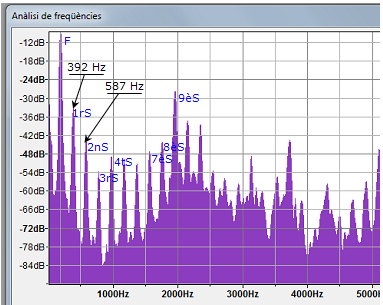
| 7.
La figura 8 mostra l'espectre de freqüències d'un so complex
(arxiu sonor en format MP3 so_i.mp3). S'han indicat
les freqüències del segon pic (392
Hz) i del tercer pic (587
Hz).
a) Identifica quins pics corresponen al so fonamental
i quins als sobretons. Calcula la freqüència del so fonamental
i la del vuitè harmònic i identifica'ls al gràfic.
El so fonamental correspon al primer
pic i els altres als sobretons. Vegeu la figura 16.
Es veu molt clarament que hi ha pics per a cada múltiple enter
de la freqüència fonamental, que deu ser 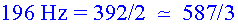
.
Nota: En l'espectre real el programa donava com a freqüència
del primer pic 199
Hz). El vuitè harmònic deu correspondre a  (realment
el pic està a 1.561
Hz) i està assenyalat a la figura com a setè sobretò
(7èS). (realment
el pic està a 1.561
Hz) i està assenyalat a la figura com a setè sobretò
(7èS).
b) Quin és el sobretò
més important?
El pic amb més intensitat, després
del fonamental, és el del 10è
harmònic o 9è
sobretò, en teoria a 1.960
Hz (realment a 1.951
Hz).
|
|
| Fig. 16:: espectre de freqüències
d'un so. |
Més
informació: El so pot escoltar-se al fitxer adjunt ( so_i.mp3)
i conté una veu d'home pronunciant el so "i". El so va
ser analitzat amb el programa  ,
un fragment del fitxer de so pot veure’s a la figura 17 on es pot
veure com hi ha 23,5
períodes entre 1,38
s i 1,50 s (f = 195,8 Hz). ,
un fragment del fitxer de so pot veure’s a la figura 17 on es pot
veure com hi ha 23,5
períodes entre 1,38
s i 1,50 s (f = 195,8 Hz). |
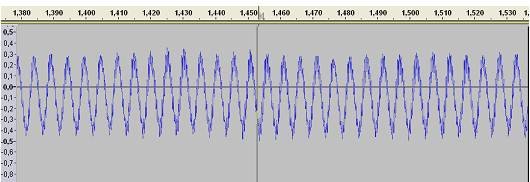 |
| Fig. 17:: espectre de freqüències
d'un so. |
| 8.
La figura 9 mostra 3 registres sonors.
|
a) Indica quin d'ells
correspon a un soroll, quin a un so complex i quin a un so pur. Justifica
la resposta comparant les freqüències presents en cada cas. |
El primer correspon a un so pur:
s’aprecia una ona harmònica amb una única freqüència,
el segon a un soroll: s'aprecia una funció aparentment aleatòria,
sense cap patró discernible i el tercer a un so complex, ja que
s'aprecia periodicitat, però no és una ona harmònica
simple ja que hi ha vàries freqüències - amb relació
simple- superposades.
|
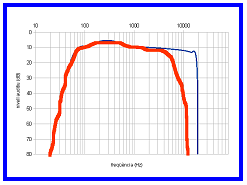
| 9.
La figura 10 mostra un audiograma d'una persona jove amb audició
normal. En ordenades s'indica, per a cada freqüència, la intensitat
mínima necessària per a poder percebre els sons.
a) La major part de les persones perden progressivament
la capacitat de sentir els sons aguts. Dibuixa com podria ser l'audiograma
d'una persona de mitjana edat.
La gràfica de la figura
18pot ser-ne un exemple.
|
|
| Fig. 18: |
| b) A l'article
"Hearing range" de la Wikipedia  http://en.wikipedia.org/wiki/Hearing_range hem trobat aquest text:
http://en.wikipedia.org/wiki/Hearing_range hem trobat aquest text:
"...Dogs
The hearing ability of a dog is dependent on its breed and age. However,
the range of hearing is approximately 40
Hz to 60000
Hz,[6] which is much greater than that of humans. As with humans,
some dog breeds become more deaf with age,[7] ... "
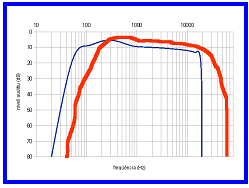
Com seria l'audiograma d'un gos? Vegeu la figura 19.
|
|
| Fig. 19: |
c) Imagina que la persona de l'audiograma
de la figura està sentint un soroll de freqüència al voltant
dels 1000 Hz amb
un nivell de sensació sonora de 70
dB. En quin factor s'haurà de reduir la intensitat sonora per
tal de que deixi de sentir-lo?
Com el seu llindar auditiu a 1000
Hz està a 10
dB, caldria que la sensació sonora es reduís en 60
dB = 6 B, es a dir que la intensitat sonora disminuís fins a un
valor 10-6
vegades l'original.
d) Imagina que la persona de l'audiograma de la figura està
sentint un soroll que ve del carrer de freqüència al voltant dels
1000 Hz i amb un
nivell de sensació sonora de 60
dB. Si s'instal·la a les parets de casa un aïllament acústic
que absorbeix el 99,99%
de l'energia sonora, seguirà sentint el soroll?
L'aïllament del 99,99%
deixarà passar un 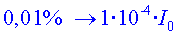 i
com i
com
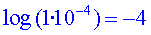 , l'aïllament
reduirà la sensació sonora en 4
B = 40 dB, de manera que la persona dins de casa sentirà el soroll
a 20 dB, com està
per sobre del seu llindar d'audició a aquesta freqüència,
sí podria sentir el soroll, encara que, la veritat, no crec que li pugui
molestar gaire. , l'aïllament
reduirà la sensació sonora en 4
B = 40 dB, de manera que la persona dins de casa sentirà el soroll
a 20 dB, com està
per sobre del seu llindar d'audició a aquesta freqüència,
sí podria sentir el soroll, encara que, la veritat, no crec que li pugui
molestar gaire.
Nota: les qüestions c
i d es proposen com alternatives.

|

 5/9
5/9 














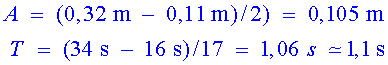
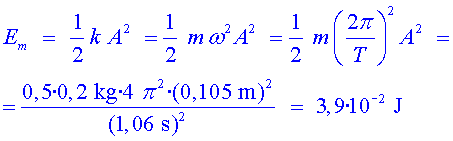

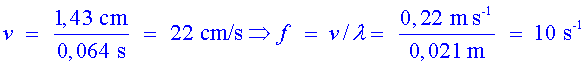
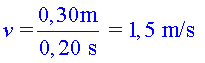 ;
;