núm 10 |
Tardor del 2012 |
Societat Catalana de Física |
| Inici |
| Sumari |     9/9 |
 | El racó obscur Xavier Jaén |
| L’electromagnetisme ha estat sempre envoltat d’un aire misteriós. Aquest misteri ha estat, sense voler-ho, reforçat amb l’elecció de les unitats emprades en els càlculs. No és nou culpar de l’embolic de les unitats les dificultats que hom troba en explicar l’electromagnetisme. Però tampoc no és nou la manca de propostes encaminades a desfer aquest embolic. El caldo de cultiu és doncs propici per posar-hi cullerada. |
Ampere, on vas?
IntroduccióEn les disciplines cientificotècniques no només
volem tenir una explicació "satisfactòria" del món
que ens envolta; volem que aquesta explicació sigui contrastable (per
a molts això vol dir verificable, a alguns ens agrada dir, en la línia
de Karl Poppe, , Per acord internacional, tots els observadors defineixen els patrons d’espai i temps de la mateixa manera. La BIPM (Oficina Internacional de Pesos i Mesures) és l’organisme que supervisa l’SI (sistema internacional d’unitats). Poden canviar d'aquí no gaire, però actualment les definicions són: Unitat de temps. El segon, s: un interval temporal d'1 segon és igual a 9192631770 períodes de la radiació corresponent a la transició entre els dos nivells hiperfins dels estats fonamentals de l’àtom de cesi 133. (adoptada el 1967) Unitat de distància. El metre, m: un interval espacial d'1 metre és igual a la distància recorreguda per la llum en el buit durant un interval de temps de 1/299792458 segon. ( adoptada el 1983) A més, cal afegir-hi la definició de massa (gravitatòria? inercial?) per completar el que s'anomena MKS ( massa, kilogram, segon), que és el germen de l’SI. Per entendre’ns, l'MKS seria l'extracte de l’SI que fa referència a la mecànica. Tradicionalment amb l'MKS podem fer mecànica, però no electromagnetisme. Això ja és un primer fet estrany si tenim en compte que la mecànica és el metallenguatge per tractar el moviment (espai i temps) i les seves causes (forces o interaccions). Podem tractar la força gravitatòria, la d'una molla, les forces de fricció... però no les d'origen electromagnètic. Com si aquestes fossin "especials". Però de fet tots sabem, i expliquem, que a nivell microscòpic la força que genera una molla, o la fricció, tenen l’origen en forces electromagnètiques. És més, als alumnes els diem que hi ha dues forces fonamentals a la natura: la gravitatòria, tan dèbil que només es fa notar quan un dels cossos és enorme, i l'electromagnètica, que governa quasi tot el que ens envolta... I resulta que no és mecànica? Aquest racó obscur pretén remenar una mica aquestes qüestions. Està basat essencialment en dos treballs. El primer [1] fa un resum del problema des del punt de vista estrictament de les unitats i tenint-ne present la repercussió en l'àmbit professional i educatiu sense entrar en aspectes conceptuals. El segon [2] és un treball recent en què l'objectiu no era tractar problemes d'unitats, però en el qual precisament una "bona" elecció de les unitats electromagnètiques permet entendre més fàcilment la teoria de la gravitació de Newton.
|
falsable |
(1) |
Si un cos de massa gravitatòria Mg interactua amb un altre de massa inercial m i gravitatòria mg tenim, segons la llei de gravitació de Newton combinada amb (1):
 |
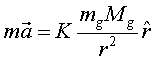(2) |
El que va observar Newton, i d'altres, és que l'acceleració
de tots els cossos que interaccionen amb
Mg és la mateixa. Això vol dir que
el quocient 
és
una constant universal que pot ser absorbida per l'altra constant universal,
K. Així,
va fer 
i escriure
 |
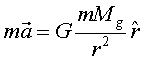(3) |
i va anomenar G
la constant de gravitació universal, tal com
la coneixem actualment. La igualtat
és entre dos conceptes diferents. Només si utilitzem les mateixes
unitats podem expressar que són iguals. Abans de decidir que cal
mesurar els dos conceptes amb les mateixes unitats. La qüestió important
aquí és que si 
,
aquest fet no seria motiu suficient per prohibir fer servir les mateixes unitats
per als dos conceptes.
Les unitats electromagnètiques
L'embolic d'unitats que podia haver sorgit a la gravitació
no va arribar a més per dos motius: el primer perquè el fet que
"l'acceleració de tots els cossos que interacionen amb
Mg és la mateixa" invita a escollir
i, el segon, perquè en la gravitació de Newton no hi ha "efectes
magnètics". En l'electromagnetisme no tenim cap dels dos motius.
És per això que, històricament, ha sorgit un considerable
embolic d'unitats que ha contribuït a deixar l'electromagnetisme fora de
la mecànica i se li ha donat aquest aire misteriós que encara
avui llueix. Vegem-ho amb més detall. Usualment la interacció
electromagnètica es descriu a través de:
1) La força de Lorentz: la trajectòria
d'una partícula de càrrega
i massa (inercial)
en el si d'un camp electromagnètic
, sempre que la partícula es mogui amb velocitat petites respecte de la velocitat de la llum, és la solució de l'equació de moviment:
 |
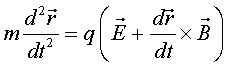(4) |
2) Les equacions de Maxwell: el camp electromagnètic
 |
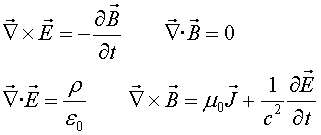(5) |
on
és la densitat de càrrega i
la densitat de corrent presents.
A més tenim la relació entre constants:
 |
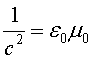(6) |
Tal com hem fet amb la gravitació, a l'expressió
(2) i tal com es fa als articles [1-4], afegirem
les necessàries constants a (4) i (5)
que ens permetin la llibertat d'elecció d'unitats. Hom veu que es poden
escriure les equacions de Lorentz-Maxwell introduint 4 constants
en la forma
 |
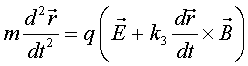(7) |
 |
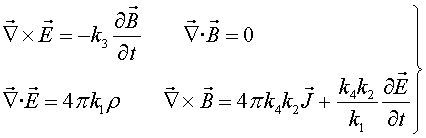(8) |
Les constants
es poden escollir lliurement sempre que compleixin
 |
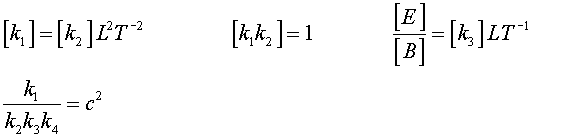(9) |
Les diferentes eleccions de les constants estan lligades als diferents sistemes d'unitats. A llarg del temps se n'han proposat alguns que aquí recordem:
Per començar, notem que en tots els casos apareix la constant c, no sempre al numerador.
L' MKS-racionalitzat utilitza com unitats el metre, el kilogram i el segon i afegeix l'ampere. La definició actual que dóna la BIPM de l'ampere és:
Unitat de corrent elèctrica :l'ampere és el corrent constant que, en dos conductors paral·lels rectilinis de longitud infinita, de secció circular negligible, separats un metre en el buit, causaria entre aquests dos conductors una força igual a 2 × 10-7 newtons per metre de longitud.
Resulta sorprenent que l'ampere es defineix en termes de newtons, metres... és a dir en termes de metre-kilogram-segon. L'"ampere internacional" original fou definit electroquímicament com el corrent necessari per dipositar plata a un ritme d'1,118 mg/s d'una solució de nitrat de plata. La definició històrica de l'ampere el tractava, aparentment, com una unitat bàsica. Sigui com sigui, actualment sabem que no és una unitat bàsica, però es continua tractant com si ho fos per raons pràctiques i/o històriques [1].
Només el primer (UES) és un sistema d'unitats
coherent, en el sentit que permet fer el límit 
.
Si volem tractar l'electromagnetisme i fer referència a efectes relativistes,
etc, necessitem que el sistema d'unitats no amagui aquestes cartes sota la màniga.
Nosaltres, tal com fem a [2], en proposem un de nou que, a
més de ser coherent, està adaptat especialment a la comparació
entre interaccions. El podem anomenar MKS-pur:
on 
és
la constant de gravitació universal. Si redefinisim la unitat kg
de manera que 
, llavors
l'MKS-pur passa a ser l'UES. Però si volem mantenir una unitat de massa
associada a un objecte, com per exemple el bloc de París, tal com es
fa a la teoria de la gravitació, és convenient mantenir el valor
de usual.
Unitat de massa : el kilogram, kg, una massa d'1 kilogram és igual a la massa (inercial) del patró internacional: un cilindre d’iridi-platí custodiat a París per la BIPM. (adoptat el 1889)
Així tindrem que un objecte no té dos, sinó tres tipus de massa: la massa inercial, la massa gravitatòria i la massa electromagnètica (o, si es vol, la podem anomenar càrrega elèctrica, però la mesurarem en kilograms).
En l'MKS-pur les equacions de Maxwell-Lorentz s’escriuen:
 |
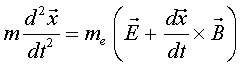(10) |
 |
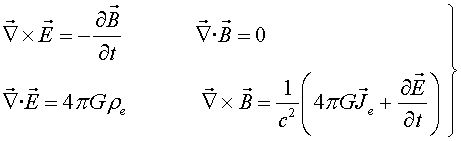(11) |
Hem canviat el símbol de
càrrega pel més adient 
que
emfatitza el fet que en aquest sistema d’unitats les masses ( inercial
o gravitatòries) i les càrregues es mesuren en les mateixes unitats.
Pot semblar que el que hem fet es "només jugar amb les unitats" i que això no té significat físic, que hom pot treballar amb les unitats que vulgui. Això no és cert del tot. No tots els sistemes d'unitats són coherents. L'elecció del sistema d'unitats no és en absolut independent de la teoria. Vegem-ne algun exemple en relació amb l'electromagnetisme.
Amb aquest primer pas (equacions (10) i (11))
el que hem fet és aproximar electromagnetisme i gravitació. Podem
aproximar-los més si fem el límit no relativista de (10)
i (11). Bé, de fet (10) ja és
essencialment no relativista, però no (11). Si
fem, estrictament, i
fem servir les condicions usuals a l'infinit (nul·litat dels camps) les
equacions (10) i (11), esdevenen
 |
(12) |
 |
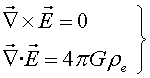(13) |
ja que les equacions per al camp magnètic són
i
tenen la solució 
,
que és compatible amb les condicions a l'infinit. Un fet notable és
que en aquestes unitats coherents es veu clar que el camp magnètic
és un efecte totalment relativista!
Així encara s'apropen més electromagnetisme i gravitació. Les equacions per la interacció gravitatòria (no relativista) són:
 |
(12) |
 |
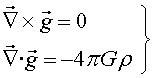(13) |
Notem que les úniques diferències formals entre les equacions electromagnètiques i gravitatòries no relativistes són :
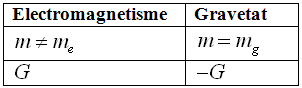
Ara, qui s'atreveix a dubtar que l'electromagnetisme no és mecànica?
Finalment, les lleis de la gravitació de Newton i de Coulomb en l’MKS-pur es poden expressar de la manera següent:
 |
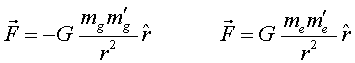(14) |
Reflexions finals
Hem vist que l'elecció d'unes unitats o unes altres
no és una qüestió purament de conveniència. Des del
punt de vista estrictament conceptual, l'elecció de les unitats està
estretament lligada al desenvolupament de la mateixa teoria. No podem deslligar
un fet de l'altre. La mateixa teoria que desenvolupem ha de preveure com mesurem.
Ja ens agradaria poder ser objectius i definir a priori les unitats i els sistemes
de mesura i després desenvolupar i jutjar quina teoria és "la
bona".
Vol dir això que les unitats que ensenyem als alumnes són incorrectes?
No, de cap manera. Però el que sí que cal que reconeguem és
que no són fruit d'un desenvolupament lògic de la teoria, sinó
més aviat d'un procés històric no tan senzill d'entendre
(per a nosaltres i per als alumnes) i molt difícil de treure’s
de sobre per raons fonamentalment pràctiques. No només ensenyem
física per saber com funciona el món. Normalment ens veiem empesos
a capacitar els alumnes en la modificació de la realitat que els envolta
sense que els calgui una comprensió tan profunda d'aquesta. Si és
difícil, per als organismes internacionals, la modificació de
les unitats electromagnètiques és perquè hi ha moltíssims
professionals que en el seu dia a dia fan servir les unitats actuals i, probablement,
només en traurien que maldecaps si les haguessin de canviar. Així
que, tranquils, de moment tenim ampere per a anys.
Bibliografía
[1] Guissard, A. Electrical Units and Electromagnetic Field Vectors IEEE Transactions on Education Vol. E-15, N. 1, February 1972
[2] Jaén, X., Molina, A. Rigid motions and generalized Newtonian gravitation. Lost in Translation . arXiv:1210.1137 [gr-qc]
[3] Jackson, J.D. Classical Electrodinamics. John Wiley p. 825 (1975).
[4] Llosa, J. i Molina, A.Relativitat especial amb aplicacions a l'electrodinàmica clàssica. Edicions UB, 81, p.206 (2005)
