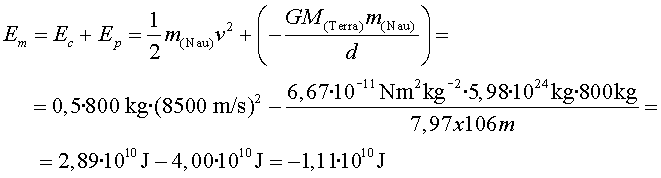núm 11 |
Primavera del 2013 |
Societat Catalana de Física |
| Inici |
| Sumari |   5/9 5/9  |
| Problemes empaquetats Octavi Plana |
|
| Com als problemes empaquetats anteriors, els problemes proposats estan agrupats a partir dels paràgrafs del currículum de física de batxillerat. En aquest número abordem el segon tema: planetes i satèl·lits. |
Planetes i satèl·litsIntroduccióQui no ha deixat volar la imaginació amb fabuloses naus espacials de ciència-ficció en exòtics sistemes planetaris? L'exploració de l'espai ens proporciona actualment molts exemples fascinants sobre l'aplicació dels continguts relacionats amb el camp gravitatori en situacions reals.
Avui dia hi ha tantes dades disponibles de missions espacials reals i d'observacions astronòmiques, i és tan fàcil aconseguir-les, que seria una llàstima haver de proposar als alumnes problemes referits a situacions que no existeixen. Al mateix temps, possiblement les situacions reals excitaran molt més la curiositat de l'alumnat i evitarem problemes artificiosos. D'acord amb l'abundància i diversitat de fonts disponibles, s'ha intentat que les dades apareguin en els enunciats amb diferents formats: mapes celestes, fotogrames, pàgines web oficials de missions. De la mateixa manera també es demanen les respostes en diferents formats: a més de les típiques resolucions per càlcul numèric es demana la construcció de gràfics, la redacció d'explicacions, el càlcul d'errors i la representació gràfica de vectors.
|
|
1. La figura
1 mostra la posició aparent del cometa C/2009
P1, principalment visible durant l'any 2011, respecte al firmament
tal com es veu des de la Terra. Proposa una explicació per a
la forma de tirabuixó de l'òrbita aparent. |
|
|
| Fig. 1 |
| Planetes i satèl·lits
2: Comprensió
i aplicació de la gravitació universal. Càlcul
de la força gravitatòria sobre un cos a la superfície
i a diferents altures sobre la Terra i d'altres astres. Relació
d'identitat entre la força gravitatòria i la força
centrípeta en les òrbites (suposadament circulars) dels
planetes i dels satèl•lits. Aplicació al càlcul
de paràmetres orbitals per a òrbites circulars: períodes,
velocitats i radis. |
2. La ISS vola a una
òrbita aproximadament circular a uns![]() d'altura
sobre la superfície de la Terra. Dins seu hi ha 2 astronautes amb una
massa
d'altura
sobre la superfície de la Terra. Dins seu hi ha 2 astronautes amb una
massa ![]() .
.
a) Amb quina força atreu la Terra cada un dels dos astronautes?
Compara-la amb el pes dels astronautes quan eren a la superfície de la
Terra.
b) Com és que “floten” dins la nau?
c) Calcula la velocitat i l'acceleració (des de la Terra)
de cada un dels dos astronautes.
La ISS perd altura lentament a causa de la la fricció amb l'atmosfera
(uns ![]() cada mes) i cada
cert temps els motors de la nau l'han de tornar a pujar.
cada mes) i cada
cert temps els motors de la nau l'han de tornar a pujar.
d) Indica com anirà variant la massa, el pes real i
el pes aparent d'un astronauta a la ISS mentre la nau va perdent altura.
Dades: ![]() ,
,
![]() ,
, ![]()
| Planetes i satèl·lits
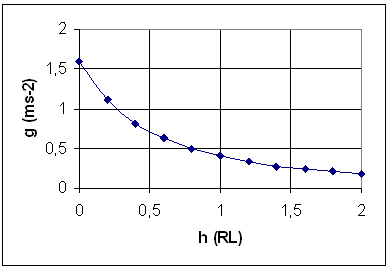
3: Reconeixement i interpretació
de la intensitat del camp gravitatori: relació entre la intensitat
del camp gravitatori i l'acceleració de la caiguda lliure. Coneixement
de la variació de |
| 3.
La intensitat del camp gravitatori a la superfície de la Lluna
és de |
|
| Fig. 2: |
|
|
|
| Fig. 3: |
| Planetes i satèl·lits
4: Comprensió i aplicació
de l'energia potencial gravitatòria. Determinació de l'energia
necessària per enviar un satèl•lit a una òrbita
circular o per enviar-lo fora del camp gravitatori de la Terra. Velocitat
d'escapament. |
| 5.
La nau Dawn va ser llançada amb la missió d'explorar dos
asteroides: Vesta i Ceres. Considera que en el moment de màxima
proximitat a Vesta estava en una òrbita circular a
|
|
| Fig. 4: font imatge: http://ca.wikipedia.org/wiki/Fitxer:Dawn-image-070911.jpg |
| Planetes i satèl·lits
5: Caracterització de
naus espacials i satèl•lits artificials. Aplicació
en camps diversos. Recerca d'informació de dades de les naus,
dels seus llançaments i de detalls orbitals. Estudi, mitjançant
simulacions, de diferents paràmetres orbitals d'una nau espacial.
Anàlisi de diferents tipus d'òrbites en funció
de l'energia mecànica. |
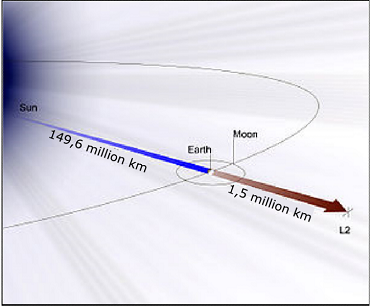
| 6.
El telescopi espacial Webb es llançarà el 2014 o el 2015
i girarà en una òrbita circular al voltant del Sol al
punt L2. Aquest punt està alineat amb el Sol i la Terra, a a) Calcula la força gravitatòria total
que actuarà sobre el telescopi Webb, de Dades:
|
|
| Fig. 5: font imatge:adaptat de http://en.wikipedia.org/wiki/File:L2_rendering.jpg |
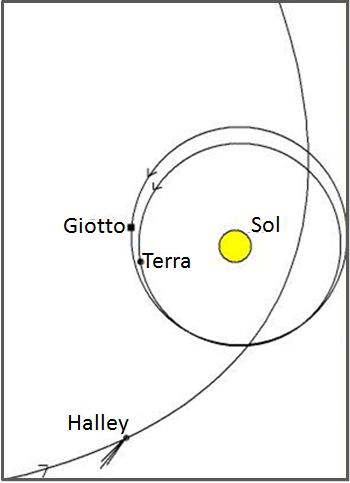
| 7. La missió Giotto va consistir a enviar una nau espacial perquè es trobés amb el cometa Halley. La figura (no està a escala) mostra les trajectòries de la Terra, del cometa Halley i de la nau Giotto poc mesos abans de la trobada. a) En el moment de màxima proximitat la nau
va passar a
|
|
| Fig. 6: font imatge:simplificada a partir de http://en.wikipedia.org/wiki/File:Giotto_Halley_e_Grigg-Skjellerup.png |
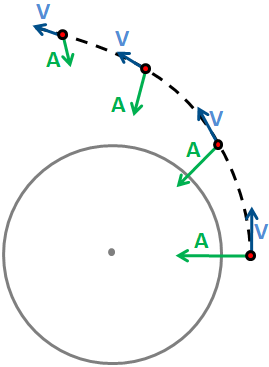
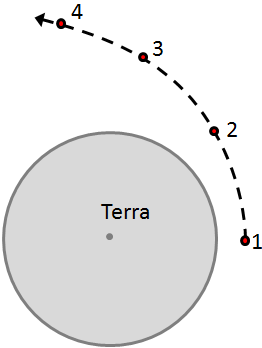
| 8.
La figura mostra la Terra i una nau espacial de a) Dibuixa, sobre cada un dels 4 punts vermells representant la nau (vegeu la figura 7), el vector acceleració, A, i el vector velocitat,V de manera que quedi ben clara quina és la direcció i el sentit i en quins casos són més grans o més petits aquests vectors. b) Les velocitats i les distàncies de la nau al centre de la Terra es recullen en aquesta taula
Determina l'energia mecànica de la nau. Tornarà a passar
la nau pel punt 1 o es troba en una òrbita oberta? Justifica
la resposta. |
|
||||||||||||||||||||
| Fig. 7 |
9. XMM-Newton és
el satèl·lit més gran llançat per l'Agència
Espacial Europea. La seva massa és de ![]() (
(![]() és
el simbol de tona). A la pàgina web de la missió (http://sci.esa.int/science-e/www/object/index.cfm?fobjectid=31349)
hem trobat la següent informació sobre la seva òrbita.
és
el simbol de tona). A la pàgina web de la missió (http://sci.esa.int/science-e/www/object/index.cfm?fobjectid=31349)
hem trobat la següent informació sobre la seva òrbita.
Orbit/NavigationOrbit insertionXMM-Newton reached its operational orbit less than a week after being launched by Ariane 5. The satellite was initially injected into a temporary orbit, with a perigee of 850 km and an apogee of 114 000 km, and then utilised its own propulsion system to raise the perigee. Forty minutes after the satellite
was released from the launcher upper stage, telemetry from XMM-Newton
confirmed that the solar arrays had deployed. After checking the satellite's
health and its correct orientation, engineers at the Mission Control
Centre waited almost one day (22 hours) until XMM-Newton reached its
first apogee. At that precise moment they ordered the first of four
(eventually five) firings of XMM-Newton's thrusters, four (plus another
four for redundancy) small jets using hydrazine propellant. Each boost
occurred at apogee, progressively raising the perigee to 7000 km. |
|
| Fig. 8:ESOC Main control room from which the XMM-Newton early orbit phase was controlled. |
Meanwhile the telescope
tube was emptied of any residual gases (outgassing), the sunshield deployed,
and finally the doors of the mirror modules opened. Operational orbitXMM-Newton's operational orbit
is highly eccentric (reaching nearly one third of the distance to the
Moon) and has been chosen for two reasons. First the XMM-Newton instruments
need to work outside the radiation belts surrounding the Earth. These
radiation belts are filled with highly energetic particles and extend
out to about 40 000 km from the Earth. The radiation of the accelerated
particles can cause both damage to the science instruments and false
readings. |
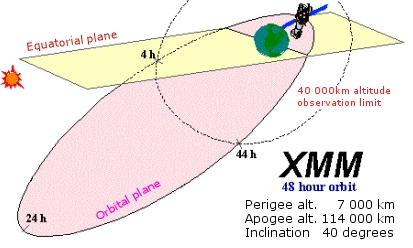 |
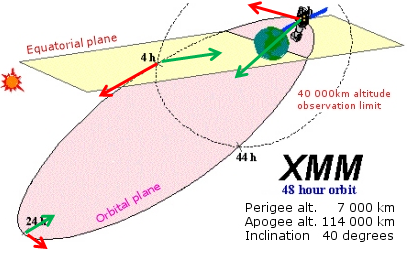
| Fig. 9:Schematic of XMM-Newton's operational orbit at the start of the mission |
Com pots comprovar, distingeixen entre l'òrbita a la
qual el va deixar el coet llançador, “òrbita d'inserció”,
i l’“òrbita operacional”, en la qual el satèl•lit
estava en les condicions òptimes de funcionament.
a) Compara les dues òrbites: En
quina té més energia mecànica? En quina té un període
més gran? Quins elements orbitals són iguals en les dues òrbites?
b) Quant de temps passa a cada òrbita
a menys de ![]() d'altura
? I a més de
d'altura
? I a més de ![]() ? A què es deu aquesta diferència tan gran?
? A què es deu aquesta diferència tan gran?
c) Dibuixa sobre la figura el vector
velocitat i el vector acceleració al perigeu, a l'apogeu i al punt marcat
“![]() ”.
”.
d) En quin punt de l'òrbita es
van posar en marxa els motors per passar de l'òrbita d'inserció
a l'òrbita operativa? Com hauria estat l'òrbita resultant si s'haguessin
posat en marxa els motors just a l'extrem contrari de l'òrbita?
e) A quin punt convindria frenar el satèl•lit
al final de la seva vida operativa si volem que s'acabi desintegrant a l'atmosfera
terrestre?
Solucions
Planetes i satèl·lits 1.1.
La clau és la "posició aparent". Veiem el cometa des de la Terra, que no constitueix un sistema de referència inercial. Les voltes del tirabuixó corresponen al moviment del la Terra al voltant del Sol (una volta cada any). Aquests girs estan combinats amb el moviment del cometa, que cal tenir present que és més aparent quan està més a prop de la Terra, tant per l'efecte de proximitat com perquè coincideix amb els moments de màxima velocitat (periheli).
Planetes i satèl·lits 2.2.
a)
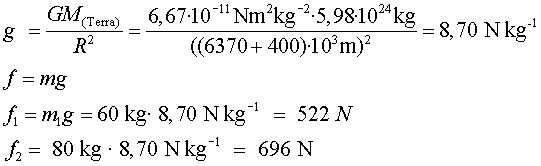
Aquestes forces són menors que a la superfícies
de la Terra, ja que ![]() és
més petita. Podem comparar-les quantitativament i dir que seran
és
més petita. Podem comparar-les quantitativament i dir que seran
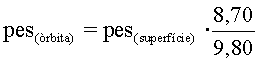 o bé
o bé 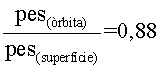
b) Pot argumentar-se que la nau és un sistema de referència
no inercial amb una acceleració centrípeta, a causa de la seva
òrbita circular de ![]() ;
de manera que per a un observador a la nau els astronautes tenen una acceleració
aparent
;
de manera que per a un observador a la nau els astronautes tenen una acceleració
aparent![]() .
.
c) L'acceleració és igual a la ![]() ,
ja que els astronautes estan en caiguda lliure (mentre no hi actuï a sobre
cap força diferent del pes); així doncs,
,
ja que els astronautes estan en caiguda lliure (mentre no hi actuï a sobre
cap força diferent del pes); així doncs, ![]() (apuntant cap al centre de la Terra).
(apuntant cap al centre de la Terra).
Podem trobar ![]() a partir
de
a partir
de 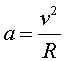 , ja que estan en
una òrbita circular i l'única acceleració és l'acceleració
centrípeta:
, ja que estan en
una òrbita circular i l'única acceleració és l'acceleració
centrípeta:
![]()
(òbviament en la direcció tangent a l'òrbita i en el sentit de l'avanç)
d) La massa no variarà (en tot cas no variarà
per aquest motiu).
El pes real augmentarà quan disminueixi l'altura , ja que ![]() augmentarà, encara que cal dir que el canvi serà molt petit: en
un mes
augmentarà, encara que cal dir que el canvi serà molt petit: en
un mes ![]() passarà
de
passarà
de ![]() a
a ![]() , de manera que
, de manera que 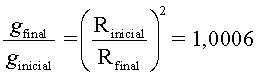 , és
a dir un augment del
, és
a dir un augment del ![]() .
.
El pes aparent no canviarà, ja que serà nul en tot moment.
Observacions: pot remarcar-se aquí que les respostes quantitatives són
millors que les qualitatives (per exemple, en les 2 comparacions que es demanen).
| Planetes i satèl·lits 3.3. Serà suficient marcar 3 punts
|
|
| Fig. 10: |
Planetes i satèl·lits 3.4.
a) Cal mesurar a la foto (vegeu la figura
3) l'altura de l'astronauta,![]() ,
i la del salt,
,
i la del salt,![]() , i fer
una proporció. A mi m'ha donat :
, i fer
una proporció. A mi m'ha donat : ![]() ;
per tant, el salt deu ser de
;
per tant, el salt deu ser de 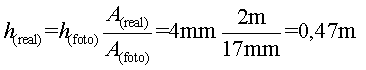 .
.
Per a una caiguda lliure sense velocitat inicial 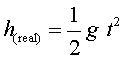 , per tant,
, per tant, 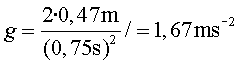 .
.
b) Per a un punt situat a la superfície d' una massa
esfèrica, 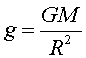 ,
, 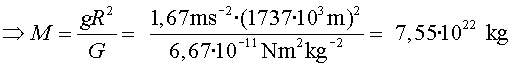
c) Els errors absoluts seran ![]()
![]()
i ![]()
i els errors relatius 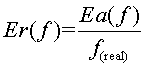
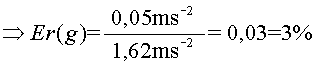 i
i 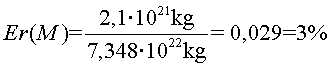
En aquest exercici és evident que no a tothom li donarà exactament
igual (llevat que s'ho copiïn), ja que depèn de mesures bastant
poc precises. El resultat presentat és sorprenentment exacte si considerem
les estimacions de les dades inicials.
Planetes i satèl·lits 4.5.
Es troba en una òrbita circular al voltant de Vesta
de radi ![]()
a) 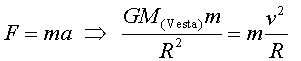
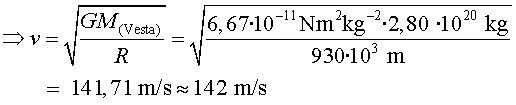
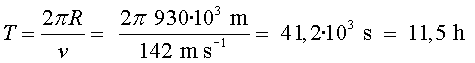
b) Perquè quedi en una òrbita lliure, cal que
com a mínim l'energia sigui zero. Calculem primer l'energia que tenia
en l'òrbita circular:
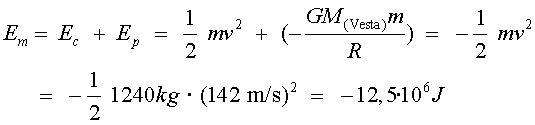
Per tant caldrà subministrar, com a mínim, ![]() perquè
pugui escapar de l'atracció de Vesta.
perquè
pugui escapar de l'atracció de Vesta.
Planetes i satèl·lits 5.6.
a) Quan el telescopi estigui al punt L2 experimentarà
l'atracció de la Terra, amb una força
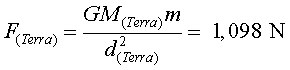
i l'atracció del Sol, amb una força
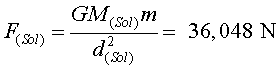
Com que les dues forces són tenen la mateixa direcció i sentit,
la força total tindrà el mòdul
![]()
b) 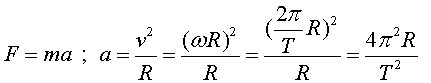 ,
,
per tant
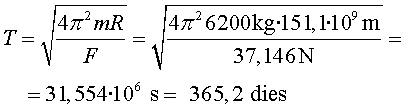
És remarcable que una nau en el punt L2 dóna
voltes al voltant del Sol amb el mateix període que la Terra, encara
que està a més distància de la nostra estrella. Aquest
fet és un dels requisits de disseny del telescopi, tal com diu l'enunciat.
El que hem fet aquí es comprovar que es compleix.
Planetes i satèl·lits 5.7.
a) Poden calcular-se els mòduls de ![]() i
i ![]()
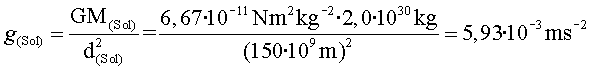
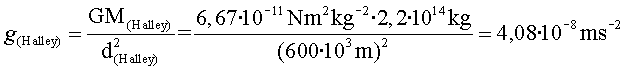
de manera que![]() és
molt més gran, de l'ordre de
és
molt més gran, de l'ordre de ![]() vegades
vegades ![]() .
.
Podria arribar-se a una comparació vàlida calculant simplement
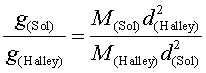
La conclusió és que la trajectòria de la nau pràcticament
no serà afectada per la proximitat al cometa.
b) El període de Giotto és de![]() .
Se'n pot trobar el semieix major aplicant la 3a llei de Kepler, atès
que tant la Terra com Giotto orbiten al voltant del Sol:
.
Se'n pot trobar el semieix major aplicant la 3a llei de Kepler, atès
que tant la Terra com Giotto orbiten al voltant del Sol:
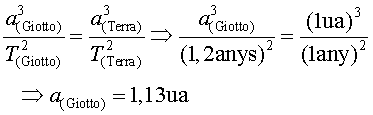
| Planetes i satèl·lits 5.8. a) Cal que quedi clar que el vector A apunta cap al centre de la Terra, i no cap al centre de l'òrbita ni en direcció perpendicular a V (llevat del punt 1) o paral·lela a l'òrbita. Cal també que es mostri que el mòdul va disminuint. El vector velocitat V ha de ser sempre tangent a l'òrbita i decreixent. b) Qualsevol de les files de la taula és suficient
per a calcular l'energia mecànica. |
|
| Fig. 11: |
| Planetes i satèl·lits 5.9. a) Ambdues òrbites tenen el
mateix apogeu i comparteixen el pla orbital, però l'òrbita
operativa té un perigeu més allunyat; per tant, el seu
semieix major és més gran i també serà més
gran el seu període. b) Està c) Vegeu la figura 12. Les velocitats estan etiquetades en vermell i les acceleracions en verd. d) Els motors es posen en marxa en passar per l'apogeu.
e) Convindria frenar-lo, per exemple amb retrocoets,
en passar per l'apogeu; així disminuiria l'altura del perigeu
fins a caure a l'atmosfera. |
|
| Fig. 12: |




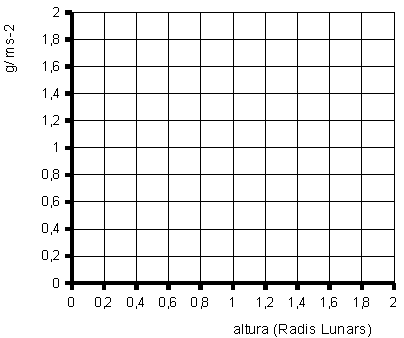



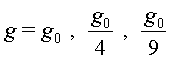 , i notar que la línia ha de tendir a zero quan
, i notar que la línia ha de tendir a zero quan