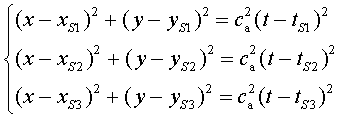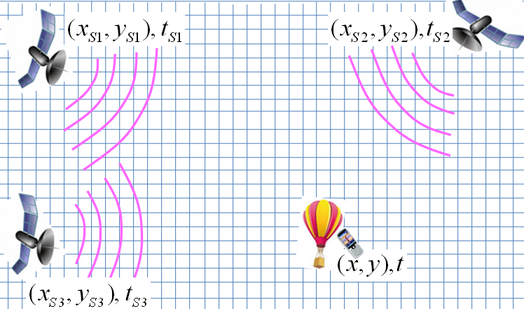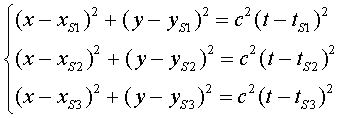 |
| Fig. 1: Global positioning system. |
Introducció
El sistema de localització GPS  (Global
Positioning System) és un sistema de navegació
per satèl•lit. Breument, podem dir que consta d'un mínim
de quatre satèl•lits en òrbita coneguda (posició
coneguda) cadascun dels quals porta un rellotge idèntic i
que estan sincronitzats. Aquest satèl•lits van enviant constantment
(cada mil•lisegon) senyals de ràdio amb la informació
sobre la seva posició i el temps que indiquen els seus rellotges.
Aquesta informació pot ser rebuda per qualsevol receptor.
És exactament com si es tractés de quatre emissores
de ràdio convencionals (RAC1, Catradio, SER...) amb un contingut
avorridíssim. Cada emissora-satèl•lit (Global
Positioning System) és un sistema de navegació
per satèl•lit. Breument, podem dir que consta d'un mínim
de quatre satèl•lits en òrbita coneguda (posició
coneguda) cadascun dels quals porta un rellotge idèntic i
que estan sincronitzats. Aquest satèl•lits van enviant constantment
(cada mil•lisegon) senyals de ràdio amb la informació
sobre la seva posició i el temps que indiquen els seus rellotges.
Aquesta informació pot ser rebuda per qualsevol receptor.
És exactament com si es tractés de quatre emissores
de ràdio convencionals (RAC1, Catradio, SER...) amb un contingut
avorridíssim. Cada emissora-satèl•lit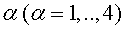 diu
" diu
"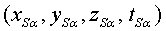 "
un cop cada mil·lisegon. Amb aquesta informació rebuda el
receptor pot saber la seva localització i el temps "
un cop cada mil·lisegon. Amb aquesta informació rebuda el
receptor pot saber la seva localització i el temps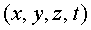 .
Com és això possible? És aquest sistema relativista...Perquè?
Vegem-ho una mica tot plegat. .
Com és això possible? És aquest sistema relativista...Perquè?
Vegem-ho una mica tot plegat.
El que volem és explicar l'essència del sistema GPS
de manera senzilla, poder veure quina és la idea bàsica
del seu funcionament, per la qual no cal apel•lar gaire a la relativitat.
Per això ens serà molt útil veure com funciona
el sonar i dissenyar un GPS acústic a l'aigua o a l'aire.
Per no embolicar i perquè el paper i la pantalla són bidimensionals,
posarem exemples en dues dimensions (2D). Així, ja des d'ara prescindim
de 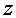 . .
 |
| Fig. 2: La pantalla d'un sonar. |
El sonar
El sonar 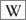 (sound navigation and ranging) és un dels sistemes de localització
més coneguts gràcies a les pel•lícules. El so rítmic del sonar, BIP-BIP-BIP,
l'hem sentit multitud de vegades en incomptables viatges submarins.
(sound navigation and ranging) és un dels sistemes de localització
més coneguts gràcies a les pel•lícules. El so rítmic del sonar, BIP-BIP-BIP,
l'hem sentit multitud de vegades en incomptables viatges submarins.
Ens situem al fons del mar, d'aigües absolutament tranquil•les
i homogènies. No hi ha corrents marins, no hi ha gradients de densitat ni de
temperatura.
Un submarí en la posició 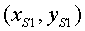 va
enviant senyals acústics, BIP-BIP, controlant en quina direcció va
enviant senyals acústics, BIP-BIP, controlant en quina direcció 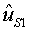 els
envia. Va registrant l'interval de temps de rebot del senyal els
envia. Va registrant l'interval de temps de rebot del senyal 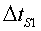 .
Si la velocitat del so a l'aigua és i el radar detecta un .
Si la velocitat del so a l'aigua és i el radar detecta un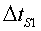 inusualment
curt, atribuïble a una roca propera en una posició no coneguda inusualment
curt, atribuïble a una roca propera en una posició no coneguda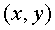 ,
tindrem que la distància entre el submarí i la roca serà igual a la velocitat
del so ,
tindrem que la distància entre el submarí i la roca serà igual a la velocitat
del so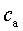 per
per 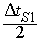 , ja que , ja que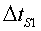 és el temps que triga el senyal a anar i tornar. El vector que va del submarí
a la roca és
és el temps que triga el senyal a anar i tornar. El vector que va del submarí
a la roca és 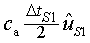 i,
per tant, podem escriure i,
per tant, podem escriure
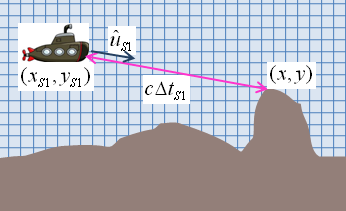 |
| Fig. 3: Funcionament d'un sonar. |
expressió que permet calcular la posició 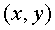 de
la roca. de
la roca.
Normalment al submarí només li interessa la posició
relativa de la roca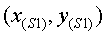
Un GPS acústic
Ens situem de nou al fons del mar, d'aigüess absolutament
tranquil•les i homogènies. No hi ha corrents marins, no hi ha gradients de densitat
ni de temperatura.
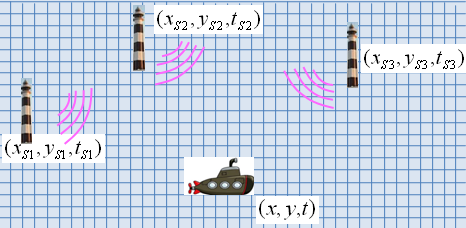 |
| Fig. 4: Un GPS acústic. |
Suposem que és el submarí, el que vol saber la
seva localització. Per a això té un sistema d'emissors
acústics, que en direm torres. En 2D es necessiten un mínim
de tres torres. Cada torre té un bon rellotge i els tres rellotges estan
sincronitzats, que per a nosaltres de moment vol dir que "indiquen
la mateixa hora". Una mica més avall tornarem sobre aquest punt.
Cada torre envia periòdicament un senyal acústic. Ara, enlloc
de fer BIP-BIP-BIP, els senyals acústics duen informació. Cada
torre, cada molt poc temps, envia un senyal que diu la seva posició i
el temps d'emissió: . 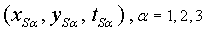 .
Si els senyals acústics viatgen a una velocitat .
Si els senyals acústics viatgen a una velocitat 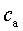 ,
en l'arribar al submarí es poden ajuntar les dades i raonar amb "senzillesa
no relativista" que la distància entre cada torre i el submaríés igual
a la velocitat del senyal per la diferència entre els temps de sortida i d'arribada: ,
en l'arribar al submarí es poden ajuntar les dades i raonar amb "senzillesa
no relativista" que la distància entre cada torre i el submaríés igual
a la velocitat del senyal per la diferència entre els temps de sortida i d'arribada:
Aquest sistema d'equacions permet trobar la posició del submarí,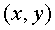 ,
a més del temps ,
a més del temps 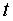 en
quèestà en aquesta posició. Aquest mètode té
molts avantatges respecte del sonar. Les torres envien senyals acústics
sense estar pendents de cap submarí en concret. Els senyals les potrebre
qualsevol submarí o qualsevol altre nau que tingui un receptor;només
ha de resoldre les equacions (3). Podem dir que és un
sistema multiusuari, sense limitacions quant a nombre d'usuaris, sempre que
cadascun porti el seu receptor....Compte! No resol el problema de la roca que
sí resol el sonar. en
quèestà en aquesta posició. Aquest mètode té
molts avantatges respecte del sonar. Les torres envien senyals acústics
sense estar pendents de cap submarí en concret. Els senyals les potrebre
qualsevol submarí o qualsevol altre nau que tingui un receptor;només
ha de resoldre les equacions (3). Podem dir que és un
sistema multiusuari, sense limitacions quant a nombre d'usuaris, sempre que
cadascun porti el seu receptor....Compte! No resol el problema de la roca que
sí resol el sonar.
En el cas del sonar tradicional fem el càlcul de l'espai recorregut
pel so com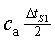 , on
apareix la diferència de temps d'un mateix rellotge. El càlcul es fa tenint
en compte que la velocitat del so i el temps que triga en l'anada i la tornada
són iguals. Ara, com a resultat del càlcul, trobem el temps , on
apareix la diferència de temps d'un mateix rellotge. El càlcul es fa tenint
en compte que la velocitat del so i el temps que triga en l'anada i la tornada
són iguals. Ara, com a resultat del càlcul, trobem el temps 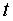 del
submarí en el moment de rebre els senyals. Aquest temps coincideix amb el temps
del rellotge que porta el submarí, si s'ha posat prèviament en hora.
Si no s'hi ha posat, ho es pot haver desajustat, es pot fer servir del
submarí en el moment de rebre els senyals. Aquest temps coincideix amb el temps
del rellotge que porta el submarí, si s'ha posat prèviament en hora.
Si no s'hi ha posat, ho es pot haver desajustat, es pot fer servir 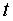 per ajustar el rellotge propi. Si comparem el càlcul (1) amb
(3) trobem que
per ajustar el rellotge propi. Si comparem el càlcul (1) amb
(3) trobem que 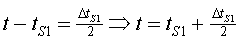 .
Això és que el temps de recepció del senyal per part del submaríés igual
al temps d'emissió més el temps que triga el senyal a anar de la torre al submarí.
Diem que .
Això és que el temps de recepció del senyal per part del submaríés igual
al temps d'emissió més el temps que triga el senyal a anar de la torre al submarí.
Diem que 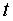 és un
temps sincronitzat amb és un
temps sincronitzat amb 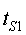 .
Això vol dir que, si tot roman en repòs, .
Això vol dir que, si tot roman en repòs, 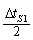 valdrà
sempre el mateix i quan el rellotge de la torre indiqui valdrà
sempre el mateix i quan el rellotge de la torre indiqui 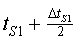 des
de la torre poden dir "ARA" i el submarí haurà rebut el senyal.
No només ho poden dir, sinó que ho poden comprovar fent una trucada
"instantània" feta amb un radiotransmissor (walkie-talkie).
Aquesta relació es donarà també amb els diferents rellotges
de les torres. Així, des
de la torre poden dir "ARA" i el submarí haurà rebut el senyal.
No només ho poden dir, sinó que ho poden comprovar fent una trucada
"instantània" feta amb un radiotransmissor (walkie-talkie).
Aquesta relació es donarà també amb els diferents rellotges
de les torres. Així, 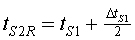 ,
on ,
on 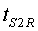 és el
temps de la torre és el
temps de la torre 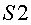 en
el moment del rebot del senyal enviat per en
el moment del rebot del senyal enviat per 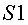 en
l'instant en
l'instant 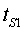 i que triga
a anar i tornar i que triga
a anar i tornar 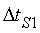 .
Aquesta operació de sincronització la podem fer amb so o amb algun altre agent
que compleixi que va i torna amb la mateixa velocitat. .
Aquesta operació de sincronització la podem fer amb so o amb algun altre agent
que compleixi que va i torna amb la mateixa velocitat.
Què pot fer que el sistema sonar i el GPS acústic
no funcionin tal com s'ha descrit? Perquè aquest mètode sigui
viable cal que la velocitat del so per l'aigua sigui rectilínia i uniforme,
tant en el camí d'anada com en el de tornada. Pot no ser així
a causa de gradients de temperatura o densitat. Però també a causa
que les aigües no estiguin tranquil•les. La presència de petits
corrents locals o grans corrents globals, encara que siguin uniformes, fan que
les expressions deixin de ser certes. En general, el mètode pot funcionar
amb algunes modificacions (per tenir en compte els gradients de densitat i temperatura)
i admet una resolució limitada. Modificar el sistema per tenir en compte
els corrents és difícil a causa de la seva variabilitat. És,
però, molt il•lustratiu imaginar que tenim un corrent global que fa que
tota l'aigua en bloc se'n vagi cap a la dreta a velocitat uniforme. En aquest
cas caldrà fer modificacions en el mètode per tenir en compte
la velocitat relativa del so respecte de les torres i el submarí,les
quals estan "previstes" per la física no relativista i no representen
cap problema conceptual.
Sincronitzar
Com sabem que dos rellotges en diferent lloc indiquen la mateixa
hora?. Què volem dir quan diem que indiquen la mateixa hora?... Quan
indiquen la mateixa hora?
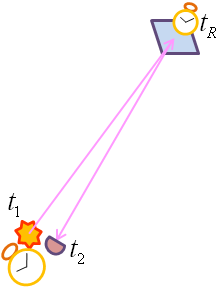 |
| Fig. 5: Sincronització de rellotges. |
L'Adelaida i en Joan fa temps que són parella, però
per raons laborals estan separats per la distància. L'Adelaida busca
la manera de sentir-se pròxima al Joan. L'Adelaida, de Sant Pere de Ribes,
molt clàssica ella, envia una postal de les d'abans al seu xicot,en Joan,
de Matadepera. A la postal,hi diu que quan la rebi li enviï de seguida
una altra postal a ella i que ella farà el mateix i així successivament.
En Joan no entén gaire de què van aquestes trifulgues de l'Adelaida,
però li fa cas, com sempre. L'Adelaida té una fe cega que el correu
triga el mateix a anar de Sant Pere a Matadepera que a tornar. Així,
quan rep la primera postal del Joan pot calcular quan en Joan estarà
escrivint les postalssegüents:
L'Adelaida, cada cop que el seu rellotge, el d'ella, indica
 s'emociona pensant
que ARA en Joan li està escrivint una postal. s'emociona pensant
que ARA en Joan li està escrivint una postal.
El que ha fet l'Adelaida és sincronitzar el seu rellotge
amb el del Joan, encara que aquest ni tan sols en té, de rellotge. D'aquesta
manera pot dir això que "ARA" sé que fa tal o qual cosa.
El mètode de sincronització que fa servir l'Adelaida és
certament primitiu. Però és essencialment el mateix que se li
va ocorre a Einstein per resoldre un conflicte semblant que tenia, no pas amb
la seva xicota, certament. Hi ha, però, algunes diferències entre
el que fa l'Adelaida i el que fa Einstein. L'Adelaida sempre pot comprovar el
moment "ARA", que ella ha calculat, en què espera que en Joan
escriu, fent-li una trucada. Einstein va constatar que, no havent-hi una manera
de comunicar-se a velocitat infinita, era del tot necessari per fer física
sincronitzar rellotges. L'anomenat protocol d'Einstein diu que dos
rellotges distants en repòs estan sincronitzats si el temps de recepció
d'un d'ells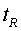 d'un
senyal lluminós enviat per l'altre al temps d'emissió d'un
senyal lluminós enviat per l'altre al temps d'emissió 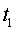 compleix compleix
on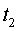 és
el temps de retorn del senyal emès (vegeu la figura). Aparentment i de
forma essencial, aquest protocol només difereix del de l'Adelaida enel
fet que utilitza una velocitat molt més gran que la del correu postal.
Però junt amb el principi de relativitat, Einstein requeria que aquest
mètode de sincronització fos realitzable en qualsevol sistema
de referències inercial. Ara,com que la llum és la màxima
velocitat possible, aquest mètode no admet cap comprovació "directa".
En tot cas, podrem treure'n conseqüències i veure si s'adiuen amb
la realitat. La "paradoxa" dels bessons és
el temps de retorn del senyal emès (vegeu la figura). Aparentment i de
forma essencial, aquest protocol només difereix del de l'Adelaida enel
fet que utilitza una velocitat molt més gran que la del correu postal.
Però junt amb el principi de relativitat, Einstein requeria que aquest
mètode de sincronització fos realitzable en qualsevol sistema
de referències inercial. Ara,com que la llum és la màxima
velocitat possible, aquest mètode no admet cap comprovació "directa".
En tot cas, podrem treure'n conseqüències i veure si s'adiuen amb
la realitat. La "paradoxa" dels bessons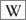 és una de les conseqüències més conegudes i comprovades.
és una de les conseqüències més conegudes i comprovades.
El GPS o sistema de navegació per satèl·lit
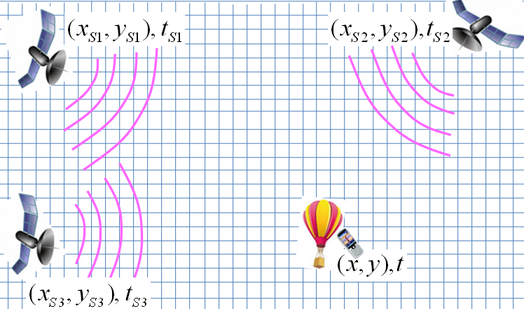 |
| Fig. 6: El GPS |
El sistema GPS instal·lat actualment en essència funciona
igual que el GPS acústic però amb llum (ones electromagnètiques).
En 2D es necessiten un mínim de tres satèl•lits. També requereix que
els rellotges dels satèl•lits estiguin sincronitzats segons el protocol
d'Einstein. En aquestes condicions cada satèl•lit envia un cop cada mi·lisegon
informació sobre la seva posició i el seu temps, 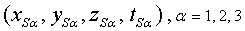 ,
en totes les direccions de l'espai, com si fossin emissores de ràdio.
Les persones del globus de la figura tenen un receptor preparat per rebre simultàniament
les emissions dels 3 satèl•lits. Amb tota aquesta informació i
gràcies a la sincronització, tenim: ,
en totes les direccions de l'espai, com si fossin emissores de ràdio.
Les persones del globus de la figura tenen un receptor preparat per rebre simultàniament
les emissions dels 3 satèl•lits. Amb tota aquesta informació i
gràcies a la sincronització, tenim:
D'aquestes equacions podem trobar 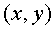 i i . .
Com veiem, no sembla que hi hagi gaires diferències formals
en les expressions. Els sistemes d'equacions (3) i (6)
són clavats, amb la excepció que a (3) 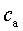 és
la velocitat del so per a l'aigua i a (6) és
la velocitat del so per a l'aigua i a (6)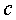 és
la velocitat de la llum en el buit. No és només un canvi de numeret. és
la velocitat de la llum en el buit. No és només un canvi de numeret. 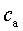 es propaga pel medi aigua i és una velocitat relativament discreta. Se'n coneixen
de més ràpides, per exemple la llum.
es propaga pel medi aigua i és una velocitat relativament discreta. Se'n coneixen
de més ràpides, per exemple la llum. 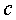 es
propaga pel buit, que no és un medi, i no se'n coneix cap de més ràpida. es
propaga pel buit, que no és un medi, i no se'n coneix cap de més ràpida.
Com en el cas del GPS acústic, com a resultat del càlcul trobem
el temps 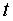 del globus
en el moment de rebre els senyals. Aquest temps coincideix amb el temps del
rellotge que porta el globus, si s'ha posat prèviament en hora. Si no
l'hi ha posat o se li pot haver desajustat pot fer servir del globus
en el moment de rebre els senyals. Aquest temps coincideix amb el temps del
rellotge que porta el globus, si s'ha posat prèviament en hora. Si no
l'hi ha posat o se li pot haver desajustat pot fer servir 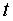 per ajustar el rellotge propi. Podem tornar a considerar
per ajustar el rellotge propi. Podem tornar a considerar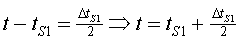 .
Això és que el temps de recepció del senyal per part del globus és igual al
temps d'emissió més el temps que triga el senyal a anar del satèl•lit
al globus. Diem que .
Això és que el temps de recepció del senyal per part del globus és igual al
temps d'emissió més el temps que triga el senyal a anar del satèl•lit
al globus. Diem que 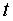 és
un temps sincronitzat amb és
un temps sincronitzat amb 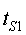 :
si tot roman en repòs, :
si tot roman en repòs, 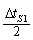 valdrà
sempre el mateix; quan el rellotge del satèl•lit indiqui valdrà
sempre el mateix; quan el rellotge del satèl•lit indiqui 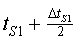 des
del satèl•lit poden dir que "ara" el globus ha rebut elsenyal.
Ara però no poden comprovar-ho fent una trucada pel walkie-talkie! des
del satèl•lit poden dir que "ara" el globus ha rebut elsenyal.
Ara però no poden comprovar-ho fent una trucada pel walkie-talkie!
En el cas del GPS acústic, hem comentat que si l'aigua
no romangués en repòs hauríem de fer modificacions en el
mètode. Aquestes modificacions estan previstes per la física no
relativista i no hi ha cap problema conceptual per implementar-les.És
tan sols una qüestió "tècnica".
Quin és ara l'equivalent del fet que "les aigües no estiguin
tranquil•les"? Doncs en principi la constància de la velocitat de
la llum és vàlida en un sistema inercial. Aigües tranquil•les
vol dir sistema inercial. Dos sistemes inercials diferents, un que podem considerar
quiet i un altre en moviment uniforme, són els dos "aigües
tranquil•les ". La teoria que fa compatible que per a dos sistemes inercials
diferents la llum, més exactament el mateix focus de llum per als dos,
vagi a la mateixa velocitat, és la relativitat especial. Això
vol dir que no ens hem de preocupar per si el nostre sistema de referència
inercial està o no en moviment. Les equacions que farem servir són
les descrites més amunt. Per exemple, en el cas de la translació
de la Terra al voltant del Sol, sempre que per als intervals de temps amb què
treballem el puguem tractar com a moviment uniforme, no ens afectarà
per res el mètode. La cosa s'embolica quan constatem que la rotació
de la Terra, i també la gravetat, fan que el sistema GPS pugui no ser
un "bon sistema inercial". Les modificacions que cal fer no pertanyen
a la física no relativista. No estaven previstes. Cal tractar aquestes
modificacions en el marc de la relativitat general. I això amb prou feines
se sap fer avui en dia! Des d'aquest punt de vista, el sistema GPS és
un sistema de localització relativista. Però en una primera aproximació,
si no volem una gran resolució i nosaltres estem en repòs, o ens
movem a baixes velocitats respecte de la llum, podem considerar el sistema GPS
com a inercial i fer servir les equacions (6) per trobar la
localització i el temps d'on som, 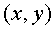 i i exactament igual que fem amb el GPS acústic.
exactament igual que fem amb el GPS acústic.
Si podem considerar el sistema de satèl•lits GPS com
a inercial i el receptor GPS està en repòs o es mou a velocitats relativament
baixes, el mètode no difereix en essència de la localització amb el GPS
acústic. Cal tenir en compte que un error d'un microsegon (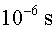 )
en la mesura dels temps comporta un error d'uns )
en la mesura dels temps comporta un error d'uns 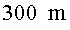 en
la localització amb el GPS amb llum. En el cas del GPS acústic un error
d'un mil·lisegon ( en
la localització amb el GPS amb llum. En el cas del GPS acústic un error
d'un mil·lisegon (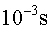 )
en la mesura del temps comporta "només" un error d' )
en la mesura del temps comporta "només" un error d' 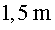 en
la localització. Un dels requeriments essencials del sistema GPS és que els
rellotges romanguin sincronitzats, entre ells, amb llum. Com és que ens
entestem a fer servir la llum si el fet de ser tan ràpida fa que cometem
tant error?. És cert que el fet de ser tan ràpida ens fa cometre
un tipus d'error deguts a la mesura del temps, però en canvi el fet que
la coneguem amb gran precisió, en
la localització. Un dels requeriments essencials del sistema GPS és que els
rellotges romanguin sincronitzats, entre ells, amb llum. Com és que ens
entestem a fer servir la llum si el fet de ser tan ràpida fa que cometem
tant error?. És cert que el fet de ser tan ràpida ens fa cometre
un tipus d'error deguts a la mesura del temps, però en canvi el fet que
la coneguem amb gran precisió, 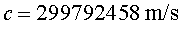 ,
fa que, respecte al coneixement poc fiable dels senyals acústics i d'altres,
la llum sigui un bon agent de transmissió. A més, la llum viatja
a una velocitat sensiblement constant per l'atmosfera i...pot viatjar pel buit! ,
fa que, respecte al coneixement poc fiable dels senyals acústics i d'altres,
la llum sigui un bon agent de transmissió. A més, la llum viatja
a una velocitat sensiblement constant per l'atmosfera i...pot viatjar pel buit!

|

 8/8
8/8