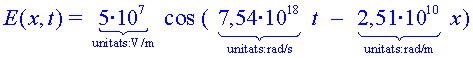Buscant una mica podem trobar molts contextos que mostren, de nou, que la física que estudien els nostres alumnes és rellevant per al món que els envolta; que val la pena fer l’esforç d’acostar l’aula a les aplicacions i desenganxar-los una mica de problemes que només viuen sobre el paper.
En el primer exemple, encara que seria possible trobar-ne molts d’aplicats als tubs de raigs catòdics de televisió (aquí el currículum ha quedat molt ràpidament antiquat!) , s’ha buscat una situació equivalent encara que menys coneguda.  
Full de l'alumnat
Els problemes
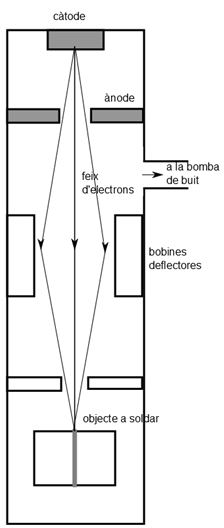 |
| Fig. 1: Dispositiu de soldadura per feix d'electrons |
| El camp elèctric
1: Descripció del funcionament
d'un tub de raigs catòdics de televisió. Reconeixement
quantitatiu de la transformació de l'energia en un canó
d'electrons. Comparació de la transformació de l'energia
en un canó d'electrons i la que es produeix en un camp gravitatori
uniforme.
|
1. La figura 1 mostra
el funcionament d'un dispositiu de soldadura per feix d'electrons. La diferència
de potencial entre el càtode (d'on surten els electrons amb una velocitat
molt petita) i l'ànode és de 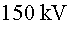 .
El feix d'electrons es dirigeix al punt on volem fer la soldadura, on xoquen
i fonen les superfícies que s'han de soldar, amb potències de
fins a .
El feix d'electrons es dirigeix al punt on volem fer la soldadura, on xoquen
i fonen les superfícies que s'han de soldar, amb potències de
fins a 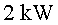 . Quan el metall
es refreda torna a solidificar i les superfícies queden unides de manera
molt forta. . Quan el metall
es refreda torna a solidificar i les superfícies queden unides de manera
molt forta.
a) En quines regions
del dispositiu guanyen energia cinètica els electrons? En quines regions
en perden?
b) Quina funció tenen les bobines
deflectores? Proposa un mecanisme perquè funcionin.
c) Una bomba de buit manté tot
l'aparell a una pressió baixíssima. Què passaria si hi
hagués aire dins del dispositiu?
d) Calcula l'energia cinètica
dels electrons en passar per l'ànode i en xocar amb l'objecte que s'ha
de soldar. Quina velocitat tenen aquests electrons?
e) Quants electrons han de cedir la
seva energia cinètica cada segon per subministrar els 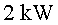 de potència a la zona que s'ha de soldar? Expressa el resultat en nombre
d'electrons i també com a intensitat de corrent elèctric (en
ampers).
de potència a la zona que s'ha de soldar? Expressa el resultat en nombre
d'electrons i també com a intensitat de corrent elèctric (en
ampers).
Dades:
| El camp elèctric
2: Caracterització del
model d'interacció a través d'un camp com a alternativa
al model d'interacció a distància. Característiques
del camp elèctric: intensitat del camp elèctric com a
força per unitat de càrrega. 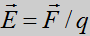 ,
caràcter vectorial del camp elèctric. Comparació
amb el camp gravitatori. ,
caràcter vectorial del camp elèctric. Comparació
amb el camp gravitatori.
|
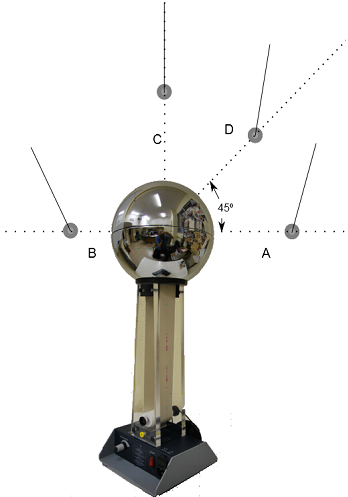 |
| Fig. 2: Generador de Van der Graaff |
2. En una demostració
en un taller d'electrostàtica es carrega una esfera metàl•lica
fins a un voltatge molt alt. Per explorar el camp elèctric al voltant
de l'esfera hi acostem una petita bola de 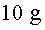 que penja d'un fil molt lleuger de
que penja d'un fil molt lleuger de 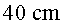 de llarg. Sabem que la boleta té una càrrega elèctrica
de
de llarg. Sabem que la boleta té una càrrega elèctrica
de 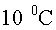 . .
Quan situem la boleta en diferents punts (A,B,C
i D) veiem, en la
figura 2, que en cada cas el fil pren una inclinació diferent: situada
en el punt A la inclinació
és de 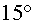 , mentre
que quan la situem en el punt B
la inclinació és de , mentre
que quan la situem en el punt B
la inclinació és de 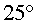 . .
a) Dibuixa els diagrames
de forces per a cada una de les 4
posicions.
b) Dibuixa, qualitativament,
els vectors de camp elèctric en cada un dels 4
punts explorats.
c) Calcula el camp
elèctric en els punts A
i B.
d) Considera que en
el punt D el mòdul
del camp elèctric és el mateix que en el punt A,
però que la direcció difereix 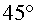 .
Calcula la inclinació del fil quan la boleta està en el punt
D. .
Calcula la inclinació del fil quan la boleta està en el punt
D.
| El camp elèctric
3: Identificació del potencial
elèctric com a energia potencial elèctrica per unitat
de càrrega i del seu caràcter escalar. Reconeixement de
línies de camp i superfícies equipotencials. Utilització
de simulacions per visualitzar-les. Determinació experimental
de superfícies equipotencials.
|
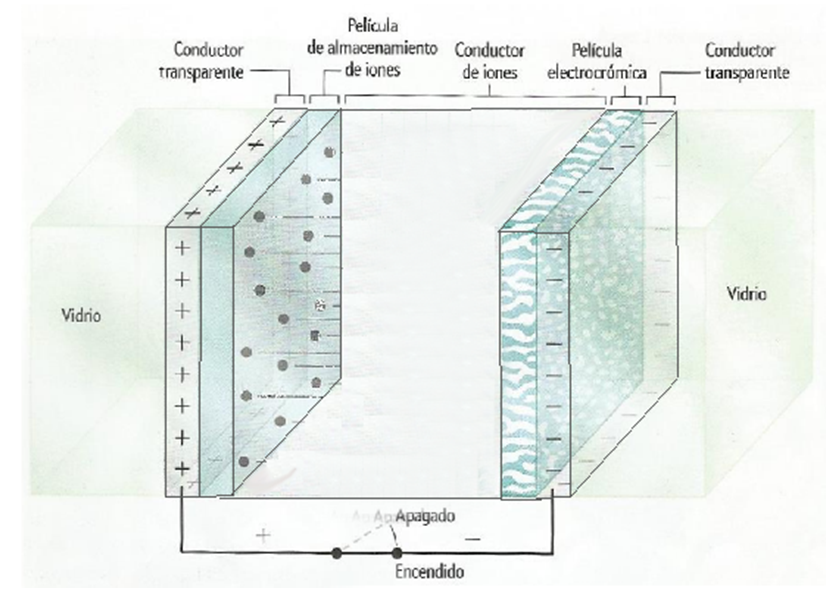 |
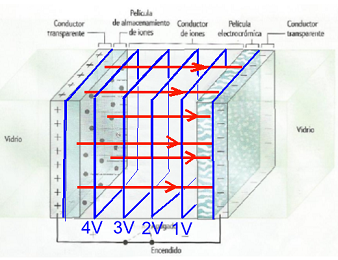
| Fig. 3: Estructura d'un material electrocròmic. Origen
de la imatge: Investigación y Ciencia, desembre
de 2013 |
3.La figura 3 mostra
l’estructura d’un material electrocròmic. El color d’aquest
material es pot modificar a voluntat quan una diferència de potencial
entre les plaques de material conductor desplaça els ions fins a la pel•lícula
electrocròmica.
Considera que la distància entre les plaques conductores
és de 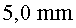 , que la
diferència de potencial entre les plaques és de , que la
diferència de potencial entre les plaques és de 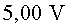 i que el camp elèctric entre les plaques és aproximadament constant.
Atribuirem
i que el camp elèctric entre les plaques és aproximadament constant.
Atribuirem 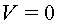 a la placa
negativa. Els ions estan inicialment a a la placa
negativa. Els ions estan inicialment a 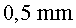 de la placa positiva.
de la placa positiva.
a) Dibuixa les línies
de camp i les superfícies equipotencials corresponents a 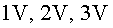 i
i 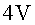 . .
b) Troba l'energia potencial de cada
un dels ions (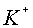 i i 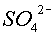 )
en la seva posició inicial. )
en la seva posició inicial.
c) Calcula el treball fet pel camp
elèctric quan cada un dels ions (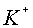 i
i 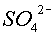 ) va des de la seva
posició inicial fins a la placa que té el signe contrari a la
seva càrrega. Indica el resultat en joules (J)
i en electronvolts (eV). ) va des de la seva
posició inicial fins a la placa que té el signe contrari a la
seva càrrega. Indica el resultat en joules (J)
i en electronvolts (eV).
Dades: càrrega 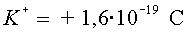 ;
càrrega ;
càrrega 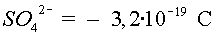 ; ;
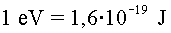 . .
| El camp elèctric
4: Relació entre força
i gradient d'energia potencial i entre camp i gradient de potencial
per a un camp elèctric uniforme. Aplicacions de la desviació
de partícules carregades que es mouen en el si de camps elèctrics
uniformes: acceleradors lineals i circulars. Comparació amb la
desviació de masses que es mouen en un camp gravitatori uniforme.
|
4.4. La figura 4 mostra
les superfícies equipotencials sota un núvol, en un terreny pla
amb una torre metàl•lica de 20
metres d’altura.
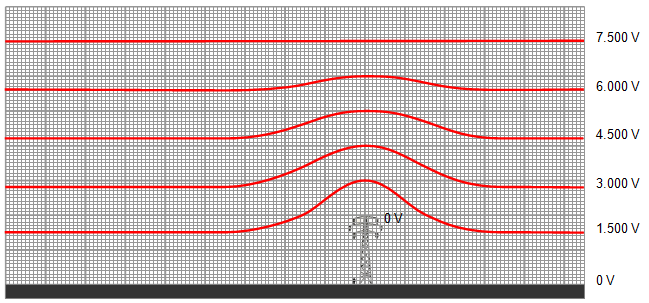 |
| Fig. 4: Superfícies equipotencials |
a) Dibuixa, de manera
aproximada les línies de camp elèctric en aquesta zona i indica
el signe de les càrregues al terra i a la part inferior del núvol.
b) Indica on és més intens
el camp elèctric i calcula’n el valor.
c) Compara l’energia que es despendrà
en un llamp que vagi del núvol i al terra i un llamp (de la mateixa
càrrega) que vagi del núvol a la punta de la torre.
5. Utilitzant un programa
de simulació hem enviat una partícula (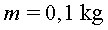 , ,
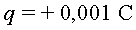 , , 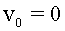 )
a través de tres zones, cada una amb el seu camp elèctric uniforme
i constant. S'han pres imatges de la partícula cada )
a través de tres zones, cada una amb el seu camp elèctric uniforme
i constant. S'han pres imatges de la partícula cada 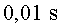 i
hem obtingut la figura 5 (les posicions estan indicades en metres): i
hem obtingut la figura 5 (les posicions estan indicades en metres):
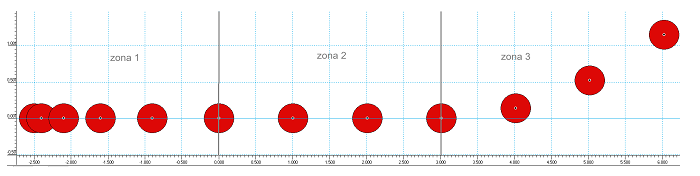 |
| Fig. 5: Posicions d'una partícula carregada en moviment. |
a) Determina la direcció
, sentit i intensitat del camp elèctric en cada una de les zones.
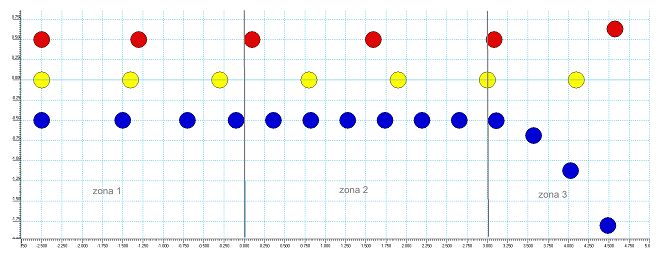
b) En la següent imatge (figura
6) veiem tres partícules amb diferent càrrega elèctrica
però amb la mateixa massa, que entren a la mateixa velocitat en la
mateixa regió de l'espai de l'apartat anterior. Identifica el signe
de cada una de les càrregues i explica el diferent comportament que
mostren.
 |
|
Fig. 6: Moviment de tres partícules amb diferent càrrega
però la mateixa massa. |
c) En la tercera imatge
(figura 7) tenim tres partícules amb la mateixa càrrega elèctrica
però amb diferents masses. Ordena les partícules segons la seva
massa i justifica'n el diferent comportament.
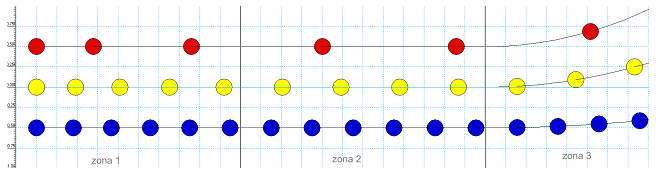 |
| Fig. 7: Moviment de partícules amb la mateixa
càrrega però masses diferents. |
d) Si en comptes de
camps elèctrics haguéssim fet les simulacions amb camps gravitatoris,
quines diferències hi hauríem trobat?
| El camp elèctric
5: Descripció del detector
Geiger-Muller, per a la introducció a l'estudi de camps elèctrics
no uniformes amb simetria cilíndrica i esfèrica. Anàlisi
de la dependència de la intensitat del camp amb la distància
a partir de consideracions de simetria.
|
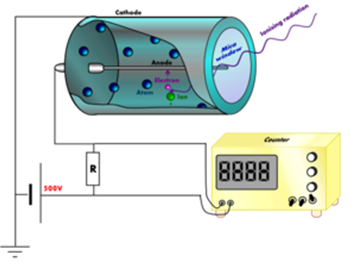 |
| Fig. 8: Tub de Geiger. Imatge extreta de la Wikipedia ("Geiger-Müller
tube") |
6.Observa la figura 8 que representa
un tub de Geiger.
a) Dibuixa, de manera
aproximada, les línies de camp i les superfícies equipotencials
a l'interior d'un tub de Geiger format per un fil positiu (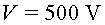 )
i un cilindre coaxial negatiu ( )
i un cilindre coaxial negatiu (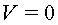 ).
Raona si la superfície equipotencial ).
Raona si la superfície equipotencial 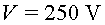 estarà més a prop del fil o més a prop del cilindre.
estarà més a prop del fil o més a prop del cilindre.
b) Compara el nombre de línies
de camp que travessen cada una de les superfícies equipotencials.
c) On és més intens el
camp? Compara la intensitat del camp elèctric en dos punts situats
a 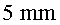 i i 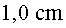 de l'eix central, respectivament.
de l'eix central, respectivament.
| El camp elèctric
6: Caracterització del
camp elèctric (intensitat i potencial) creat per càrregues
puntuals. Llei de Coulomb.
|
7.Una antena consisteix en un pal
metàl•lic vertical de 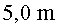 d’altura en el qual les càrregues elèctriques es mouen
d’un extrem a l'altre. En un moment donat hi ha una càrrega de
d’altura en el qual les càrregues elèctriques es mouen
d’un extrem a l'altre. En un moment donat hi ha una càrrega de
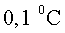 a l’extrem
superior i de a l’extrem
superior i de 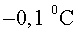 al
nivell de terra. Considera el punt P
situat al terra, a 10
metres de la base de l’antena. al
nivell de terra. Considera el punt P
situat al terra, a 10
metres de la base de l’antena.
a) Fes un esquema
de la situació i dibuixa els vectors del camp elèctric causat
per cada una de les càrregues en el punt P.
b) Calcula el camp elèctric
total en aquest punt.
c) Calcula el potencial elèctric
en el punt P.
d) Calcula els valors de la intensitat
del camp i del potencial un instant més tard, quan les dues càrregues
de l’antena hagin permutat les posicions.
Dades: càrrega  . .
| Relació
entre el camp elèctric i magnètic i síntesi electromagnètica
de Maxwell. Caracterització de les ones electromagnètiques.
|
8.La figura 9 mostra un ondulador.
Els onduladors són essencialment una regió en la que les partícules
carregades es troben successivament camps magnètics de sentit alternat
que s'utilitzen com a font de radiació molt intensa en els sincrotrons.
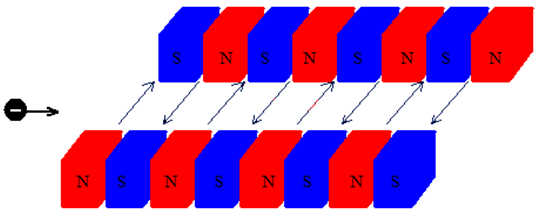 |
| Fig. 9: Esquema d'un ondulador d'un sincrotró. |
a) Considera que l'electró
arriba a l'ondulador des de l'esquerra i el travessa completament. Dibuixa
de manera aproximada la trajectòria que seguirà.
Les figures 10a i 10b mostren el camp elèctric
causat per l'electró abans d'entrar en l'ondulador, quan l'electró
es mou amb un moviment rectilini uniforme (MRU) i quan l'electró es mou
dins de l'ondulador
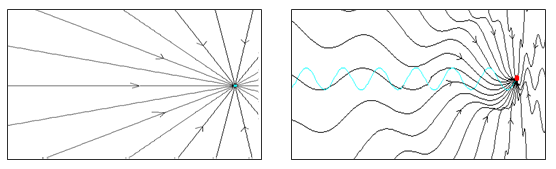 |
| Fig. 10a i b: Camp elèctric de l'electró
abans d'entrar (a) i dins (b) de l'ondulador |
b) Com pots relacionar aquesta informació
amb la producció d’ones electromagnètiques en l’ondulador?
c) Ens informen que un ondulador produeix
raigs-X pràcticament
unidireccionals d'una longitud d'ona 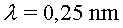 amb una amplitud del camp elèctric de
amb una amplitud del camp elèctric de 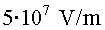 .
Escriu l'equació de l'ona plana .
Escriu l'equació de l'ona plana 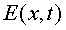 d'aquests
raigs-X (pots ignorar-ne
la fase inicial). d'aquests
raigs-X (pots ignorar-ne
la fase inicial).

 
Solucions
1.La figura 1 mostra
el funcionament d'un dispositiu de soldadura per feix d'electrons. La diferència
de potencial entre el càtode (d'on surten els electrons amb una velocitat
molt petita) i l'ànode és de 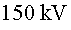 .
El feix d'electrons es dirigeix al punt on volem fer la soldadura, on xoquen
i fonen les superfícies que s’han de soldar, amb potències
de fins a .
El feix d'electrons es dirigeix al punt on volem fer la soldadura, on xoquen
i fonen les superfícies que s’han de soldar, amb potències
de fins a 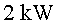 . Quan el
metall es refreda torna a solidificar i les superfícies queden unides
de manera molt forta. . Quan el
metall es refreda torna a solidificar i les superfícies queden unides
de manera molt forta.
a) En quines regions
del dispositiu guanyen energia cinètica els electrons? En quines regions
en perden?
En guanyen: entre el càtode i l'ànode.
En perden: en xocar amb la superfície metàl•lica.
b) Quina funció tenen les bobines
deflectores? Proposa un mecanisme perquè funcionin.
Desvien els electrons. Podrien fer-ho uns camps magnètics
(uns imants o electroimants) amb la direcció del camp tangencial o
uns camps elèctrics (plaques amb diferència de potencial (ddp))
amb la direcció del camp radial.
c) Una bomba de buit manté tot
l'aparell a una pressió baixíssima. Què passaria si hi
hagués aire dins del dispositiu?
Els electrons perdrien energia pel camí (i es
desviarien) en xocar amb les molècules residuals. Les trajectòries
serien impredictibles.
d) Calcula l'energia cinètica
dels electrons en passar per l'ànode i en xocar amb l'objecte que s’ha
de soldar. Quina velocitat tenen aquests electrons?
En passar per l'ànode (i abans de xocar) 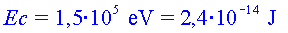 ;
;  (resultat no relativista)
i (resultat no relativista)
i 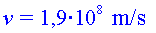 (resultat relativista). (resultat relativista).
e) Quants electrons
han de cedir la seva energia cinètica cada segon per subministrar els
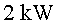 de potència
a la zona que s’ha de soldar? Expressa el resultat en nombre d'electrons
i també com a intensitat de corrent elèctric (en ampers (A)). de potència
a la zona que s’ha de soldar? Expressa el resultat en nombre d'electrons
i també com a intensitat de corrent elèctric (en ampers (A)).

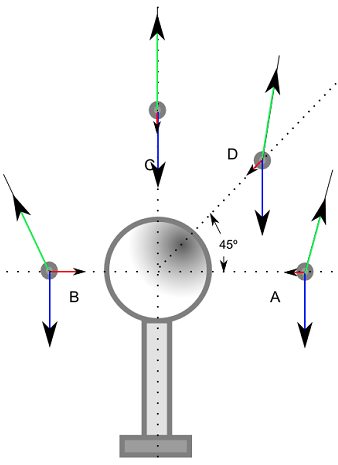 |
| Fig. 11: |
2.En una demostració
en un taller d'electrostàtica es carrega una esfera metàl•lica
fins a un voltatge molt alt. Per explorar el camp elèctric al voltant
de l'esfera hi acostem una petita bola de 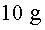 que penja d'un fil molt lleuger de
que penja d'un fil molt lleuger de 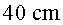 de llarg. Sabem que la boleta té una càrrega elèctrica
de
de llarg. Sabem que la boleta té una càrrega elèctrica
de 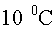 . .
Quan situem la boleta en diferents punts (A,B,C
i D) veiem, en la
figura 2, que en cada cas el fil pren una inclinació diferent: situada
en el punt A la inclinació
és de 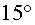 , mentre
que quan la situem en el punt B
la inclinació és de , mentre
que quan la situem en el punt B
la inclinació és de 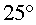 . .
a) Dibuixa els diagrames
de forces per a cada una de les 4
posicions.
A la figura 11: en verd: tensió; en blau: pes;
en vermell: força elèctrica.
b) Dibuixa, qualitativament,
els vectors camp elèctric en cada un dels 4
punts explorats.
El camp elèctric té la mateixa direcció
i sentit, i és proporcional a les forces elèctriques de l'apartat
anterior.
c) Calcula el camp
elèctric en els punts A
i B.
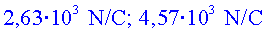
d) Considera que en
el punt D el mòdul
del camp elèctric és el mateix que en el punt A,
però que la direcció difereix 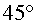 .
Calcula la inclinació del fil quan la boleta està en el punt
D. .
Calcula la inclinació del fil quan la boleta està en el punt
D.
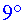
 |
| Fig. 12: |
3.La figura 3 mostra
l’estructura d’un material electrocròmic. El color d’aquest
material es pot modificar a voluntat quan una diferència de potencial
entre les plaques de material conductor desplaça els ions fins a la pel•lícula
electrocròmica.
Considera que la distància entre les plaques conductores
és de 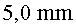 , que la
diferència de potencial entre les plaques és de , que la
diferència de potencial entre les plaques és de 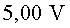 i que el camp elèctric entre les plaques és aproximadament constant.
Atribuirem
i que el camp elèctric entre les plaques és aproximadament constant.
Atribuirem 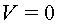 a la placa
negativa. Els ions estan inicialment a 0 a la placa
negativa. Els ions estan inicialment a 0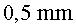 de la placa positiva.
de la placa positiva.
a) Dibuixa les línies
de camp i les superfícies equipotencials corresponents a 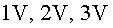 i
i 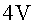 . .
A la figura 12
b) Troba l'energia potencial de cada
un dels ions ( i i 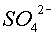 )
en la seva posició inicial. )
en la seva posició inicial.
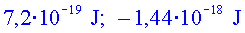
c) Calcula el treball fet pel camp
elèctric quan cada un dels ions ( i
i 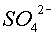 ) va des de la seva
posició inicial fins a la placa que té el signe contrari a la
seva càrrega. Indica el resultat en joules (J)
i en electronvolts (eV). ) va des de la seva
posició inicial fins a la placa que té el signe contrari a la
seva càrrega. Indica el resultat en joules (J)
i en electronvolts (eV).
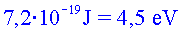 ; ;
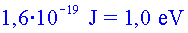 . .
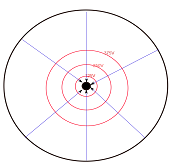
4. La figura 4 mostra
les superfícies equipotencials sota un núvol, en un terreny pla
amb una torre metàl•lica de 20
metres d’altura.
a) Dibuixa, de manera
aproximada, les línies de camp elèctric en aquesta zona i indica
el signe de les càrregues al terra i a la part inferior del núvol.
Vegeu la figura 13. La càrrega és positiva
a dalt i negativa al terra.
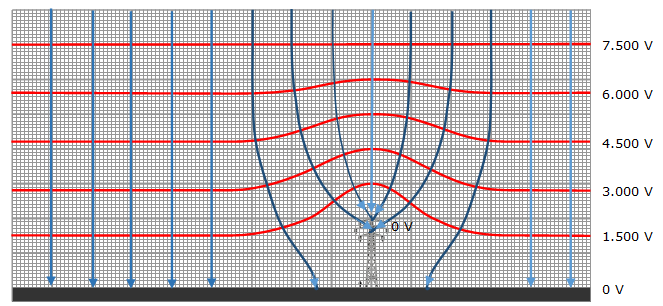 |
| Fig. 13: |
b) Indica on és més intens
el camp elèctric i calcula’n el valor.
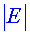 màxim
a la vertical sobre la torre, màxim
a la vertical sobre la torre, 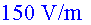 (cap
avall). (cap
avall).
c) Compara l’energia que es despendrà
en un llamp que vagi del núvol i al terra i un llamp (de la mateixa
càrrega) que vagi del núvol a la punta de la torre.
Seran iguals.
5. Utilitzant un programa
de simulació hem enviat una partícula (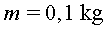 , ,
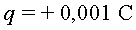 , , 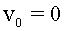 )
a través de tres zones, cada una amb el seu camp elèctric uniforme
i constant. S'han pres imatges de la partícula cada )
a través de tres zones, cada una amb el seu camp elèctric uniforme
i constant. S'han pres imatges de la partícula cada 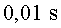 i
hem obtingut la figura 5 (les posicions estan indicades en metres): i
hem obtingut la figura 5 (les posicions estan indicades en metres):
a) Determina la direcció
, sentit i intensitat del camp elèctric en cada una de les zones.
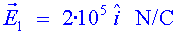 ; ;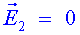 ; ;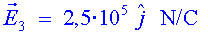
b) En la següent imatge (figura
6) veiem tres partícules amb diferent càrrega elèctrica
però amb la mateixa massa, que entren a la mateixa velocitat en la
mateixa regió de l'espai de l'apartat anterior. Identifica el signe
de cada una de les càrregues i explica el diferent comportament que
mostren.
La partícula groga no té càrrega.
La partícula blava és negativa i la vermella positiva... (per
cert, el valor absolut de les càrregues blava i vermella és
igual!).
c) En la tercera imatge
(figura 7) tenim tres partícules amb la mateixa càrrega elèctrica
però amb diferents masses. Ordena les partícules segons la seva
massa i justifica'n el diferent comportament.
Massa blava >
massa groga >
massa vermella.
d) Si en comptes de
camps elèctrics haguéssim fet les simulacions amb camps gravitatoris,
quines diferències hi hauríem trobat?
No podria haver-hi partícules amb massa negativa.
El moviment de les partícules només dependria del camp (i també
de la posició i la velocitat inicial), però no de la massa de
la partícula.
 |
| Fig. 14: |
6.Observa la figura 8 que representa
un tub de Geiger.
a) Dibuixa, de manera
aproximada, les línies de camp i les superfícies equipotencials
a l'interior d'un tub de Geiger format per un fil positiu (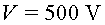 )
i un cilindre coaxial negatiu ( )
i un cilindre coaxial negatiu (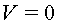 ).
Raona si la superfície equipotencial ).
Raona si la superfície equipotencial 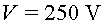 estarà més a prop del fil o més a prop del cilindre.
estarà més a prop del fil o més a prop del cilindre.
Més a prop del fil.
b) Compara el nombre de línies
de camp que travessen cada una de les superfícies equipotencials.
El mateix nombre de línies.
c) On és més intens el
camp? Compara la intensitat del camp elèctric en dos punts situats
a 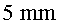 i i 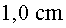 de l'eix central, respectivament.
de l'eix central, respectivament.
Prop del fil; |
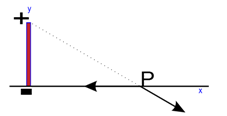 |
| Fig. 15: |
7.Una antena consisteix en un pal metàl•lic
vertical de 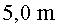 d’altura
en el qual les càrregues elèctriques es mouen d’un extrem
a l'altre. En un moment donat hi ha una càrrega de d’altura
en el qual les càrregues elèctriques es mouen d’un extrem
a l'altre. En un moment donat hi ha una càrrega de 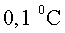 a l’extrem superior i de
a l’extrem superior i de 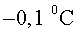 al nivell de terra. Considera el punt P
situat al terra, a 10 metres
de la base de l’antena.
al nivell de terra. Considera el punt P
situat al terra, a 10 metres
de la base de l’antena.
a) Fes un esquema
de la situació i dibuixa els vectors del camp elèctric causat
per cada una de les càrregues en el punt P.
Vegeu la figura 15.
b) Calcula el camp elèctric
total en aquest punt.
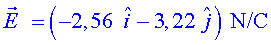
c) Calcula el potencial elèctric
en el punt P.
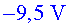
d) Calcula els valors de la intensitat
del camp i del potencial un instant més tard, quan les dues càrregues
de l’antena hagin permutat les posicions.
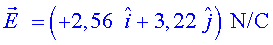 ;
;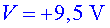
8.La figura 9 mostra un ondulador. Els
onduladors són essencialment una regió en la qual les partícules
carregades es troben successivament camps magnètics de sentit alternat
que s'utilitzen com a font de radiació molt intensa en els sincrotrons.
a) Considera que l'electró
arriba a l'ondulador des de l'esquerra i el travessa completament. Dibuixa
de manera aproximada la trajectòria que seguirà.
Vegeu la figura 16. Ep! Noteu que l'ondulació
és en el pla vertical.
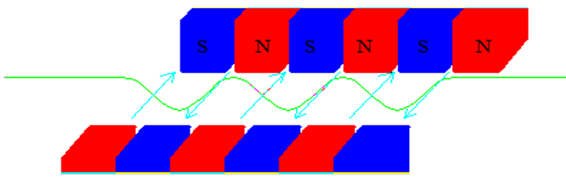 |
| Fig. 16: |
Les figures 10a i 10b mostren el camp elèctric
causat per l'electró abans d'entrar a l'ondulador, quan l'electró
es mou amb un moviment rectilini uniforme (MRU) i quan l'electró es mou
dins de l'ondulador
b) Com pots relacionar aquesta informació
amb la producció d’ones electromagnètiques en l’ondulador?
Quan l’electró es mou en l’ondulador
produeix un camp amb periodicitat en l’espai (es veu a la figura 16)
i, si imaginem l’electró desplaçant-se i “arrossegant”
el camp elèctric, amb periodicitat en el temps. Vet aquí una
ona. En la situació de MRU no s’aprecia cap periodicitat en el
camp elèctric.
c) Ens informen que un ondulador produeix
raigs-X pràcticament
unidireccionals d'una longitud d'ona 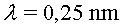 amb una amplitud del camp elèctric de
amb una amplitud del camp elèctric de 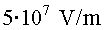 .
Escriu l'equació de l'ona plana .
Escriu l'equació de l'ona plana 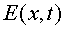 d'aquests
raigs-X (pots ignorar-ne
la fase inicial). d'aquests
raigs-X (pots ignorar-ne
la fase inicial).
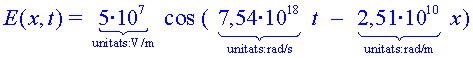

| 
 7/8
7/8