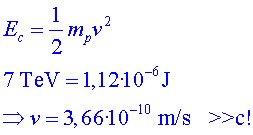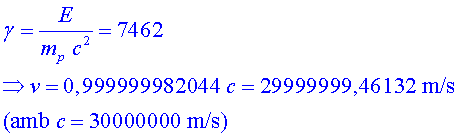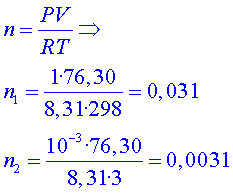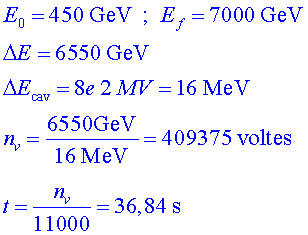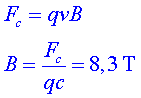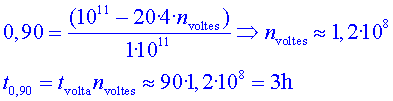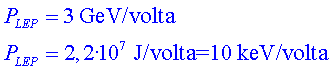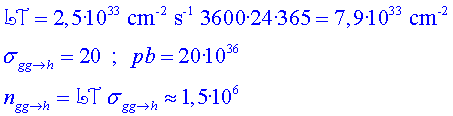Orientacions per al professorat
Temporització
- Tot i que cada secció es pot resoldre independentment, la total
comprensió d'alguns conceptes pot requerir haver estudiat els anteriors,
de manera que el recurs es presenta de manera seqüencial.
Alumnes als quals s’adreça l’experiència
- El conjunt dels conceptes està orientat a alumnes de segon de batxillerat
pel sol fet que ja han vist molts dels conceptes o poden entendre els nous
més ràpidament. A causa de la varietat de problemes, alguns
es poden dirigir a alumnat de primer de batxillerat, d'acord amb el criteri
del professor.
Metodologia
- La metodologia que cal seguir ha d'estar orientada a una primera introducció
teòrica dels conceptes, seguida d'alguna aplicació a tall d'exemple
i, finalment, a la resolució, per part de l'alumnat, dels problemes
que es plantegen. És interessant comparar els resultats numèrics
dels exemples i problemes amb d'altres que estan més a l'abast de la
ment humana, de manera que la visualització sigui més completa.
Orientacions tècniques
- La física d'acceleradors així com la física de partícules,
s'entenen molt millor amb recursos animats, que són recomanables d'alternar
amb les explicacions purament teòriques. En tot moment l'alumne ha
de veure que al darrere de tots aquests conceptes hi ha un grup de persones,
com ells, que hi treballen cada dia.

 
Full de l’alumnat
Objectiu
Estudiar i comprendre alguns dels conceptes relacionats amb els grans acceleradors
de partícules. Al final, l'alumne ha de ser capaç de relacionar
tots aquells conceptes que ha estudiat a classe amb la complexitat d'un accelerador.
Introducció
El Large Hadron Collider (LHC) o Gran Col•lisionador
d'Hadrons és un accelerador de partícules de 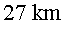 de circumferència situat a Ginebra, Suïssa, que fa col•lisionar
protons o ions pesants en quatre punts concrets. En aquests punts es troben
instal•lats detectors enormes que, com si d'una càmera fotogràfica
es tractés, enregistren totes les reacciones que tenen lloc al punt d'interacció.
Per dur a terme d'una manera efectiva les col•lisions, la intervenció
i coordinació de molts i diversos àmbits han de convergir en un
únic punt. Entre aquests camps es troben des de la dinàmica de
les partícules que circulen per l'accelerador fins a la superconductivitat
necessària per mantenir l'alt camp magnètic dels imants. Tot i
que la física que es troba al darrere pot ser d'un nivell alt, mitjançant
conceptes senzills i algunes simplificacions es pot arribar a comprendre el
funcionament bàsic dels acceleradors mitjançant els exemples i
problemes que aquí proposem.
de circumferència situat a Ginebra, Suïssa, que fa col•lisionar
protons o ions pesants en quatre punts concrets. En aquests punts es troben
instal•lats detectors enormes que, com si d'una càmera fotogràfica
es tractés, enregistren totes les reacciones que tenen lloc al punt d'interacció.
Per dur a terme d'una manera efectiva les col•lisions, la intervenció
i coordinació de molts i diversos àmbits han de convergir en un
únic punt. Entre aquests camps es troben des de la dinàmica de
les partícules que circulen per l'accelerador fins a la superconductivitat
necessària per mantenir l'alt camp magnètic dels imants. Tot i
que la física que es troba al darrere pot ser d'un nivell alt, mitjançant
conceptes senzills i algunes simplificacions es pot arribar a comprendre el
funcionament bàsic dels acceleradors mitjançant els exemples i
problemes que aquí proposem.
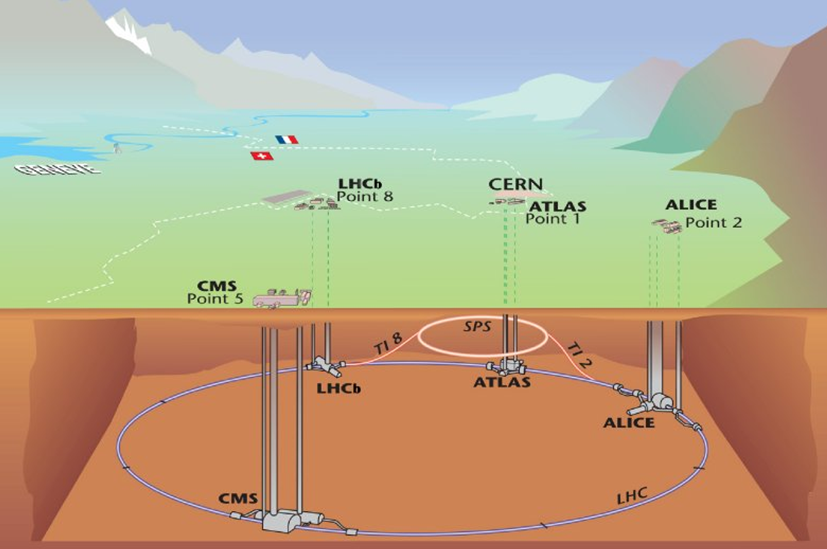 |
| Fig. 1: Esquema de l'LHC i els quatre detectors |
L'estructura bàsica del l'LHC consisteix en el que es coneix com 8
octants, 8 seccions clarament
diferenciades en què podem
dividir els 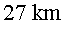 . A la
figura 2 es pot observar a què està dedicat cada octant. . A la
figura 2 es pot observar a què està dedicat cada octant.
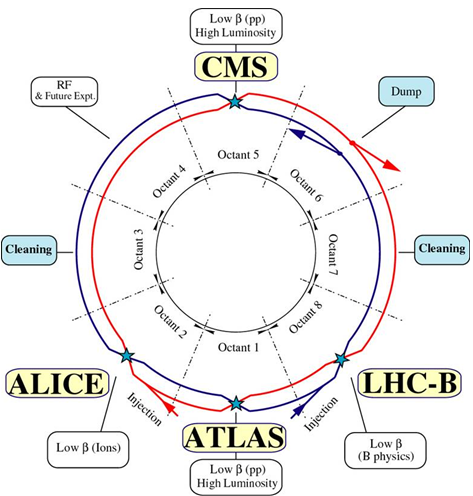 |
| Fig. 2: Els octans del LHC |
Per exemple, els octants 1,
2, 5 i 8 estan dedicats als experiments ATLAS, ALICE, CMS i LHCb, respectivament,
on els feixos de protons col•lisionen. A l'octant número 4
es troben les cavitats de radiofreqüència (RF), que proporcionen
el camp elèctric necessari per accelerar les partícules fins a
l'energia òptima de col•lisió. Els octants 3
i 7 allotgen els
anomenats col•limadors, instruments que permeten “netejar”
el núvol de partícules que envolta el feix principal. Finalment,
l'octant número 6
és l'anomenat dump, el lloc on van a parar els feixos de partícules
que han vist reduïda la seva càrrega de manera que ja no són
efectius. Per fer la forma d'anell que s'observa, són necessaris imants
que guiïn els protons o nuclis pesants al llarg dels 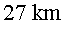 . .
Material
Cinemàtica i dinàmica
A manera d'escalfament, podem començar amb uns càlculs
senzills relacionats amb la cinemàtica dels acceleradors.
Considerem que la velocitat a què circulen els protons
per l'accelerador és igual a la velocitat de la llum (més endavant
veurem per què podem fer aquesta aproximació).
 P1.1) Calculeu
el nombre de voltes que fa cada protó per segon a l'LHC i quant triga
en fer una volta. P1.1) Calculeu
el nombre de voltes que fa cada protó per segon a l'LHC i quant triga
en fer una volta.
Sabem que es triguen uns 20
minuts a assolir l'energia necessària per realitzar les col•lisions
i assumim que la velocitat no varia (més endavant veurem també
què vol dir accelerar però mantenir la velocitat constant).
 P1.2) Calculeu
la distància total recorreguda i doneu una escala comparable per
visualitzar millor el resultat. P1.2) Calculeu
la distància total recorreguda i doneu una escala comparable per
visualitzar millor el resultat.
Els protons estan sotmesos constantment a la força centrípeta,
la causa del seu recorregut circular.
 P1.3) Calculeu
l'acceleració centrípeta que experimenten els protons i compareu-la
amb l'acceleració de la gravetat. Cal tenir en compte l'efecte de
la força de la gravetat, o en altres termes, els protons cauen verticalment?
Quantifiqueu aquest efecte. P1.3) Calculeu
l'acceleració centrípeta que experimenten els protons i compareu-la
amb l'acceleració de la gravetat. Cal tenir en compte l'efecte de
la força de la gravetat, o en altres termes, els protons cauen verticalment?
Quantifiqueu aquest efecte.
Moment i energia
El moment d'una partícula és una magnitud vectorial donada pel
producte de la seva massa i la velocitat que porta.
Per conveniència, moltes vegades fem un canvi de coordenades i expressem
el moment en el que anomenem coordenades esfèriques en tres
dimensions o polars en dues dimensions. D'aquesta manera podem escriure
el moment centrat en el punt on té lloc la col•lisió com:
Com l'energia, el moment és una magnitud que es conserva i, considerant
que les col•lisions tenen lloc a causa del xoc de dos feixos en direccions
oposades, el moment total de les partícules resultants ha de ser zero.
 P 2.1) Hi
ha partícules que no deixen rastre al detector, com per exemple els
neutrins, de manera que no s'en pot mesurar el moment directament. Com creieu
que s'en pot mesurar llavors el moment/energia? P 2.1) Hi
ha partícules que no deixen rastre al detector, com per exemple els
neutrins, de manera que no s'en pot mesurar el moment directament. Com creieu
que s'en pot mesurar llavors el moment/energia?
 P 2.2) Calculeu
a partir de l'expressió de l'energia cinètica no relativista
i sabent qu els protons són a P 2.2) Calculeu
a partir de l'expressió de l'energia cinètica no relativista
i sabent qu els protons són a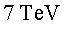 (unitat d'energia
(unitat d'energia 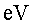 =electró-volt
, =electró-volt
, 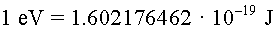 ) la velocitat
que haurien de tenir els protons. Us sembla estrany el resultat? ) la velocitat
que haurien de tenir els protons. Us sembla estrany el resultat?
Relativitat
Quan la velocitat de les partícules, els protons en el cas de l'LHC,
s'aproxima a la velocitat de la llum (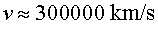 ),
comencen a aparèixer efectes que no es troben presents a velocitats més
baixes o no relativistes. D'aquesta manera, conceptes com el d'energia cinètica
són alterats i prenen una expressió diferent a la coneguda. Aquesta
és: ),
comencen a aparèixer efectes que no es troben presents a velocitats més
baixes o no relativistes. D'aquesta manera, conceptes com el d'energia cinètica
són alterats i prenen una expressió diferent a la coneguda. Aquesta
és:
on 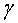 és el factor
relativista, s’expressa de la manera següent: és el factor
relativista, s’expressa de la manera següent:
 P3.1) Calculeu
el factor relativista P3.1) Calculeu
el factor relativista 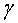 i la velocitat per a un protó de l'LHC amb una energia de
i la velocitat per a un protó de l'LHC amb una energia de 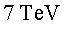 . .
 P3.2) Dibuixeu
una gràfica de la velocitat en funció de l'energia dels protons
i determineu el valor al qual tendeix assimptòticament la velocitat. P3.2) Dibuixeu
una gràfica de la velocitat en funció de l'energia dels protons
i determineu el valor al qual tendeix assimptòticament la velocitat.
Buit i equació dels gasos ideals.
El buit en un accelerador és fonamental per evitar col•lisions
paràsites de les partícules que componen el feix amb les partícules
que romanen a l'accelerador i fan que d'aquesta manera el feix es degradi ràpidament
i a la vegada generi radiacions de fons que poden arribar a apantallar les pròpies
col•lisions. A la canonada per on passa el feix, la pressió és
d'aproximadament 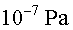 a
una temperatura d'uns a
una temperatura d'uns 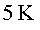 i a prop de
i a prop de 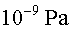 a prop
dels punts de col•lisió. Aquesta pressió és al voltant
de 100 vegades més
petita que a la superfície de la Lluna. a prop
dels punts de col•lisió. Aquesta pressió és al voltant
de 100 vegades més
petita que a la superfície de la Lluna.
 P4.1) Calculeu
el volum que ocupa el tub per on passa el feix assumint que té un
radi d'uns 3 cm
i que es pot considerar igual arreu de tota la circumferència. Aquest
volum, amb què es comparable en termes quotidians? P4.1) Calculeu
el volum que ocupa el tub per on passa el feix assumint que té un
radi d'uns 3 cm
i que es pot considerar igual arreu de tota la circumferència. Aquest
volum, amb què es comparable en termes quotidians?
La densitat del gas residual pot variar pel fet que les fonts
de gas, principalment els electrons i els que són induïts pels fotons,
depèn de les propietats de la superfície i de com funcioni la
màquina.
Per exemple, la desorció induïda pels ions és el resultat
de la col•lisió dels protons amb molècules residuals, que
genera partícules carregades amb una relació càrrega/massa
que no els permet portar la trajectòria correcta i per això col•lisionen
amb les parets del tub i alliberen gasos. Els electrons creats en aquestes col•lisions
protó-molècula i els fotons emesos per radiació de sincrotró
també produeixen desorció gasosa. Els principals gasos emesos
són 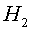 , , 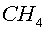 , ,
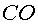 , , 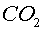 , ,
 i gasos nobles. Per
adonar-nos de la importància de la necessitat d'un buit tan gran podem
estimar el nombre de molècules per metre cúbic a dins del tub. i gasos nobles. Per
adonar-nos de la importància de la necessitat d'un buit tan gran podem
estimar el nombre de molècules per metre cúbic a dins del tub.
 P4.2) Utilitzant
l'equació dels gasos ideals ( P4.2) Utilitzant
l'equació dels gasos ideals (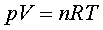 ),
estimeu el nombre de molècules de gas que hi ha al tub de l'LHC a
temperatura ambient i amb una pressió d' ),
estimeu el nombre de molècules de gas que hi ha al tub de l'LHC a
temperatura ambient i amb una pressió d'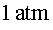 (atm=
atmosfera) i un cop s'ha refredat a una temperatura de (atm=
atmosfera) i un cop s'ha refredat a una temperatura de 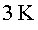 i s'hi ha fet el buit.
i s'hi ha fet el buit.
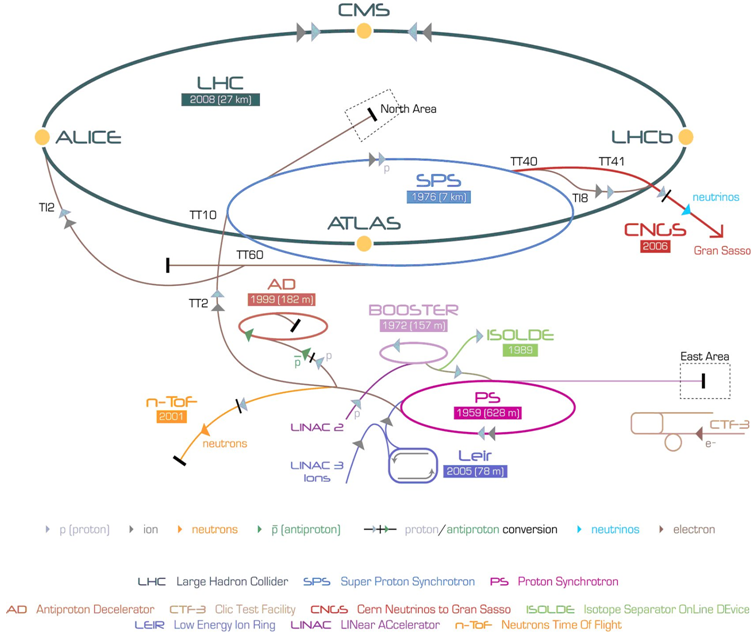 |
| Fig. 3: Esquema del conjunt d'acceleradors intercomunicats del
CERN |
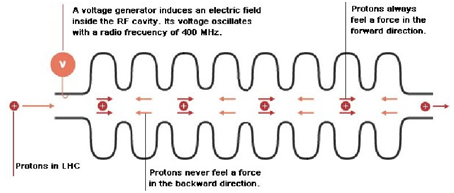 |
| Fig. 4: Esquema del funcionament d'una cavitat de radiofreqüència |
Electricitat
A l'LHC i la seva cadena d'injecció els protons són
accelerats des de l'estat de quasi repòs fins a la seva energia final
( ). Aquesta acceleració
es duu a terme mitjançant camps elèctrics que volta rere volta
van imprimint una mica més d'energia a les partícules que hi passen.
Els dispositius encarregats de generar aquest camp elèctric són
les anomenades cavitats de radiofreqüència. Les cavitats
de radiofreqüència generen una ona de camp elèctric sincronitzada
amb el pas del feix de protons (d'aquí que anomenem sincrotró
a aquest tipus d'acceleradors) de manera que a cada volta experimenten un increment
de l'energia. ). Aquesta acceleració
es duu a terme mitjançant camps elèctrics que volta rere volta
van imprimint una mica més d'energia a les partícules que hi passen.
Els dispositius encarregats de generar aquest camp elèctric són
les anomenades cavitats de radiofreqüència. Les cavitats
de radiofreqüència generen una ona de camp elèctric sincronitzada
amb el pas del feix de protons (d'aquí que anomenem sincrotró
a aquest tipus d'acceleradors) de manera que a cada volta experimenten un increment
de l'energia.
 P5.1) L'energia
a què s'injecten protons a l'LHC és P5.1) L'energia
a què s'injecten protons a l'LHC és 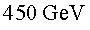 .
Calculeu quantes voltes necessiten els protons per assolir la seva energia
nominal ( .
Calculeu quantes voltes necessiten els protons per assolir la seva energia
nominal (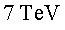 ) si les
cavitats de radiofreqüència generen un potencial elèctric
de ) si les
cavitats de radiofreqüència generen un potencial elèctric
de 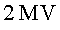 i hi ha un total
de 8 cavitats
instal•lades a l'LHC. Quant de temps es requereix per dur a terme
l'acceleració completa? i hi ha un total
de 8 cavitats
instal•lades a l'LHC. Quant de temps es requereix per dur a terme
l'acceleració completa?
 P5.2) El temps
total en la vida real és d'uns 20
minuts. Per què creieu que hi ha tanta diferència entre el
temps calculat i el temps real? P5.2) El temps
total en la vida real és d'uns 20
minuts. Per què creieu que hi ha tanta diferència entre el
temps calculat i el temps real?
 |
| Fig. 5: Cavitat de radiofreqüència. |
Magnetisme
Els protons han de seguir una trajectòria circular
marcada per l'anell de 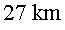 de llargada. Per això s'utilitza un camp magnètic extremadament
potent que guia les partícules al llarg de l'anell i permet que les col•lisions
tinguin lloc de manera controlada. Seguint l'equació de Lorentz, una
partícula amb càrrega
de llargada. Per això s'utilitza un camp magnètic extremadament
potent que guia les partícules al llarg de l'anell i permet que les col•lisions
tinguin lloc de manera controlada. Seguint l'equació de Lorentz, una
partícula amb càrrega 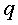 i velocitat
i velocitat  quan entra
en un camp magnètic quan entra
en un camp magnètic 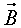 experimenta una força expressada de la manera següent:
experimenta una força expressada de la manera següent:
Es pot veure que la força és el producte vectorial del vector
velocitat i del vector camp magnètic. D'aquesta manera s'obté
la força, també una magnitud vectorial. Seguint la regla de la
mà dreta, podem esbrinar quina direcció ha de tenir el camp magnètic
per tal de corbar les partícules radialment. Aquesta direcció,
tal com es veu a la figura 6, ha de ser vertical, positiva o negativa depenent
del sentit de gir dels protons.
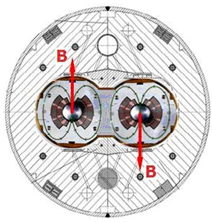 |
| Fig. 6: |
 P6.1)
Sabent que la força que ha de fer l'imant sobre els protons ha de
ser la força per mantenir-los units en la trajectòria circular
(centrípeta), calculeu el camp magnètic dels imants superconductors
de l'LHC. Compareu aquest resultat amb els camps magnètics de la
Terra i de l'imant d'un dispositiu de ressonància magnètica. P6.1)
Sabent que la força que ha de fer l'imant sobre els protons ha de
ser la força per mantenir-los units en la trajectòria circular
(centrípeta), calculeu el camp magnètic dels imants superconductors
de l'LHC. Compareu aquest resultat amb els camps magnètics de la
Terra i de l'imant d'un dispositiu de ressonància magnètica.
 P6.2) El camp
magnètic necessari es crea mitjançant inducció magnètica,
fent passar un corrent molt intens per uns cables, el qual, d'acord amb
la llei de Biot-Savart, crea un camp magnètic a l'espai per on circulen
els protons. Quin és el corrent necessari per generar el camp magnètic
calculat a l'apartat anterior? P6.2) El camp
magnètic necessari es crea mitjançant inducció magnètica,
fent passar un corrent molt intens per uns cables, el qual, d'acord amb
la llei de Biot-Savart, crea un camp magnètic a l'espai per on circulen
els protons. Quin és el corrent necessari per generar el camp magnètic
calculat a l'apartat anterior?
Com haureu pogut observar, els camps magnètics necessaris són
extremadament alts, impossibles d'aconseguir amb imants permanents o amb electroimants
convencionals.
 P7.1)
Busqueu què vol dir el concepte de superconductivitat i
expliqueu per què és necessita que l'LHC estigui refrigerat
a uns P7.1)
Busqueu què vol dir el concepte de superconductivitat i
expliqueu per què és necessita que l'LHC estigui refrigerat
a uns 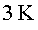 constantment.
Quines aplicacions de la superconductivitat en un futur trobeu que poden
ser interessants? constantment.
Quines aplicacions de la superconductivitat en un futur trobeu que poden
ser interessants?
Lluminositat i secció eficaç
La lluminositat és un dels paràmetres més importants d'un
col•lisionador ja que dóna una idea del nombre de col•lisions
que s'hi produeixen cada segon. És per això que, a priori, volem
que aquest nombre sigui el més gran possible. Per entendre millor el
concepte de lluminositat necessitem introduir el concepte de secció
eficaç. La secció eficaç d'un procés qualsevol
ens indica la probabilitat que aquest es produeixi en una col•lisió
a una energia determinada. Successos molt estranys, com poden ser l'aparició
d'un bosó de Higgs o de noves partícules encara no descobertes,
tindran una secció eficaç de producció molt petita. Podem
llavors relacionar ambdues quantitats i definir-ne una de nova:
on 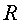 ens indica el nombre de successos amb secció eficaç
ens indica el nombre de successos amb secció eficaç 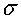 que
hem tingut amb una lluminositat que
hem tingut amb una lluminositat 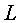 .
Si anem enregistrant la lluminositat que tenim en cada moment i l'anem sumant
al llarg del temps, tenim el que coneixem com a lluminositat integrada.
En la figura 8 es mostra la lluminositat integrada enregistrada per l'experiment
CMS durant els primers anys de funcionament de l'LHC. .
Si anem enregistrant la lluminositat que tenim en cada moment i l'anem sumant
al llarg del temps, tenim el que coneixem com a lluminositat integrada.
En la figura 8 es mostra la lluminositat integrada enregistrada per l'experiment
CMS durant els primers anys de funcionament de l'LHC.
 |
| Fig. 8: Lluminositat integrada enregistrada pel CMS |
 P8.1) Expliqueu
amb les vostres paraules les conclusions que podeu treure d'aquesta gràfica. P8.1) Expliqueu
amb les vostres paraules les conclusions que podeu treure d'aquesta gràfica.
 P8.2) Quina
era la lluminositat integrada al CMS el dia del descobriment del bosó
de Higgs? P8.2) Quina
era la lluminositat integrada al CMS el dia del descobriment del bosó
de Higgs?
Temps de vida del feix
Malgrat la gran població de protons que hi ha al feix (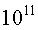 protons) i que només una vintena d'aquests es perden cada vegada que
aquests feixos es creuen, a causa de la gran freqüència de revolució,
el nombre de baixes pot ser considerable de tal manera que al cap d'una estona
la lluminositat pot ser tan baixa que els feixos esdevinguin inservibles. Quan
això passa, s'extreu el feix “gastat” i se n'injecta un de
nou. El temps que passa entre la injecció i l'extracció del feix
és el que anomenem temps de vida.
protons) i que només una vintena d'aquests es perden cada vegada que
aquests feixos es creuen, a causa de la gran freqüència de revolució,
el nombre de baixes pot ser considerable de tal manera que al cap d'una estona
la lluminositat pot ser tan baixa que els feixos esdevinguin inservibles. Quan
això passa, s'extreu el feix “gastat” i se n'injecta un de
nou. El temps que passa entre la injecció i l'extracció del feix
és el que anomenem temps de vida.
 P9.1) Si considereu
que el feix de protons està compost per aproximadament P9.1) Si considereu
que el feix de protons està compost per aproximadament 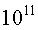 partícules i que per cada xoc de feixos es perden 20
protons i que tenim 4
punts d'interacció, calculeu el nombre de voltes en què
la intensitat del feix es redueix un factor 10
i estimeu el temps de vida del feix en aquest cas.
partícules i que per cada xoc de feixos es perden 20
protons i que tenim 4
punts d'interacció, calculeu el nombre de voltes en què
la intensitat del feix es redueix un factor 10
i estimeu el temps de vida del feix en aquest cas.
 P9.2) Quines
altres fonts creieu vosaltres que existeixen que fan reduir el nombre de
protons als feixos? P9.2) Quines
altres fonts creieu vosaltres que existeixen que fan reduir el nombre de
protons als feixos?
 |
| Fig. 9: Sincrotró Alba. |
Radiació de sincrotró
Un efecte notable d'accelerar partícules carregades
és que aquestes emeten un tipus concret de radiació que anomenem
radiació de sincrotró. Aquesta radiació fa que
les partícules perdin certa energia en cada volta, de manera que aquesta
requereix una acceleració constant; en cada volta s'ha de tornar a donar
l'energia perduda per mantenir l'energia als punts de col•lisió
constant.
L'expressió que dóna la potència perduda per volta és:
on 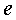 és la càrrega
de l'electró, és la càrrega
de l'electró, 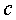 la velocitat de la llum,
la velocitat de la llum, 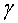 el factor relativista,
el factor relativista, 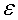 la constant dielèctrica i
la constant dielèctrica i 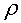 el radi de curvatura.
el radi de curvatura.
 P10.1)
Calculeu l'energia perduda en cada volta al Gran Col•lisionador Electró-Positró
(LEP, Large Electron-Positron Collider) i a l'LHC. Quina conclusió
en podeu treure? Quin efecte pot tenir aquest resultat en el disseny i construcció
dels futurs col•lisionadors que haurien de funcionar amb una energia
més alta? P10.1)
Calculeu l'energia perduda en cada volta al Gran Col•lisionador Electró-Positró
(LEP, Large Electron-Positron Collider) i a l'LHC. Quina conclusió
en podeu treure? Quin efecte pot tenir aquest resultat en el disseny i construcció
dels futurs col•lisionadors que haurien de funcionar amb una energia
més alta?
Però no sempre aquesta radiació és perjudicial
per al propòsit de l'accelerador. De fet, existeixen el que es coneix
com a fonts de llum de sincrotró com ara la construïda
i posada en funcionament fa molt poc a Cerdanyola del Vallès: el sincrotró
Alba. Aquest tipus d'instal•lacions utilitzen la radiació emesa
pels electrons que hi circulen com a microscopi molt potent. Emprant aquesta
tècnica, es poden observar amb molt de detall l'estructura de les proteïnes
i la composició de certs materials.
Extra: Produïm el Higgs
El bosó de Higgs és una de les principals motivacions
de l'LHC i dels seus experiments. És una partícula difícil
de produir, és a dir, la probabilitat de generar un bosó de Higgs
a l'LHC és molt petita. A la gràfica següent es mostren les
diferents maneres
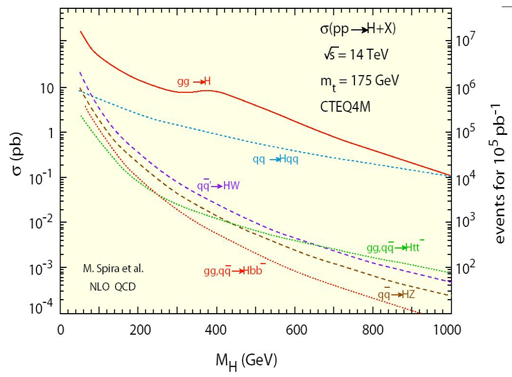 |
| Fig. 10 |
en què es pot produir un Higgs, sempre acompanyat per
alguna altra partícula. Les diferents línies puntejades representen
les diferents reaccions que donen lloc a un bosó de Higgs. Per exemple,
la línia de color cian, representa la probabilitat de produir el Higgs
a partir de dos quarks i que aquest vagi acompanyat de dos quarks més,
en funció de la massa del bosó de Higgs, que avui ja sabem que
és d'uns 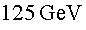 . La
línia vermella representa la suma total de les probabilitats que dos
gluons (portadors de la força nuclear forta i que es troben a dins del
protó) donin lloc a un Higgs en qualsevol dels modes que es mostren.
Aquesta probabilitat s'anomena secció eficaç i s’expressa
en picobarns ( . La
línia vermella representa la suma total de les probabilitats que dos
gluons (portadors de la força nuclear forta i que es troben a dins del
protó) donin lloc a un Higgs en qualsevol dels modes que es mostren.
Aquesta probabilitat s'anomena secció eficaç i s’expressa
en picobarns (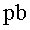 ), que
equivalen a ), que
equivalen a 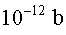 , ( el barn
( , ( el barn
( ) és una unitat
de superfície: ) és una unitat
de superfície: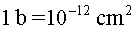 ). ).
 P11.1) Busqueu
la definició de la unitat de secció eficaç, barn, i
relacioneu el concepte de secció eficaç amb el concepte
de lluminositat. P11.1) Busqueu
la definició de la unitat de secció eficaç, barn, i
relacioneu el concepte de secció eficaç amb el concepte
de lluminositat.
 P11.2) Per
què penseu que la probabilitat baixa a mesura que la massa del bosó
de Higgs augmenta? P11.2) Per
què penseu que la probabilitat baixa a mesura que la massa del bosó
de Higgs augmenta?
 P11.3) Suposant
que el bosó de Higgs té una massa d'uns P11.3) Suposant
que el bosó de Higgs té una massa d'uns 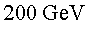 ,
estimeu la quantitat de bosons de Higgs que es produirien després
de d'1 any produint
col•lisions a ,
estimeu la quantitat de bosons de Higgs que es produirien després
de d'1 any produint
col•lisions a  amb una lluminositat instantània de
amb una lluminositat instantània de 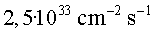 . .
 |
| Fig. 11 |
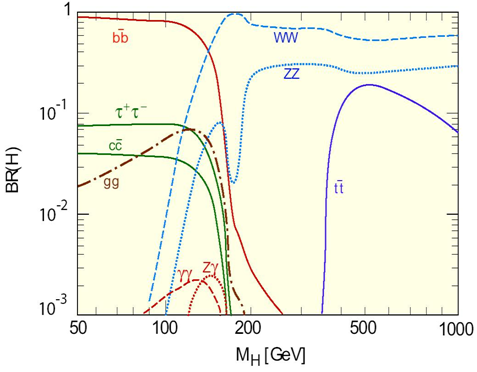
En realitat, el bosó de Higgs no es detecta directament
sinó que el que es detecta són les partícules en què
es desintegra. Hi ha diferents maneres en què els bosons de Higgs es
poden desintegrar a partir de la col•lisió entre protons. Cadascuna
d'aquestes maneres s'anomena canal. Però no tots els canals
són igual de probables, hi ha canals que són més probables
que d'altres. Per exemple, és més probable que el bosó
de Higgs es desintegri en dos bosons 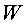 (portadors de la força electrofeble) que en dos fotons (portadors de
la força electromagnètica). En la següent figura es mostren
les diferents probabilitats (branching rations,
(portadors de la força electrofeble) que en dos fotons (portadors de
la força electromagnètica). En la següent figura es mostren
les diferents probabilitats (branching rations, 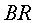 )
del bosó de Higgs en funció de la seva massa. )
del bosó de Higgs en funció de la seva massa.
 P11.4) Suposant
que la massa del bosó de Higgs fos superior a P11.4) Suposant
que la massa del bosó de Higgs fos superior a 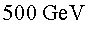 ,
quins són els canals en què es pot desintegrar? Vol dir això
que és impossible que es desintegri en qualsevol altre canal? ,
quins són els canals en què es pot desintegrar? Vol dir això
que és impossible que es desintegri en qualsevol altre canal?
 P11.5) Estimeu
a partir de la figura 9 i del resultat de la pregunta P11.4
el nombre de parells P11.5) Estimeu
a partir de la figura 9 i del resultat de la pregunta P11.4
el nombre de parells 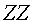 que es van produir durant aquest període. Creieu que és un
nombre suficientment alt com per treure una bona estadística?
que es van produir durant aquest període. Creieu que és un
nombre suficientment alt com per treure una bona estadística?

 
Solucions
 P1.1) Calculeu
el nombre de voltes que fa a l'LHC cada protó per segon i quant triga
a fer una volta. P1.1) Calculeu
el nombre de voltes que fa a l'LHC cada protó per segon i quant triga
a fer una volta.

 P1.2) Calculeu
la distància total recorreguda i doneu una escala comparable per
visualitzar millor el resultat. P1.2) Calculeu
la distància total recorreguda i doneu una escala comparable per
visualitzar millor el resultat.
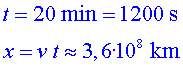
Els protons viatgen una distància equivalent
a anar de la Terra al Sol i tornar i tornar a anar-hi mig camí.
 P1.3) Calculeu
l'acceleració centrípeta que experimenten els protons i compareu-la
amb l'acceleració de la gravetat. Cal tenir en compte l'efecte de
la força de la gravetat, o, en altres termes, els protons cauen verticalment?
Quantifiqueu aquest efecte. P1.3) Calculeu
l'acceleració centrípeta que experimenten els protons i compareu-la
amb l'acceleració de la gravetat. Cal tenir en compte l'efecte de
la força de la gravetat, o, en altres termes, els protons cauen verticalment?
Quantifiqueu aquest efecte.
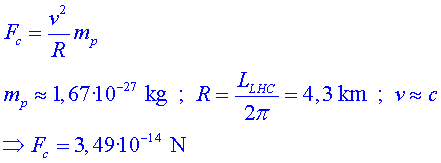
Mentre que la força de la gravetat és
12 ordres de magnitud més petita.
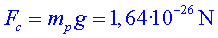
Atenció, el càlcul de la força centrípeta és
erroni, ja que no s'han considerat correccions relativistes. Aquest resultat
pot portar a càlculs posteriorment. Es convida l'alumne a refer el
càlcul quan s'hi han introduït els conceptes de relativitat
especial i factor relativista. Fem aquí un resum (per
al professorat) del raonament per trobar la força centrípeta
relativista. Suposem que el moviment és circular uniforme i té
un radi 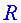 . Tindrem . Tindrem
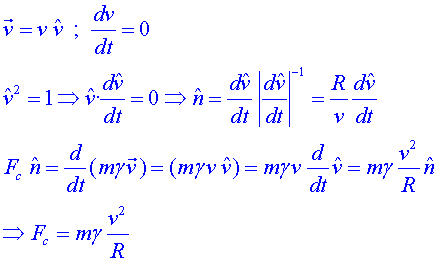
El resultat numèric en aquest cas seria:

on és el factor
relativista introduït en la propera secció. Aquest és
el resultat que s'ha d'utilitzar per calcular el camp magnètic dels
imans. és el factor
relativista introduït en la propera secció. Aquest és
el resultat que s'ha d'utilitzar per calcular el camp magnètic dels
imans.
Una altra aproximació que hem utilitzat ha estat pensar que e l'LHC
és un anell perfecte, però en realitat està compost
per 8 seccions corbes i 8 de rectes que fan que el radi efectiu de la màquina
sigui més gran del que en realitat representen la curvatura dels
imans. La forçaa centrípeta que experimenten els protons és
més correctament d'uns 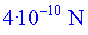 .
Es recomana que els alumnes facin la comparativa entre amdós resultats. .
Es recomana que els alumnes facin la comparativa entre amdós resultats.
 P 2.1) Hi
ha partícules que no deixen rastre al detector, com per exemple els
neutrins, de manera que no s'en pot mesurar el moment directament. Com creieu
que s'en pot mesurar llavors el moment/energia? P 2.1) Hi
ha partícules que no deixen rastre al detector, com per exemple els
neutrins, de manera que no s'en pot mesurar el moment directament. Com creieu
que s'en pot mesurar llavors el moment/energia?
Mitjançant la llei de la conservació
de l'energia. Sabem quina energia imprimim a la col·lisió
( ) i podem mesurar
tota l'nergia dels productes amb el nostre detector. Quan fem la diferència
de les energies, si hi ha un defecte d'energia en els productes significa
que és l'energia dels neutrins o altres partícules que no
han interaccionat amb el detector. La llei de conservació del moment,
a més, ens permet trobar les direccions en les quals han sortit aqueslles
partícules "fantasma". ) i podem mesurar
tota l'nergia dels productes amb el nostre detector. Quan fem la diferència
de les energies, si hi ha un defecte d'energia en els productes significa
que és l'energia dels neutrins o altres partícules que no
han interaccionat amb el detector. La llei de conservació del moment,
a més, ens permet trobar les direccions en les quals han sortit aqueslles
partícules "fantasma".
 P 2.2) Calculeu
a partir de l'expressió de l'energia cinètica no relativista
i sabent qu els protons són a P 2.2) Calculeu
a partir de l'expressió de l'energia cinètica no relativista
i sabent qu els protons són a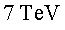 ,
(unitat d'energia ,
(unitat d'energia 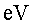 =electró-volt
, =electró-volt
, 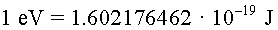 ) la velocitat
que haurien de tenir els protons. Us sembla estrany el resultat? ) la velocitat
que haurien de tenir els protons. Us sembla estrany el resultat?
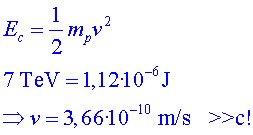
 P3.1) Calculeu
el factor relativista P3.1) Calculeu
el factor relativista 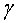 i la velocitat per a un protó de l'LHC amb una energia de
i la velocitat per a un protó de l'LHC amb una energia de 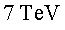 . .
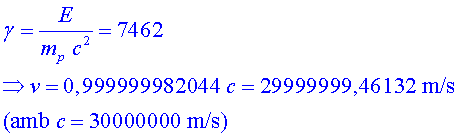
 P3.2) Dibuixeu
una gràfica de la velocitat en funció de l'energia dels protons
i determineu el valor al qual tendeix asimptòticament la velocitat. P3.2) Dibuixeu
una gràfica de la velocitat en funció de l'energia dels protons
i determineu el valor al qual tendeix asimptòticament la velocitat.
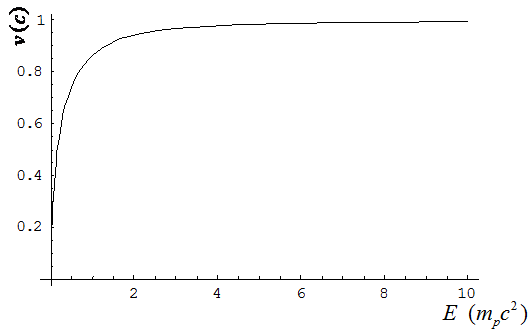 |
| Fig. 12: Com es pot apreciar a la figura,
l'energia creix assimptòticament quan la velocitat s'apropa
a la velocitat de la llum. El que estableix aquesta gràfica
és el fet de que les partícules no poden superar la
velocitat de la llum o que es requereix una energia infinita per arribar-hi. |
Buit i equació dels gasos ideals.
El buit en un accelerador és fonamental per evitar col•lisions
paràsites de les partícules que composen el feix amb les partícules
que romanen a l'accelerador i fan que d'aquesta manera el feix es degradi ràpidament
i a la vegada generi radiacions de fons que poden arribar a apantallar les col•lisions.
A la canonada por on passa el feix, la pressió és d'aproximadament
 a una temperatura d'uns a una temperatura d'uns
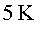 i a prop de i a prop de 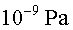 a prop dels punts de col•lisió. Aquesta pressió és
al voltant de 100
vegades més petita que a la superfície de la Lluna.
a prop dels punts de col•lisió. Aquesta pressió és
al voltant de 100
vegades més petita que a la superfície de la Lluna.
 P 4.1) Calculeu
el volum que ocupa el tub per on passa el feix assumint que té un
radi d'uns 3 cm
i que es pot considerar igual arreu de tota la circumferència. Aquest
volum, amb què es comparable en termes quotidians? P 4.1) Calculeu
el volum que ocupa el tub per on passa el feix assumint que té un
radi d'uns 3 cm
i que es pot considerar igual arreu de tota la circumferència. Aquest
volum, amb què es comparable en termes quotidians?
Aproximacó, cilindre: es pot considerar
que el tub del LHC és un cilindre ja que el radi de curvatura
és molt gran. En aquest cas,
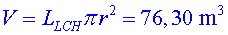
Aquest volum és comparable a una habitació
d'uns 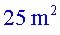 , com
l'aula on són asseguts. Llavors, buidar l'LHC és com buidar
tota la classe fins que gairabé no quedi cap molècula
d'aire. , com
l'aula on són asseguts. Llavors, buidar l'LHC és com buidar
tota la classe fins que gairabé no quedi cap molècula
d'aire.
La densitat del gas residual, que pot variar per les fonts
de gas, principalment els electrons i els que són induïts pels fotons,
depèn de les propietats de la superfície i de com funcioni la
màquina.
Per exemple, la desorció induïda pels ions és el resultat
de la col•lisió dels protons amb molècules residuals, que
genera partícules carregades amb una relació càrrega/massa
que no els permet portar la trajectòria correcta i per això col•lisionen
amb les parets del tub i alliberen gasos. Els electrons creats en aquestes col•lisions
protó-molècula i els fotons emesos per radiació de sincrotró
també produeixen desorció gasosa. Els principals gasos emesos
són 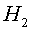 , ,  , ,
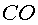 , , 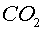 , ,
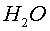 i gasos nobles. Per
adonar-nos de la importància de la necessitat d'un buit tan gran podem
estimar el nombre de molècules per metre cúbic a dins del tub. i gasos nobles. Per
adonar-nos de la importància de la necessitat d'un buit tan gran podem
estimar el nombre de molècules per metre cúbic a dins del tub.
 P.4.2) Utilitzant
l'equació dels gasos ideals ( P.4.2) Utilitzant
l'equació dels gasos ideals (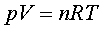 ),
estimeu el nombre de molècules de gas que hi ha al tub de l'LHC a
temperatura ambient i amb una pressió d' ),
estimeu el nombre de molècules de gas que hi ha al tub de l'LHC a
temperatura ambient i amb una pressió d' (atm=
atmosfera) i un cop s'ha refredat a una temperatura de (atm=
atmosfera) i un cop s'ha refredat a una temperatura de  s'hi ha fet el buit.
s'hi ha fet el buit.
Prenem una temperatura ambient de 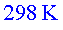 i
un buit de i
un buit de 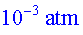 .
Obtenim .
Obtenim
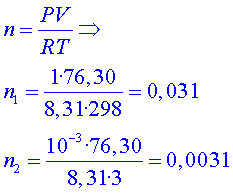
 P5.1)
L'energia a què s'injecten protons a l'LHC és P5.1)
L'energia a què s'injecten protons a l'LHC és 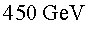 .
Calculeu quantes voltes necessiten els protons per assolir la seva energia
nominal ( .
Calculeu quantes voltes necessiten els protons per assolir la seva energia
nominal (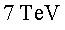 ) si les
cavitats de radiofreqüència generen un potencial elèctric
de ) si les
cavitats de radiofreqüència generen un potencial elèctric
de 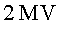 i hi ha un total
de 8 cavitats
instal•lades a l'LHC. Quant de temps es requereix per dur a terme
l'acceleració completa? i hi ha un total
de 8 cavitats
instal•lades a l'LHC. Quant de temps es requereix per dur a terme
l'acceleració completa?
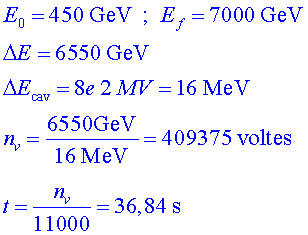
Recordem que un
protó dóna 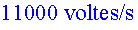 . .
 P5.2) El temps
total en la vida real és d'uns 20
minuts. Per què creieu que hi ha tanta diferència entre el
temps calculat i el temps real? P5.2) El temps
total en la vida real és d'uns 20
minuts. Per què creieu que hi ha tanta diferència entre el
temps calculat i el temps real?
En el món
real, hi ha un factor d'eficiència que redueix l'energia que
es transmet al feix en cada volta i que depèn de diversos factors.
Aquest factor d'eficiència éss al voltant d'un 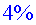 . .
 P6.1)
Sabent que la força que ha de fer l'imant sobre els protons ha de
ser la força per mantenir-los units en la trajectòria circular
(centrípeta), calculeu el camp magnètic dels imants superconductors
de l'LHC. Compareu aquest resultat amb els camps magnètics de la
Terra i de l'imant d'un dispositiu de ressonància magnètica. P6.1)
Sabent que la força que ha de fer l'imant sobre els protons ha de
ser la força per mantenir-los units en la trajectòria circular
(centrípeta), calculeu el camp magnètic dels imants superconductors
de l'LHC. Compareu aquest resultat amb els camps magnètics de la
Terra i de l'imant d'un dispositiu de ressonància magnètica.
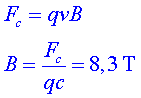
El camp magnètic a la superfície de la Terra pot variar
entre 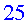 i i 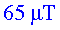 ,
unes ,
unes 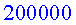 vegades
més dèbil que el camp magnètic dels dipols de l'LHC.
La majoria d'imants utilitzats en les ressonàncies magnètiques
són d'aproximadament vegades
més dèbil que el camp magnètic dels dipols de l'LHC.
La majoria d'imants utilitzats en les ressonàncies magnètiques
són d'aproximadament 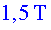 . .
 P6.2) El camp
magnètic necessari es crea mitjançant inducció magnètica,
fent passar un corrent molt intens per uns cables, el qual, d'acord amb
la llei de Biot-Savart, crea un camp magnètic a l'espai per on circulen
els protons. Quin és el corrent necessari per generar el camp magnètic
calculat a l'apartat anterior? P6.2) El camp
magnètic necessari es crea mitjançant inducció magnètica,
fent passar un corrent molt intens per uns cables, el qual, d'acord amb
la llei de Biot-Savart, crea un camp magnètic a l'espai per on circulen
els protons. Quin és el corrent necessari per generar el camp magnètic
calculat a l'apartat anterior?

 P7.1) Busqueu
què vol dir el concepte de superconductivitat i expliqueu
per què es necessita que l'LHC estigui refrigerat a uns P7.1) Busqueu
què vol dir el concepte de superconductivitat i expliqueu
per què es necessita que l'LHC estigui refrigerat a uns 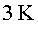 constantment. Quines aplicacions de la superconductivitat en un futur trobeu
que poden ser interessants?
constantment. Quines aplicacions de la superconductivitat en un futur trobeu
que poden ser interessants?
- Llei d'Ohm.
- Baixes temperatures.
- Ressistivitat.
- Transport d'energia.
 P8.1) Expliqueu
amb les vostres paraules les conclusions que podeu treure d'aquesta gràfica. P8.1) Expliqueu
amb les vostres paraules les conclusions que podeu treure d'aquesta gràfica.
- El LHC funciona molt bé.
- El segon any es va aconseguir una luminositat
més de 100
vegades més gran que el primer any i el darrer any es va aconseguir
multiplicar per 4 la luminositat integrada de l'any anterior.
- Hi ha períodes en què no s'acumula
luminositat. Aquests períodes són els de manteniment de
la màquina.
- El darrer any l'energia es va incrementar de
7 a 8
TeV.
 P8.2) Quina
era la lluminositat integrada al CMS el dia del descobriment del bosó
de Higgs? P8.2) Quina
era la lluminositat integrada al CMS el dia del descobriment del bosó
de Higgs?
La luminositat del 4 de Juliol de 2012 era d'aproximadament
7 femtobarns
inversos a 8 TeV
i uns 6 a 7
TeV de l'any anterior.
 P9.1) Si considereu
que el feix de protons està compost per aproximadament P9.1) Si considereu
que el feix de protons està compost per aproximadament  partícules i que per cada xoc de feixos es perden 20 protons i que
tenim 4 punts d'interacció, calculeu el nombre de voltes en què
la intensitat del feix es redueix un factor 10
i estimeu el temps de vida del feix en aquest cas.
partícules i que per cada xoc de feixos es perden 20 protons i que
tenim 4 punts d'interacció, calculeu el nombre de voltes en què
la intensitat del feix es redueix un factor 10
i estimeu el temps de vida del feix en aquest cas.
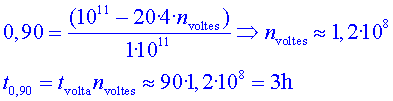
 P9.2) Quines
altres fonts creieu vosaltres que existeixen que fan reduir el nombre de
protons als feixos? P9.2) Quines
altres fonts creieu vosaltres que existeixen que fan reduir el nombre de
protons als feixos?
A part de les pèrdues
en les col·lisions també es produeixen pèrdues
al llarg dels 27
kilòmetres a causa dels sistemes de col·limació,
que "netegen" el feix de partícules que s'apropen massa
al tub i el poden fer malbé. També hi ha pèrdues
incontrolades per diferents motius, com ara col·lisions amb molècules
que romanen a la canonada per on passa el feix. Algunes partícules,
tot i no col·lisionar, són deflectides pels camps magnètics
que provoca el feix circulant en sentit oposat.
 P10.1) Calculeu
l'energia perduda per cada volta al Gran Col•lisionador Electró-Positró
(LEP, Large Electron-Positron Collider) i a l'LHC. Quina conclusió
en podeu treure? Quin efecte pot tenir aquest resultat en el disseny i construcció
dels futurs col•lisionadors que haurien de funcionar amb una energia
més alta? P10.1) Calculeu
l'energia perduda per cada volta al Gran Col•lisionador Electró-Positró
(LEP, Large Electron-Positron Collider) i a l'LHC. Quina conclusió
en podeu treure? Quin efecte pot tenir aquest resultat en el disseny i construcció
dels futurs col•lisionadors que haurien de funcionar amb una energia
més alta?
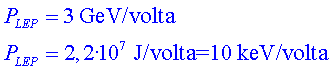
A causa
de la baixa massa dels electrons, aquests irradien molta més
energia, com es pot veure als càlculs, tot i que els protons
a l'LHC són molt més energètics. Això fa
que el futur dels acceleradors comporti haver de considerar col·lisionadors
lineals, que redueixen la radiació de sincrotró gairebé
a zero, o considerar acceleradors circulars molts grans. Actualment,
es consideren acceleradors lineals d'entre 30
i 50 km i
acceleradors circulars de 100
km.
 P11.1) Busqueu
la definició de la unitat de secció eficaç, barn,
i relacioneu el concepte de secció eficaç amb el
concepte de lluminositat. P11.1) Busqueu
la definició de la unitat de secció eficaç, barn,
i relacioneu el concepte de secció eficaç amb el
concepte de lluminositat.
 P11.2) Per
què penseu que la probabilitat baixa a mesura que la massa del bosó
de Higgs augmenta? P11.2) Per
què penseu que la probabilitat baixa a mesura que la massa del bosó
de Higgs augmenta?
Si produïm col·lisions amb una energia
fixada a mesura que la massa del Higgs és més gran, cada
cop és menys probable produir-la, ja que l'energia de la que
disposem cada cop és relativament més baixa.
 P11.3) Suposant
que el bosó de Higgs té una massa d'uns P11.3) Suposant
que el bosó de Higgs té una massa d'uns 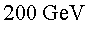 ,
estimeu la quantitat de bosons de Higgs que es produirien després
d'1 any produint
col•lisions a ,
estimeu la quantitat de bosons de Higgs que es produirien després
d'1 any produint
col•lisions a  amb una lluminositat instantània de
amb una lluminositat instantània de 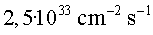 . .
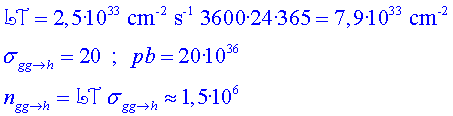
 P11.4) Suposant
que la massa del bosó de Higgs fos superior a P11.4) Suposant
que la massa del bosó de Higgs fos superior a 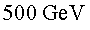 ,
quins són els canals en què es pot desintegrar? Vol dir això
que és impossible que es desintegri en qualsevol altre canal? ,
quins són els canals en què es pot desintegrar? Vol dir això
que és impossible que es desintegri en qualsevol altre canal?

Vol dir que la probabilitat de desintegra-se
en els altres canals és molt baixa però no exactament
zero.
 P11.5) Estimeu
a partir de la figura 9 i del resultat de la pregunta P11.4
el nombre de parells P11.5) Estimeu
a partir de la figura 9 i del resultat de la pregunta P11.4
el nombre de parells 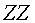 que es van produir durant aquest període. Creieu que és un
nombre suficientment alt per treure una bona estadística?
que es van produir durant aquest període. Creieu que és un
nombre suficientment alt per treure una bona estadística?


|

 6/8
6/8 






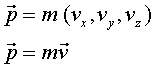
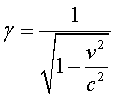






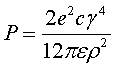



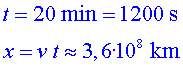
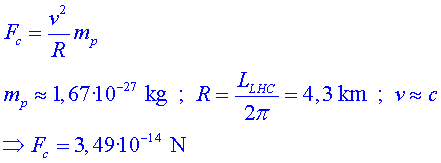
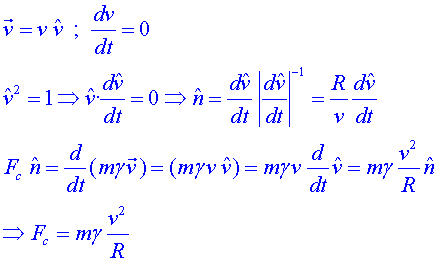

 és el factor
relativista introduït en la propera secció. Aquest és
el resultat que s'ha d'utilitzar per calcular el camp magnètic dels
imans.
és el factor
relativista introduït en la propera secció. Aquest és
el resultat que s'ha d'utilitzar per calcular el camp magnètic dels
imans.