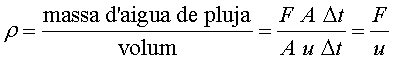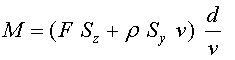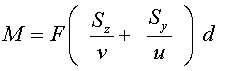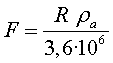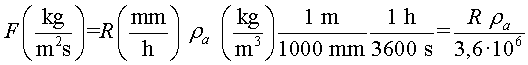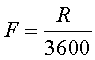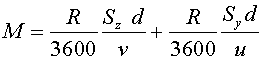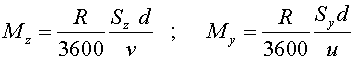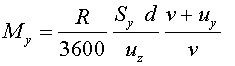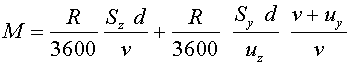núm 16 |
Tardor 2015 |
Societat Catalana de Física |
| Inici |
| Sumari |   8/8 8/8 |
| El racó obscur:
Corre que plou! Xavier Bohigas |
|
| En aquest article analitzem el problema de si és millor córrer o caminar lentament sota la pluja per mullar-nos el mínim possible. Es tracta d'un problema que ha atret l'atenció de molts científics i que ha estat molt debatut. Presentem la resolució en diverses situacions: sense vent, amb vent de cara, amb vent posterior i amb vent lateral. Es modelitza la persona que camina sota la pluja com un paral•lelepípede. Amb el resultat obtingut podem determinar la quantitat d'aigua, en massa, que recollirà cadascuna de les superfícies de la persona que camina sota la pluja. |
IntroduccióQuan plou, la gent, habitualment, es posa a córrer per
intentar mullar-se el mínim possible. És una reacció bastant
automàtica. Però és correcta aquesta reacció o és
millor caminar a poc a poc per no mullar-se? En aquest article hem elaborat
un model relativament senzill amb el qual podem resoldre aquest dilema de forma
clara. Cas 1: pluja amb caiguda vertical
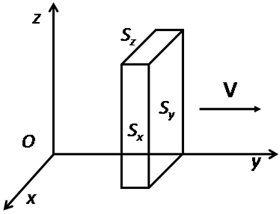
Primer de tot definirem els paràmetres que descriuen el nostre problema, tant els relatius a la persona que camina sota la pluja com els relatius a la mateixa pluja. Respecte a la persona: modelitzarem la persona com un paral•lelepípede.
Nomenarem Respecte a la pluja: Nomenem
Ja que,
Si la persona recorre una distància
Que, utilitzant l’equació (1), podem escriure com:
Una dada que sol trobar-se en la informació meteorològica
general és la intensitat de volum d'aigua o intensitat de precipitació
(que habitualment es dóna en mil•límetres d'aigua caiguda en una
hora), també anomenada ritme de precipitació, que representarem
amb
on
Si en l’expressió (4) substituïm
la densitat de l’aigua,
on
on les superfícies
amb:
on
És clar que, si la persona es desplaça ràpidament,
la quantitat d'aigua recollida per la seva superfície frontal ( Cas 2: pluja amb vent frontalConsiderem el segon cas. Suposarem que bufa vent en contra del sentit del moviment de la persona que camina sota la pluja. És a dir, que té vent de cara. La situació és equivalent a considerar que la velocitat de la pluja té dos components, un component dirigit segons la vertical (igual que en el cas 1) i un altre component horitzontal (que equival al vent frontal). Així, podem expressar la velocitat de les gotes de pluja, en el nostre sistema de referència, amb:
La quantitat d'aigua que la persona que camina rep sobre la seva superfície superior serà la mateixa que en el cas 1, és a dir:
Per calcular la quantitat d'aigua que impacta sobre la superfície
frontal de la persona, podem fer un raonament anàleg al cas 1. Només
hem de tenir en compte que la velocitat relativa de la gota d'aigua respecte
a la persona que camina és, en aquest cas,
Així, la quantitat total d'aigua que recull la persona
(en kg) serà
Veiem que, en aquest cas 2 de pluja amb vent frontal, la quantitat
d'aigua recollida tant per la superfície frontal com per la superfície
superior de la persona que camina depenen de la velocitat del caminant,
on es veu clarament que la quantitat d'aigua total que recull
la persona que camina disminueix en augmentar la seva velocitat de desplaçament,
|
| |
(11) |
La quantitat d'aigua que la persona que camina rep sobre la seva superfície superior tornarà a ser la mateixa que en els dos casos anteriors, 1 i 2. És a dir:
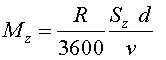 |
I, per calcular la quantitat d'aigua recollida a la superfície vertical hem d'analitzar dues situacions diferents:
1) si el mòdul de la velocitat de la
persona que camina és més petit que la velocitat del vent, ![]() ,
i
,
i
2) si el mòdul de la velocitat de la
persona que camina és més gran que la velocitat del vent, ![]() .
.
En la primera situació, ![]() ,
es mulla l'esquena de la persona que camina. Mentre que en la segona situació,
,
es mulla l'esquena de la persona que camina. Mentre que en la segona situació,
![]() , serà la part
davantera la que quedi mullada. Analitzem tots dos casos per separat.
, serà la part
davantera la que quedi mullada. Analitzem tots dos casos per separat.
Si ![]() , la component horitzontal
de la velocitat relativa de la gota d'aigua respecte del caminant serà
, la component horitzontal
de la velocitat relativa de la gota d'aigua respecte del caminant serà
![]() . I, fent un raonament
anàleg al del cas 2, la quantitat total d'aigua que recull la persona
(en
. I, fent un raonament
anàleg al del cas 2, la quantitat total d'aigua que recull la persona
(en ![]() ) serà:
) serà:
 |
(12) |
equació que reescriurem com:
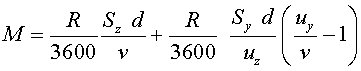 |
(13) |
on es veu clarament que la quantitat d'aigua recollida per
la persona que camina sota la pluja és una funció decreixent respecte
de la seva velocitat de desplaçament, ![]() .
Per tant, si aquesta persona vol mullar-se el mínim possible haurà
de desplaçar-se tan ràpidament com pugui. Quan la velocitat de
la persona,
.
Per tant, si aquesta persona vol mullar-se el mínim possible haurà
de desplaçar-se tan ràpidament com pugui. Quan la velocitat de
la persona, ![]() , coincideixi
amb la velocitat del vent,
, coincideixi
amb la velocitat del vent, ![]() ,
la quantitat d'aigua que recull en la seva superfície vertical,
,
la quantitat d'aigua que recull en la seva superfície vertical, ![]() ,
serà nul•la i només recull aigua a la superfície superior,
,
serà nul•la i només recull aigua a la superfície superior,
![]() . Aquesta velocitat
serà la màxima velocitat a la qual pot desplaçar-se la
persona en el nostre rang de validesa, donat per la condició
. Aquesta velocitat
serà la màxima velocitat a la qual pot desplaçar-se la
persona en el nostre rang de validesa, donat per la condició ![]() .
.
En la segona situació, quan es compleix ![]() ,
el caminant va a una velocitat superior a la velocitat del vent, l'aigua de
pluja arribarà a la superfície anterior del caminant, mentre que
la seva esquena quedarà completament seca. I la velocitat relativa de
la gota de pluja respecte del caminant serà
,
el caminant va a una velocitat superior a la velocitat del vent, l'aigua de
pluja arribarà a la superfície anterior del caminant, mentre que
la seva esquena quedarà completament seca. I la velocitat relativa de
la gota de pluja respecte del caminant serà ![]() .
Seguint un raonament anàleg a l’anterior, obtenim que la quantitat d'aigua
que recull la persona que camina sota la pluja amb una velocitat superior a
la del vent posterior és
.
Seguint un raonament anàleg a l’anterior, obtenim que la quantitat d'aigua
que recull la persona que camina sota la pluja amb una velocitat superior a
la del vent posterior és
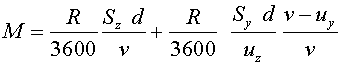 |
(14) |
o bé:
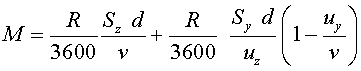 |
(15) |
Es pot comprovar fàcilment que si la persona es desplaça amb una velocitat igual a la del vent només es mulla la superfície superior, i el valor coincideix amb l'obtingut amb l'equació (13).
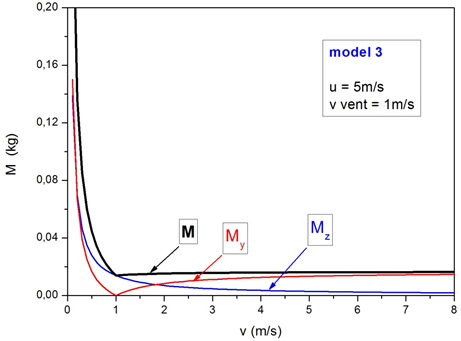 |
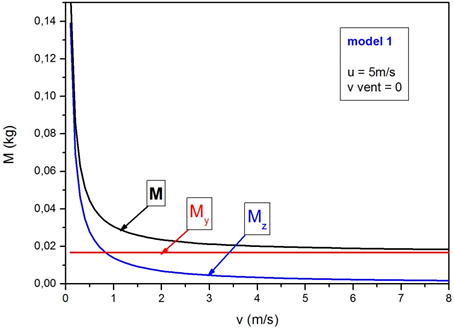
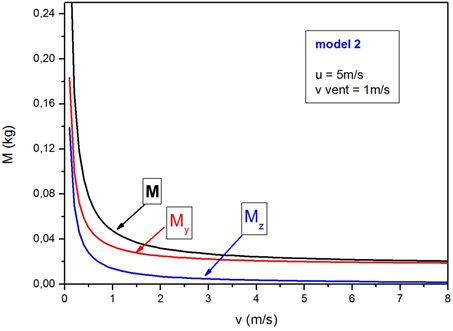
| Fig. 4: Quantitat d'aigua que rep una persona que es desplaça
sota la pluja vertical i amb vent (de velocitat |
Les funcions matemàtiques que corresponen a la quantitat
d'aigua recollida per la superfície vertical, ![]() ,
de la persona que es desplaça sota la pluja,
,
de la persona que es desplaça sota la pluja, ![]() ,
són explicitades pels segons sumands de les equacions (12) i (14). És
evident que els valors negatius d’aquesta variable
,
són explicitades pels segons sumands de les equacions (12) i (14). És
evident que els valors negatius d’aquesta variable ![]() no tenen cap sentit físic, en el nostre problema. Per tant, només
haurem de tenir en compte la part positiva d’aquestes funcions. Cal dir que
la funció
no tenen cap sentit físic, en el nostre problema. Per tant, només
haurem de tenir en compte la part positiva d’aquestes funcions. Cal dir que
la funció ![]() ,
corresponent al cas que
,
corresponent al cas que ![]() ,és
una funció creixent, segons podem veure a l’equació (15).
,és
una funció creixent, segons podem veure a l’equació (15).
A la figura 4 hem representat la dependència de la quantitat d'aigua
que recull una persona respecte a la seva velocitat de desplaçament,
![]() . La gràfica
correspon a la situació numèrica següent: la persona recorre
. La gràfica
correspon a la situació numèrica següent: la persona recorre
![]() , sota una pluja que
cau verticalment a una velocitat
, sota una pluja que
cau verticalment a una velocitat ![]() i amb un vent posterior de
i amb un vent posterior de ![]() .
A la mateixa gràfica estan representades les masses d'aigua recollides
en la seva superfície superior,
.
A la mateixa gràfica estan representades les masses d'aigua recollides
en la seva superfície superior, ![]() ,
i en la seva superfície vertical,
,
i en la seva superfície vertical, ![]() .
Observem que la quantitat d'aigua que recull sobre la seva superfície
superior,
.
Observem que la quantitat d'aigua que recull sobre la seva superfície
superior, ![]() , (línia
de color blau) disminueix en augmentar la velocitat de desplaçament,
, (línia
de color blau) disminueix en augmentar la velocitat de desplaçament,
![]() . Pel que fa a la quantitat
d'aigua recollida sobre la superfície vertical de la persona (línia
de color vermell), veiem que quan la velocitat de la persona és inferior
a la velocitat del vent (
. Pel que fa a la quantitat
d'aigua recollida sobre la superfície vertical de la persona (línia
de color vermell), veiem que quan la velocitat de la persona és inferior
a la velocitat del vent (![]() ,
amb
,
amb ![]() en aquest cas),
la quantitat d'aigua recollida disminueix en augmentar la seva velocitat de
desplaçament. Però, si la persona es desplaça a velocitats
superiors a la velocitat del vent (
en aquest cas),
la quantitat d'aigua recollida disminueix en augmentar la seva velocitat de
desplaçament. Però, si la persona es desplaça a velocitats
superiors a la velocitat del vent (![]() ),
la quantitat d'aigua recollida sobre aquesta superfície creixerà
lleugerament quan augmenti la seva velocitat de desplaçament.
),
la quantitat d'aigua recollida sobre aquesta superfície creixerà
lleugerament quan augmenti la seva velocitat de desplaçament.
Quan la velocitat de desplaçament de la persona que es mou sota la pluja
coincideix amb la velocitat del vent (![]() )
no es mullarà ni la l'esquena ni la part anterior. Únicament es
mullarà la superfície superior (espatlles i cap), situació
que correspon a aquella en què la quantitat d'aigua recollida per la
persona serà mínima.
)
no es mullarà ni la l'esquena ni la part anterior. Únicament es
mullarà la superfície superior (espatlles i cap), situació
que correspon a aquella en què la quantitat d'aigua recollida per la
persona serà mínima.
Cas 4: pluja amb vent lateral
Completem la nostra anàlisi suposant que existeix vent lateral dirigit contra la persona que camina sota la pluja. És a dir que la velocitat de les gotes de pluja es podrà escriure:
| |
(16) |
La quantitat d'aigua que rep aquesta superfície lateral
en un temps ![]() serà
igual a
serà
igual a ![]() Tenint en
compte que
Tenint en
compte que ![]() i realitzant
uns càlculs anàlegs als que hem fet més amunt es dedueix
que
i realitzant
uns càlculs anàlegs als que hem fet més amunt es dedueix
que
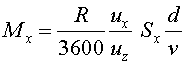 |
(17) |
Veiem que la quantitat d'aigua disminueix amb la velocitat
de desplaçament de la persona.
Per saber la quantitat d'aigua que cau sobre la persona que camina sota la pluja
amb vent frontal i lateral, hauríem de sumar l’equació (16)
a l’equació (10). En el cas que el vent estigui dirigit
cap a la part posterior de la persona i tingui un component lateral, hauríem
de fer una discussió anàloga a la que hem fet en el cas 3, afegint-hi
el sumand que dóna l’equació (16).
Conclusions
Hem analitzat el problema plantejat sobre com es pot recórrer
una certa distància sota la pluja mullant-nos el mínim possible.
Per a això hem deduït la funció que ens dóna la quantitat
d'aigua recollida per una persona que es desplaça sota la pluja, en diferents
situacions. En el cas més simple, és a dir, que la pluja cau verticalment
i no hi ha vent, la solució obtinguda indica que la millor estratègia
per mullar-se el mínim possible consisteix a córrer al més
ràpidament possible. Si bé hem de tenir en compte que d'aquesta
manera només aconseguirem reduir la quantitat d'aigua que cau sobre la
nostra superfície superior, ja que la quantitat d'aigua recollida per
la nostra superfície frontal serà independent de la nostra velocitat.
Si a més hi ha vent, hem atacat el problema en tres situacions diferents.
En el cas que el vent sigui frontal a la persona que camina sota la pluja, hem
vist que, també en aquest cas, la millor estratègia per mullar-nos
poc és desplaçar-nos tan de pressa com sigui possible. En aquest
cas, en desplaçar-nos ràpidament reduirem tant la quantitat d'aigua
que arriba a la nostra part frontal com la que ens cau sobre el cap i les espatlles.
En el cas que el vent bufi contra la nostra esquena, hi ha una velocitat en
què la quantitat d'aigua recollida pel nostre cos és mínima.
Aquesta velocitat coincideix amb la velocitat del vent. En aquest cas, només
ens mullarem cap i espatlles, de manera que les nostres superfícies frontal
i posterior es mantindran seques.
A les dues situacions en què hi hagi vent de cara o d'esquena, haurem
d'afegir un sumand si, a més, hi ha vent lateral. La quantitat d'aigua
que mullarà la nostra superfície lateral és inversament
proporcional a la nostra velocitat de desplaçament.
L'anàlisi que hem realitzat es podria ampliar incorporant-hi altres elements
que canviarien les condicions del problema plantejat. Per exemple, quan una
persona corre s'inclina lleugerament cap endavant, de manera que les dues superfícies
frontal i superior varien. L'ús de paraigües per protegir-nos de
la pluja també faria diferent la resolució del problema.