IntroduccióLa cinemàtica té una reconeguda fama de tema àrid i desmotivador. Posicions, temps, velocitats i acceleracions, en una o diverses dimensions, en trajectòries rectes, circulars, parabòliques... s'apliquen a mòbils puntuals i del tot abstractes, en una aproximació necessàriament matemàtica, però que no hauria de separar-se de les situacions físiques.
Aquests problemes empaquetats us proposen un seguit de problemes de «moviment» referits a cada un dels continguts del currículum de batxillerat i aplicats a situacions ben variades, que esperem que us suggereixin noves aproximacions a aquest tema i nous recursos per utilitzar.
Full de l'alumnat
Els problemes
| El moviment
1: Anàlisi de moviments reals, uniformes o no,
utilitzant equips de captació de dades, programes d'anàlisi
de vídeo digital o altres procediments experimentals. Coneixement
de les magnituds del moviment: sistema de referència, posició,
desplaçament, velocitat i acceleració (en una i dues dimensions)
en contextos reals.
|
1. Un estudiant (vegeu
la figura 2) va recollir dades sobre les caigudes d'objectes de diferents formes
per fer un treball de recerca sobre l'aerodinàmica dels cossos en caiguda
lliure. Va filmar les caigudes i en va analitzar les dades a partir de les gravacions.
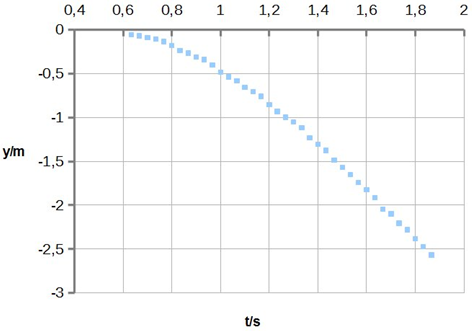
Les dades recollides es presenten en aquest gràfic.
 |
 |
| Fig. 1: Fotograma de la gravació feta per Albert Fuentemilla
|
Fig. 2: |
a) Indica la durada
i el desplaçament de la caiguda enregistrada i la velocitat mitjana.
b) On va situar l'estudiant l'origen
de coordenades? I l'origen dels temps?
c) Es tracta d'un moviment uniforme
o d'un moviment accelerat? Detalla la resposta (pots incloure dades sobre
la velocitat i/o l'acceleració).
| El moviment
2: Anàlisi quantitativa
de moviments rectilinis amb velocitat o amb acceleració constant.
La caiguda lliure com a cas particular de moviment rectilini amb acceleració
constant. Anàlisi de moviments circulars uniformes emprant algun
programa de simulació (arc recorregut, angle girat, velocitat
angular, període i freqüència, relació entre
velocitat angular i lineal, i acceleració centrípeta).
|
2. A la Universitat de Bremen hi ha la ZARM Drop Tower,
una torre de 146 metres d'altura. Els investigadors deixen caure «càpsules
de caiguda» equipades amb càmeres i tota mena de sensors per un
tub d'acer sense aire dins de la torre. Mentre dura la caiguda lliure dins de
la càpsula es realitzen experiments de microgravetat.
a) A causa de limitacions
tècniques, la caiguda lliure és «només» de
120 m. Calcula
de quant temps disposem per a cada experiment quan deixem caure una càpsula
b) A quina velocitat
arriba la càpsula al final de la caiguda lliure?
c) La base del tub
de caiguda està dissenyada per amortir l'impacte. Tot i això,
la càpsula experimenta una desceleració de 50 g. Calcula la
distància de frenada.
Dada: g
= 9,81 m·s-2
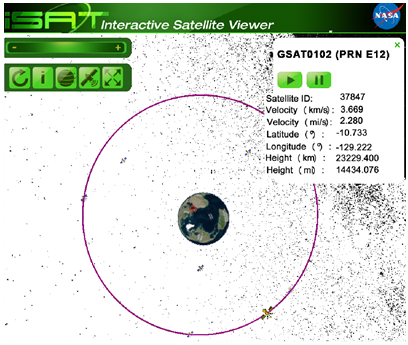
3. A la pàgina
web http://science.nasa.gov/iSat
podeu trobar la situació de moltíssims satèl•lits.
Els podeu seleccionar pel nom o clicant la figura. A la imatge del costat es
veu la pantalla que correspon a un dels satèl•lits Galileo PRN
E12 (el nom és Natalia), amb una òrbita pràcticament
circular. Amb les dades que apareixen al requadre i sabent que el radi de la
Terra és de 6.378,1
km
 |
| Fig. 4 |
a) Calcula la velocitat
angular i el període del moviment d'aquest satèl•lit.
b) L'acceleració centrípeta
del satèl•lit equival a la gravetat a l'altura a la qual es mou.
Calcula-la.
c) Natalia
va ser llançat el 21 d'octubre de 2011. Quantes voltes ha fet fins
ara?
d) Busca un altre
satèl•lit, amb una òrbita circular, però que vagi
a menys altura. Anota’n les dades rellevants i argumenta, sense fer
càlculs, si la seva velocitat angular i el seu període són
més grans, més petits o iguals que el del Galileo PRN E12.
| El moviment 3:
Estudi experimental d'un moviment parabòlic.
Els moviments en dues dimensions com a composició de dos moviments.
|
4. Les puces són
reconegudes per la seva gran capacitat per fer salts. Tot i la seva mida reduïda
(uns 2 mm) i l'absència
d'ales, la seva supervivència depèn dels salts que fan d'hoste
en hoste. Les puces de gos poden saltar fins a una altura de 25
cm i les puces de gat fins a 17
cm.
 |
| Fig. 5 |
a) Considera que
aconsegueixen la màxima altura saltant verticalment. Quina és
la velocitat màxima de sortida en el seu salt?
Si situem les puces sobre una superfície horitzontal
i les fem saltar amb la mateixa velocitat inicial que has calculat a l'apartat
anterior, però en un angle de 45º,
b) Quant temps durarà
el seu salt (en cada cas)?
c) Quina serà
la màxima altura assolida?
d) Calculeu l'abast
del seu salt.
S'ha dit que si els humans tinguéssim la mateixa capacitat
«saltadora» que les puces podríem fer salts de centenars
de metres de llargada.
e) Quin abast tindria
el salt d'una persona amb la mateixa velocitat de sortida que una puça?
f) Quina o quines
magnituds de les següents són molt més grans en el salt
d'una puça que en el d'una persona?
- abast
- altura màxima
- temps de vol
- acceleració en l'etapa de propulsió
5. Estem dissenyant
un petit videojoc i volem fer els salts realistes, de manera que segueixin les
lleis del moviment en dues dimensions.
El nostre personatge salta de plataforma en plataforma, amb una velocitat de
sortida variable pel que fa a mòdul i a angle (l'angle pot variar entre
0 º i 60º).
Hi ha 3 nivells de plataformes situades a 1, 2 i 3 metres d'altura.
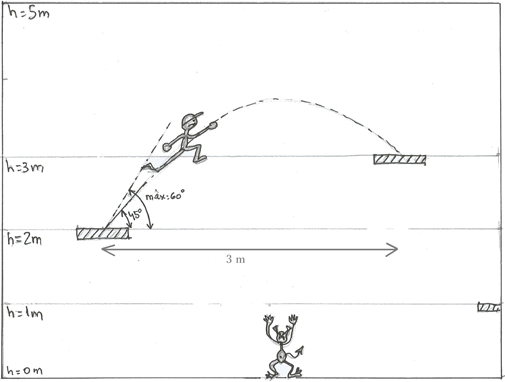 |
| Fig. 6 |
a) Volem limitar
el mòdul de la velocitat perquè el personatge mai no desaparegui
per l'extrem superior de la pantalla (en cap moment no ha de superar els
5 metres d'altura) . Quina ha de ser la velocitat màxima?
b) Volem que
el nostre personatge salti de la primera a la segona plataforma (vegeu
l'esquema) sortint amb un angle de 45º.
Quina velocitat de sortida ha de tenir?
c) Un personatge
«malvat» de 0,80
m d'altura salta verticalment des del nivell h
= 0.
Volem que «just no arribi» a tocar el nostre personatge en
el punt més alt del seu salt. Amb quina velocitat ha d'iniciar
el seu salt el petit dimoni?
d) En un nivell
avançat hi ha el mode «sense gravetat». Com han de
ser els mòduls i les direccions de la velocitat per saltar d'una
plataforma a l'altra en aquest nivell? Què li passarà al
dimoniet quan salti?
| El moviment
4: Representació del
moviment a través de llenguatge gràfic, verbal i matemàtic,
i relació entre les diferents representacions. Interpretació
de les diferents representacions del moviment (gràfica, verbal,
matemàtica) i utilització d'aquestes representacions per
resoldre problemes. Comunicació dels resultats dels experiments
de manera ordenada i utilitzant el vocabulari específic i les
eines informàtiques (fulls de càlcul, generadors de gràfics,
processadors de textos, etc.) adients.
|
6.Bloodhound és
el nom d'un prototip de cotxe supersònic dissenyat per superar la velocitat
de 1000 mi/h en pista
(mi = milla).
Està equipat d'un motor a
 |
| Fig. 7 |
reacció que li donarà un primer impuls i un coet
que l'accelerarà fins a la velocitat màxima. També són
importants els diferents sistemes de frenada.
Hem consultat les dades del prototip a:
d'on hem copiat aquesta taula (compte, els anglesos fan un ús dels
punts i les comes diferent del que fem nosaltres!).
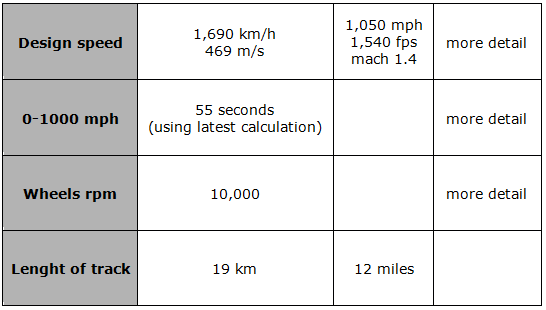 |
| Taula 1: mph
= milles/ hora. rpm
= revolucions/ minut. |
Amb aquestes dades:
a) Calcula la distància
que recorre mentre accelera fins a 1690
km/h i compara-la amb la longitud de la pista (suposa que accelera
uniformement).
b) Els diferents sistemes de frenada
actuen des del moment en què s'ha assolit la velocitat màxima,
de manera que l'acceleració de frenada sigui aproximadament constant
i que el vehicle s'aturi al final de la pista. Quant temps tardarà
a frenar?
c) Fes un gràfic x-t
i un gràfic v-t
del moviment.
d) Quin deu ser el
radi de les rodes? Calcula l'acceleració centrípeta als punts
exteriors de les rodes.
Dada : 1
mi=1 milla = 1609 m
7.Els smartphones
(telèfons intel•ligents) porten incorporat un sensor d'acceleració
o acceleròmetre, útil per a aplicacions en les quals l'orientació
o el moviment del telèfon és important. És fàcil
 |
| Fig. 8 |
trobar aplicacions que ens permeten conèixer les lectures
d'aquests acceleròmetres i mesurar les acceleracions.
Amb una d'aquestes apps instal•lada en un smartphone, uns estudiants
han pujat a un autobús i, amb molta cura perquè el mòbil
estigui ben horitzontal i alineat amb l'eix de l'autobús, han recollit
les dades del sensor, començant quan el bus estava aturat en una parada
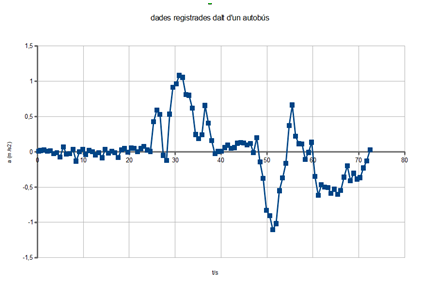
i acabant quan s'aturava en un semàfor. Les dades, passades a un full
de càlcul, els han donat aquest gràfic.
.
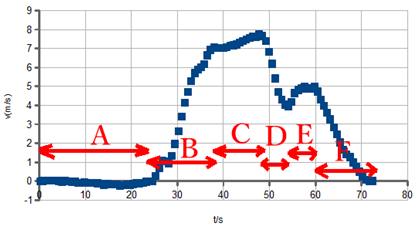
a) Descriu el moviment
de l'autobús a partir d'aquestes dades. Fes-ho dividint el moviment
en diferents etapes. Pots començar, per exemple: «Etapa A:
durant els primeres 25
segons l'autobús està parat...».
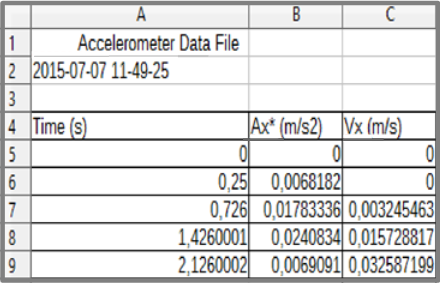
Amb les dades al full de càlcul, i sabent que la velocitat
inicial era zero, han calculat les velocitats. Al costat es veu un fragment
del full de càlcul.
 |
| Taula 2 |
b) Quina fórmula
han utilitzat per calcular les velocitats en el full de càlcul?
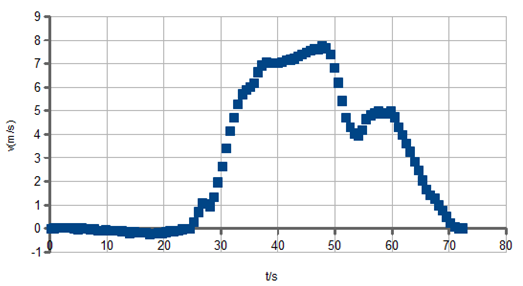
c) Amb la nova columna
del full de càlcul s'obté el gràfic v-t.
Identifica en aquest gràfic cada una de les etapes que has utilitzat
en la descripció a l'apartat a.
 |
| Fig. 9 |
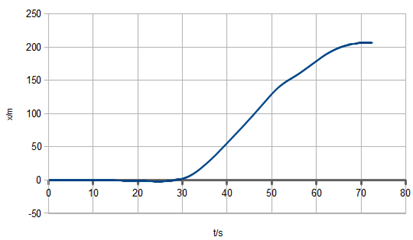
d) (Extra) Com hauria
de ser la fórmula per calcular les posicions en una nova columna? Fes
una predicció aproximada de la forma del gràfic
x-t que en resultaria.

  
Solucions
Els problemes
1. Un estudiant (
vegeu la figura 2) va recollir dades sobre les caigudes d'objectes de diferents
formes per a fer un treball de recerca sobre l'aerodinàmica dels cossos
en caiguda lliure. Va filmar les caigudes i en va analitzar les dades a partir
de les gravacions. Les dades recollides es presenten en aquest gràfic.
a) Indica la durada
i el desplaçament de la caiguda enregistrada i la velocitat mitjana.
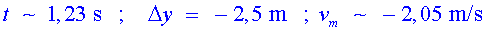
b) On va situar l'estudiant l'origen
de coordenades? I l'origen dels temps?
Origen coordenades: on l'estudiant va
deixar caure el cartró (a dalt). Origen dels temps: 0,63
segons abans de començar la caiguda.
c) Es tracta d'un moviment uniforme
o d'un moviment accelerat? Detalla la resposta (pots incloure dades sobre
la velocitat i/o l'acceleració).
Al principi és accelerat i al final
és uniforme. L'acceleració va disminuint, per exemple entre
0,63 i 1,00
s 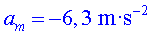 . L'acceleració
segueix disminuint (el valor absolut) fins que entre 1,4
s i el final el moviment és pràcticament uniforme . L'acceleració
segueix disminuint (el valor absolut) fins que entre 1,4
s i el final el moviment és pràcticament uniforme 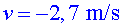 (aproximadament).
(aproximadament).
2. A la Universitat de Bremen hi ha la ZARM Drop Tower,
una torre de 146 metres d'altura. Els investigadors deixen caure «càpsules
de caiguda» equipades amb càmeres i tota mena de sensors per un
tub d'acer sense aire dins de la torre. Mentre dura la caiguda lliure dins de
la càpsula es realitzen experiments de microgravetat.
a) A causa de limitacions
tècniques, la caiguda lliure és «només» de
120 m. Calcula
de quant temps disposem per a cada experiment quan deixem caure una càpsula
4,95 s
b) A quina velocitat
arriba la càpsula al final de la caiguda lliure?
48,5 m/s (cap avall)
c) La base del tub
de caiguda està dissenyada per amortir l'impacte. Tot i això
la càpsula experimenta una desceleració de 50 g. Calcula la
distància de frenada.
48,5
m/s (cap amunt) ; 9,89
s
3.A la pàgina
web http://science.nasa.gov/iSat
podeu trobar la situació de moltíssims satèl•lits.
Els podeu seleccionar pel nom o clicant la figura. A la imatge del costat es
veu la pantalla que correspon a un dels satèl•lits Galileo PRN
E12 (el nom és Natalia), amb una òrbita pràcticament
circular. Amb les dades que apareixen al requadre i sabent que el radi de la
Terra és de 6.378,1
km
a) Calcula la velocitat
angular i el període del moviment d'aquest satèl•lit.
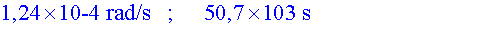
b) L'acceleració centrípeta
del satèl•lit equival a la gravetat a l'altura a la que es mou.
Calcula-la.

c) Natalia va ser
llançat el 21 d'octubre de 2011. Quantes voltes ha fet fins ara?
Depèn de quan es contesti: per
al 21 d'octubre de 2015, 2490
voltes
d) Busca un altre
satèl•lit, amb una òrbita circular, però que vagi
a menys altura. Anota’n les dades rellevants i argumenta, sense fer
càlculs, si la seva velocitat angular i el seu període són
més grans, més petits o iguals que el del Galileo PRN E12..
Qualsevol
satèl•lit d'òrbita circular amb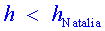 (i, per tant,
(i, per tant, 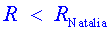 )
la velocitat és )
la velocitat és 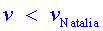 . Com que
. Com que 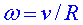 , necessàriament , necessàriament
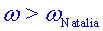 . Com que . Com que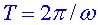 , del resultat anterior es dedueix que
, del resultat anterior es dedueix que 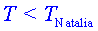
4. Les puces són
reconegudes per la seva gran capacitat per fer salts. Tot i la seva mida reduïda
(uns 2 mm) i l'absència
d'ales, la seva supervivència depèn dels salts que fan d'hoste
en hoste. Les puces de gos poden saltar fins a una altura de 25
cm i les puces de gat fins a 17
cm.
a) Considera que
aconsegueixen la màxima altura saltant verticalment. Quina és
la velocitat màxima de sortida en el seu salt?
p.gos: 2,21
m/s; p.gat: 1,83 m/s
Si situem les puces sobre una superfície horitzontal
i les fem saltar amb la mateixa velocitat inicial que has calculat a l'apartat
anterior, però en un angle de 45º:
b) Quant temps durarà
el seu salt (en cada cas)?
p. gos 0,319
s; p. gat: 0,264
s
c) Quina serà
la màxima altura assolida?
p. gos: 12,5
cm; p. gat: 8,5
cm
d) Calculeu l'abast
del seu salt.
p. gos: 50
cm; p. gat: 34
cm
S'ha dit que si els humans tinguéssim la mateixa capacitat
«saltadora» que les puces podríem fer salts de centenars
de metres de llargada.
e) Quin abast tindria
el salt d'una persona amb la mateixa velocitat de sortida que una puça?
El
mateix que la puça
f) Quina o quines
magnituds de les següents són molt més grans en el salt
d'una puça que en el d'una persona?
- abast
- altura màxima
- temps de vol
- acceleració en l'etapa de propulsió
Acceleració en l'etapa de propulsió (ja
que les seves potes són molt més curtes)
5. Estem dissenyant
un petit videojoc i volem fer els salts realistes, de manera que segueixin les
lleis del moviment en dues dimensions.
El nostre personatge salta de plataforma en plataforma, amb una velocitat de
sortida variable pel que fa a mòdul i a angle (l'angle pot variar entre
0 º i 60º).
Hi ha 3 nivells de plataformes situades a 1, 2 i 3 metres d'altura.
a) Volem limitar
el mòdul de la velocitat perquè el personatge mai no desaparegui
per l'extrem superior de la pantalla (en cap moment no ha de superar els
5 metres d'altura) . Quina ha de ser la velocitat màxima?
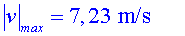
b) Volem que
el nostre personatge salti de la primera a la segona plataforma (vegeu
l'esquema) sortint amb un angle de 45º.
Quina velocitat de sortida ha de tenir?
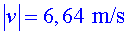 o bé
o bé 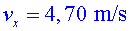 ; ;
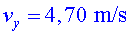
c) Un personatge
«malvat» de 0,80
m d'altura salta verticalment des del nivell h
= 0.
Volem que «just no arribi» a tocar el nostre personatge en
el punt més alt del seu salt. Amb quina velocitat ha d'iniciar
el seu salt el petit dimoni?
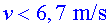
d) En un nivell
avançat hi ha el mode «sense gravetat». Com han de
ser els mòduls i les direccions de la velocitat per a saltar d'una
plataforma a l'altra en aquest nivell? Què li passarà al
dimoniet quan salti?
Els mòduls no importen.
Només importen les direccions (el personatge anirà en línia
recta). En el cas de les plataformes de la figura, un angle de 18,4º
estarà bé. El dimoniet saltarà cap amunt amb velocitat
constant i desapareixerà per dalt després del primer salt
si no ha agafat l'intrèpid protagonista.
6.Bloodhound és
el nom d'un prototip de cotxe supersònic dissenyat per superar la velocitat
de 1000 mi/h en pista
(mi=milla).
Està equipat d'un motor a
reacció que li donarà un primer impuls i un coet
que l'accelerarà fins a la velocitat màxima. També són
importants els diferents sistemes de frenada.
Hem consultat les dades del prototip a:
d'on hem copiat aquesta taula (compte, els anglesos fan un ús dels
punts i les comes diferent del que fem nosaltres!).
 |
| Taula 1: mph=milles/
hora. rpm=revolucions/
minut. |
Amb aquestes dades:
a) Calcula la distància
que recorre mentre accelera fins a 1690
km/h i compara-la amb la longitud de la pista (suposa que accelera
uniformement).
13,56
km (representa el 71%
del total de la pista)
b) Els diferents sistemes de frenada
actuen des del moment en què s'ha assolit la velocitat màxima,
de manera que l'acceleració de frenada sigui aproximadament constant
i que el vehicle s'aturi al final de la pista. Quant temps tardarà
a frenar?
23,2
s
c) Fes un gràfic x-t
i un gràfic v-t
del moviment.
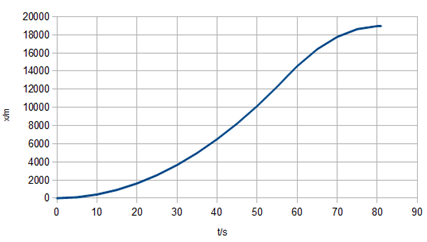 |
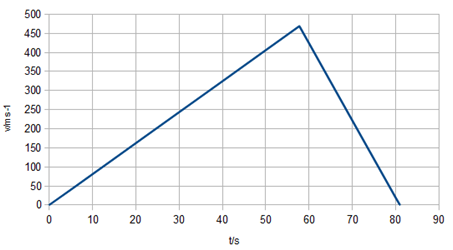 |
| Fig. 10 |
Fig. 11 |
d) Quin deu ser el
radi de les rodes? Calcula l'acceleració centrípeta als punts
exteriors de les rodes.
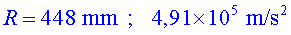 (
(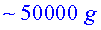 !) !)
7.Els smartphones
(telèfons intel•ligents) porten incorporat un sensor d'acceleració
o acceleròmetre, útil per a aplicacions en les quals l'orientació
o el moviment del telèfon és important. És fàcil
trobar aplicacions que ens permeten conèixer les lectures d'aquests acceleròmetres
i mesurar les acceleracions.
Amb una d'aquestes apps instal•lada en un smartphone, uns estudiants
han pujat a un autobús i, amb molta cura perquè el mòbil
estigui ben horitzontal i alineat amb l'eix de l'autobús, han recollit
les dades del sensor, començant quan el bus estava aturat en una parada
i acabant quan s'aturava en un semàfor. Les dades, passades a un full
de càlcul, els han donat aquest gràfic.
a) Descriu el moviment
de l'autobús a partir d'aquestes dades. Fes-ho dividint el moviment
en diferents etapes. Pots començar, per exemple: «Etapa A:
durant els primeres 25
segons l'autobús està parat...».
Etapa A:
durant els primers 25
segons l'autobús està parat (enunciat). Etapa B:
entre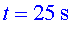 i i 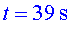 l'autobús accelera a sotragades (en fa 3, la segona la més important). Etapa
C: entre
l'autobús accelera a sotragades (en fa 3, la segona la més important). Etapa
C: entre 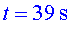 s i
s i 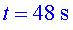 avança amb velocitat
gairebé constant (amb una acceleració positiva molt petita). Etapa D:
entre avança amb velocitat
gairebé constant (amb una acceleració positiva molt petita). Etapa D:
entre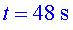 i i 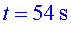 fa una frenada relativament forta. Etapa E:
entre
fa una frenada relativament forta. Etapa E:
entre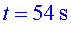 i i 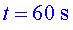 torna a augmentar la velocitat una mica. Etapa F:
entre
torna a augmentar la velocitat una mica. Etapa F:
entre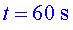 i i  frena suaument fins a (segons l'enunciat) quedar-se parat.
frena suaument fins a (segons l'enunciat) quedar-se parat.
Amb les dades al full de càlcul, i sabent que la velocitat
inicial era zero, han calculat les velocitats. Al costat es veu un fragment
del full de càlcul.
b) Quina fórmula
han utilitzat per a calcular les velocitats en el full de càlcul?
En C5
... «0»
; en C6, «=C5+B5*(A6-A5)»,
i totes les altres velocitats copiant la fórmula de C6
(pot discutir-se si s'utilitzaB5
o B6 com a valor de
l'acceleració en el càlcul de C6
o la mitjana de tots dos, però la diferència de resultats és
molt petita).
c) Amb la nova columna
del full de càlcul s'obté el gràfic v-t.
Identifica en aquest gràfic cada una de les etapes que has utilitzat
en la descripció a l'apartat a.
 |
 |
| Fig. 12 |
Fig. 13 |
d) (Extra) Com hauria
de ser la fórmula per calcular les posicions en una nova columna? Fes
una predicció aproximada de la forma del gràfic
x-t que en resultaria.
A la columna D
s'hauria d'afegir una fórmula, com ara
D5 = 0
D6 = D5 + C5*(A6-A5) + 0,5*(A6-A5)^2
i copiar-la a les següents.
| 
 7/8
7/8 






















