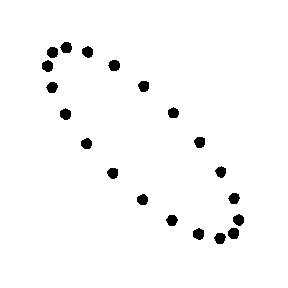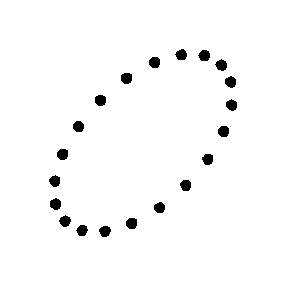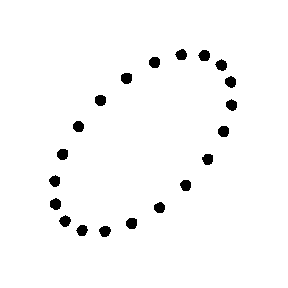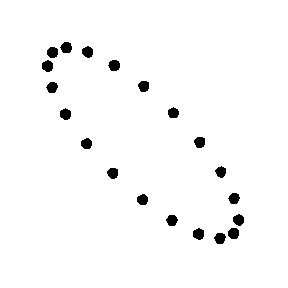Introducció
Què és una ona? Estem davant d'una qüestió
clàssica, de tots els temps. No és la nostra intenció repetir-nos.
Per què volem tractar aquest tòpic? Perquè encara es detecten
força malentesos al voltant de "què és una ona"
i perquè l'entrada en escena de les ones gravitacionals sembla que ha
revifat l'interès pel tema. En aquest cas, la pregunta seria: què
és una ona gravitacional? Si sabem què és una ona, podrem
o no saber què és una ona gravitacional? Estem segurs de saber
què és una ona electromagnètica? Vegem fins on arribem.
No és la nostra intenció ser sistemàtics ni rigorosos en
parlar d'ones. Només volem apuntar algunes idees que puguin servir per
ampliar les nostres exposicions al voltant d'aquest tema.
Ones mecàniques
 |
| Fig. 1: partícules test en un tub de Kundt. |
Les ones mecàniques són el paradigma de totes
les altres ones. La característica més important que tenen és
la de poder comptar, d'entrada, amb el que anomenem medi. El medi és
la substància que omple l'espai per on discorrerà l'ona. El medi
es caracteritza per una sèrie de magnituds físiques, com la densitat,
la temperatura, les tensions internes... Si "no passa res" diem que
el medi està en equilibri.
És important saber caracteritzar l'estat d'equilibri del medi, ja que
serà el referent a partir del qual podrem saber que passa alguna cosa.
Si no passa res el medi està quiet, les seves magnituds característiques
romanen constants en el temps. Per a una anàlisi introductòria
podem fer la simplificació que, en l'equilibri, les magnituds característiques
són també independents del punt del medi. I, si alguna de les
magnituds té caràcter vectorial, com les tensions internes, podem
simplificar-ho imposant que aquestes tensions són independents de la
direcció de l'espai. Un bon exemple de medi és la substància
aigua en repòs a l'interior d'una gran piscina o l'aire en calma dins
d'una habitació tancada. Qualsevol bloc gran de material sòlid
homogeni n'és també un bon exemple.
Quan no passa cap ona percebem el medi, en podem mesurar les
característiques: densitat, temperatura, etc., i observem que són
constants. El medi està en equilibri. Ens adonem que passa una ona perquè
les característiques del medi s'alteren respecte de l'equilibri. Deixen
de ser constants. L'alteració d'aquest estat d'equilibri és el
símptoma que alguna cosa passa, passa una ona.
Notem que també podem saber que el medi està en equilibri observant
que les petites porcions de medi romanen en repòs. Quan passa l'ona les
petites porcions de medi es posen en moviment. Pot ser difícil d'observar
directament, aquest moviment. El que es fa és utilitzar partícules
test. Un molt bon exemple on es fa servir aquest procediment és en l'experiència
del tub de Kundt, tal com es veu a la figura 1. .
 |
| Fig. 2: El medi el podem representar com un conjunt de partícules
( petites porcions de medi) enllaçades per molles. El moviment
de la pilota test ens informarà del pas d'una ona malgrat que
no puguem veure el medi. |
Podem pensar que, en general, el medi interactua amb les partícules
test en repòs per contacte. Si el medi està en equilibri la interacció
és nul•la. Quan passa una ona, el medi interactua amb les partícules
test.
Aquest model es pot visualitzar força bé si considerem com a medi
la superfície del mar i utilitzem com a partícula test una pilota
de plàstic. En aquest cas, en equilibri, la pilota no només roman
en repòs si estava en repòs, també es pot moure rodolant
per la superfície de l'aigua hi hagi o no onades. Quan no hi ha onades
el medi no altera la trajectòria de la pilota. Quan hi ha onades, la
trajectòria de la pilota és alterada. Així, podem dir que
veiem que passa una ona perquè veiem com la pilota es mou de manera diferent
de quan hi ha equilibri. No ens cal veure l'aigua. No ens cal percebre directament
el medi.
Ones harmòniques
Una altra qüestió de la qual cal una explicació
és: per què donem tanta importància a les ones harmòniques
( sinusoïdals) per sobre d'altra mena d'ones?. Molts dels nostres estudiants
acaben interioritzant que una ona “és” una funció sinusoïdal,
quan, de fet, la forma que tingui l'ona no té per què ser el més
important. O, si és important, cal saber per què. Sota el concepte
d'“ones harmòniques” s'amaga l'equació d'ones. L'equació
d'ones és l'equació que compleix una magnitud física característica
d'un medi sota hipòtesis molt generals, que podrien subscriure tota mena
de medis ( mecànics, electromagnètics, gravitacionals...) per
a petites pertorbacions (linealitat, no dissipació, homogeneïtat
i isotropia). En una dimensió d'espai, l'equació d'ones per a
una magnitud 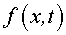 és és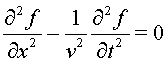 ,
on ,
on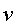 és una constant
característica del medi que s'identifica amb la velocitat de propagació
de l'ona. La solució general d'aquesta equació és és una constant
característica del medi que s'identifica amb la velocitat de propagació
de l'ona. La solució general d'aquesta equació és 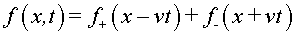 ,
on ,
on 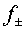 són dues
funcions arbitràries d'un argument. Si, per simplificar, considerem són dues
funcions arbitràries d'un argument. Si, per simplificar, considerem 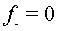 ,
la forma de l'ona la determina la forma de la funció ,
la forma de l'ona la determina la forma de la funció 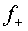 .
L'ona pot tenir qualsevol forma. Un exemple típic és el d'una
sacsejada feta, de manera més o menys caòtica, en una corda. Per
un instant .
L'ona pot tenir qualsevol forma. Un exemple típic és el d'una
sacsejada feta, de manera més o menys caòtica, en una corda. Per
un instant 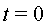 la corda
adoptarà la forma d'un bony, la corda
adoptarà la forma d'un bony, 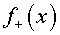 ,
que posteriorment avançarà amb una velocitat conjunta ,
que posteriorment avançarà amb una velocitat conjunta 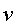 en el sentit positiu de la coordenada
en el sentit positiu de la coordenada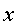 :
: 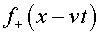 . És il•lustratiu
per als estudiants construir una ona a partir d'una funció relativament
senzilla i localitzada que modeli el bony. Per exemple, partint de la forma . És il•lustratiu
per als estudiants construir una ona a partir d'una funció relativament
senzilla i localitzada que modeli el bony. Per exemple, partint de la forma
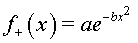 , obtenim l'ona , obtenim l'ona 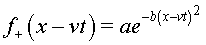 ,
que, fixant alguns valors adequats per ,
que, fixant alguns valors adequats per 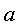 , ,
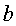 i i 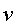 ,
poden representar en un diagrama ,
poden representar en un diagrama 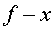 per
a diferents valors de per
a diferents valors de 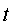 i
comprovar com l'ona efectivament avança. i
comprovar com l'ona efectivament avança.
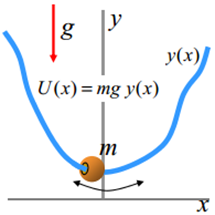 |
| Fig. 3: una partícula es mou per una guia sense fricció
en els si d'un camp gravitatori. |
Un altre exemple és, és evident, la forma inicial
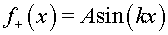 que dóna lloc
a l'ona que dóna lloc
a l'ona 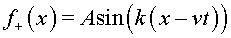 . Diem “és
evidentr” perquè es tracta d'un exemple molt conegut. No ens sembla tan
clar com fer que una corda tingui inicialment aquesta forma, a banda de necessitar
una corda d'una llargada suficient perquè els extrems no afectin l'experiència. . Diem “és
evidentr” perquè es tracta d'un exemple molt conegut. No ens sembla tan
clar com fer que una corda tingui inicialment aquesta forma, a banda de necessitar
una corda d'una llargada suficient perquè els extrems no afectin l'experiència.
Es poden estudiar moltes de les característiques de les ones sense fer
referència a una forma concreta d'ona. En molts casos és més
interessant exemplificar l'efecte a través de la forma  que fer-ho amb ones sinusoïdals, pel fet que la primera és una pertorbació
que en tot instant està localitzada.
que fer-ho amb ones sinusoïdals, pel fet que la primera és una pertorbació
que en tot instant està localitzada.
Tot i això, per què són tan important les ones harmòniques
sinusoïdals? Encara que conceptualment podem donar una forma inicial a
la corda i posteriorment deixar que evolucioni, això no és el
que fem en la pràctica. No és tampoc el que li passa en la natura.
La sacsejada que fem a la corda per donar-li forma inicial gaussiana és
una sacsejada que tenim tota l'estona sota control i aquest control el podem
exercir si la corda no està excessivament tensada. Ni una corda destensada
és un bon model de medi ondulatori ni la natura no es preocupa de tenir
el control de les sacsejades.
Recordem que, abans que passi una ona, ens trobem amb un medi en equilibri.
No sabem com és el medi en general, però sabem que està
en equilibri. Per simplificar ens quedem només amb una partícula
del medi i una dimensió 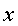 .
La partícula estarà sotmesa a un potencial no conegut, .
La partícula estarà sotmesa a un potencial no conegut, 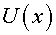 ,
a excepció que sabem que ha de tenir un mínim en la posició
d'equilibri. La situació és completament anàloga al d'una
petita esfera lligada sense fricció a una guia, de forma no coneguda ,
a excepció que sabem que ha de tenir un mínim en la posició
d'equilibri. La situació és completament anàloga al d'una
petita esfera lligada sense fricció a una guia, de forma no coneguda
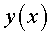 , amb un mínim
en la posició d'equilibri. El potencial en aquest exemple serà
el degut a la gravetat , amb un mínim
en la posició d'equilibri. El potencial en aquest exemple serà
el degut a la gravetat 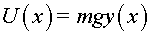 . .
Si desenvolupem el potencial en el primer ordre rellevant no nul i fem servir
que en la posició d'equilibri, que podem situar a 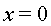 ,
hi ha un mínim , obtenim ,
hi ha un mínim , obtenim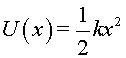 , on
, on 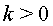 . La conclusió
és que, independentment de la forma concreta del potencial,
en l'exemple de la figura 3 la forma de la guia, la partícula farà
un moviment harmònic al voltant de la posició d'equilibri del
tipus . La conclusió
és que, independentment de la forma concreta del potencial,
en l'exemple de la figura 3 la forma de la guia, la partícula farà
un moviment harmònic al voltant de la posició d'equilibri del
tipus 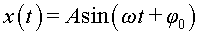 on la freqüència on la freqüència
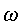 dependrà de dependrà de
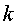 i de la massa de la
partícula. Això vol dir que si separem de l'equilibri qualsevol
partícula d'un medi i la deixem anar el seu moviment serà sinusoïdal. i de la massa de la
partícula. Això vol dir que si separem de l'equilibri qualsevol
partícula d'un medi i la deixem anar el seu moviment serà sinusoïdal.
Com podem fer compatible aquest resultat amb el fet que una ona ha de ser del
tipus 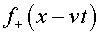 ? Si la pertorbació ? Si la pertorbació
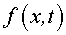 descriu, en l'instant descriu, en l'instant
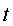 , el desplaçament
de les partícules del medi respecte de les posicions d'equilibri , el desplaçament
de les partícules del medi respecte de les posicions d'equilibri 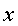 ,
tindrem ,
tindrem 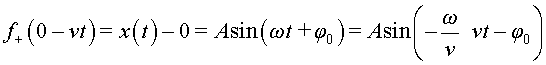 i, per tant, i, per tant,
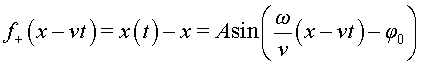 , és a dir,
una ona harmònica. , és a dir,
una ona harmònica.
La conclusió és que les ones harmòniques seran més
fàcilment produïbles a la natura que ones de qualsevol altra forma.
De fet, quan volem detectar el pas d'una ona, sigui mecànica electromagnètica
o gravitacional, el que esperem és que provoquin, en les partícules
test corresponents, moviments harmònics amb una freqüència
característica. Detectar un moviment harmònic de les partícules
test és la prova definitiva que el que ha passat és una ona. El
més difícil és saber quina és la freqüència
esperada de l'ona. En funció d'aquesta freqüència utilitzaríem
un o un altre dispositiu receptor.
Ones electromagnètiques
Quan parlem d'ones electromagnètiques acostumem a dir, bastant a l'inici
de la nostra exposició, que les ones electromagnètiques, com
la llum, són unes ones de camp electromagnètic que es propaguen
en el buit. Aquesta explicació és formalment correcta, si més
no és acceptada com a estàndard, però té una pega.
No incideix en la manera com detectem l'ona electromagnètica, com veiem
l'ona electromagnètica, com veiem la llum?
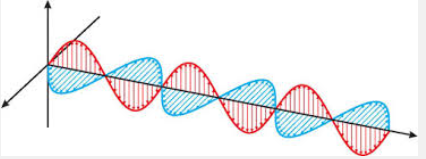 |
| Fig. 4: Típica imatge d'ona electromagnètica. En
vermell el camp elèctric i en blau el magnètic. Com
es mou una càrrega testa causa d'aquesta ona? |
El medi ara queda caracteritzat pel camp electromagnètic. En equilibri,
el camp electromagnètic és nul. Com en el cas mecànic,
el pas d'una ona electromagnètica és l'alteració de l'equilibri
del medi, l'alteració del camp electromagnètic, que deixarà
de ser nul. Quan el medi electromagnètic està en equilibri les
partícules carregades es poden moure lliurement. Quan hi passa l'ona,
la trajectòria de les partícules queda alterada. El model que
podem fer servir per entendre aquest comportament és el de la pilota
test que rodola per la superfície de l'aigua, exposat més amunt.
Els camps electromagnètics interaccionen amb les partícules
carregades. Així, per detectar el pas d'una ona electromagnètica
hem de fer servir partícules carregades. Això és el que
fan les antenes receptores usuals. Quan nosaltres escoltem la ràdio,
passejant pel mig del carrer, és perquè, essencialment, les
partícules carregades de l'antena es posen en moviment pel pas de l'ona
electromagnètica corresponent a l'emissora que volem escoltar. Sintonitzem
l'aparell per tal que afavoreixi el moviment d'aquestes partícules
per l'excitació de freqüència causada per l'ona electromagnètica
de l'emissora que volem escoltar. De tot aquest procés ens n’oblidem
i diem que per detectar una ona electromagnètica ens cal un receptor,
com per exemple una ràdio. Diem que hem detectat l'ona perquè,
a través dels auriculars, escoltem l'ona electromagnètica. Un
procés semblant, però a una escala molt més petita, en
què també hi ha moviment de càrregues que finalment ens
arriben al cervell, és el que fa que veiem directament la llum.
En la descripció d'una ona mecànica no ens cal incidir, no acostumem
a fer-ho, en la interacció entre ona (medi) i partícula test,
perquè el mateix medi proporciona, si més no conceptualment,
partícules (porcions de medi) que, amb certes restriccions (partícules
en repòs), actuen com a partícules test. Si veiem directament
la substància aigua, veurem directament les onades i no ens cal cap
pilota test. Això no vol dir que no hi hagi interacció entre
l'ona i la matèria no pertanyent a l'ona que es pugui trobar al seu
pas.
En la descripció d'una ona electromagnètica fem, crec que, en
part, erròniament, el mateix que amb les ones mecàniques. Ara,
però, no hi ha manera de veure un camp electromagnètic directament.
Persistim, nosaltres i els llibres que ens acompanyen, i identifiquem totalment
l'ona amb el comportament del camp electromagnètic. Fem representacions
més o menys artístiques del camp electromagnètic corresponent
a una ona harmònica (monocromàtica). Aquesta manera de procedir
no és incorrecta i està especialment indicada per a estudiar
amb profunditat les ones electromagnètiques. Però no em sembla
que estigui tan bé quan es tracta d'introduir les ones electromagnètiques.
La figura 4 no ens informa per res de "què fa" una ona electromagnètica.
En aquest sentit és més important incidir en el fet que una
ona electromagnètica posarà en moviment (d'acord amb la força
de Lorentz) les partícules carregades que es trobi al seu pas. Una
ona electromagnètica monocromàtica en el buit es caracteritza,
entre altres coses, pel fet que l'amplitud de camp magnètic és
un factor 1/c l'amplitud
del camp elèctric. Això vol dir que quan l'ona es trobi amb
una partícula carregada, essencialment la farà moure segons
el camp elèctric. Si es tracta d'una ona polaritzada i el camp elèctric
té la direcció, diguem, vertical, la partícula farà
un moviment harmònic vertical tal com faria, en primera aproximació,
una pilota amb les onades del mar.
Ones gravitacionals
En el cas de les ones gravitacionals, el medi queda caracteritzat pel valor
del camp gravitatori . Quan el medi està en equilibri el camp gravitatori
és nul. Quan hi passa una ona gravitacional, els valors del camp gravitatori
queden alterats. Què és una ona gravitacional? Per detectar
el pas d'una ona gravitacional hem d'emprar “càrregues gravitacionals”,
és a dir, masses, partícules amb massa però sense càrrega
elèctrica. També ens cal tenir alguna predicció teòrica
de quines característiques tindrà aquesta ona i, sobretot, saber
com es comportaran les partícules amb massa afectades pel pas de l'ona
gravitacional. És també molt important saber quin és
el rang de freqüències que s'espera que tingui l'ona. Això
ens permetrà dissenyar i dimensionar el detector adequadament.
A la figura 5 es pot veure l'efecte, exageradíssim, que tindria una
ona gravitacional polaritzada plana que incidís en la direcció
normal a la pantalla/paper , sobre un conjunt de petites masses lliures que
abans del pas de l'ona estan en repòs formant un anell circular. De
fet, el possible moviment pot ser la superposició dels dos modes il•lustrats
a les figures. Així, podem dir que una ona gravitacional (harmònica)
és un camp gravitatori oscil•lant que afecta les partícules
amb massa, tal com es veu en aquestes dues figures. Si volem, podem dir més
coses sobre l'espaitemps i la seva curvatura, que tenen la seva importància,
i molta a l’hora de fer la predicció de com són les ones gravitacionals,
què les provoca, etc. Però, si no sabéssim tot això,
l'ona existiria, hi passaria igualment i faria moure l'anell de partícules
com hem esmentat. Com hem comentat a l'editorial d'aquest número, no
cal saber que la llum és una ona electromagnètica per notar-ne
els efectes. El problema és que els efectes d'una ona gravitacional
són molt i molt dèbils. Tot i això, el que no tindria
sentit és pretendre saber "què és" una ona
gravitacional sense conèixer-ne els efectes.
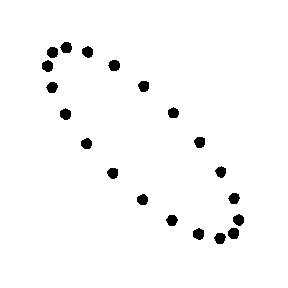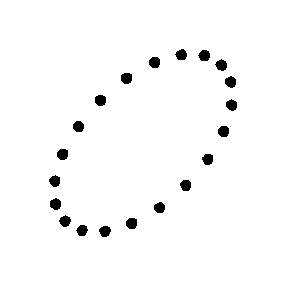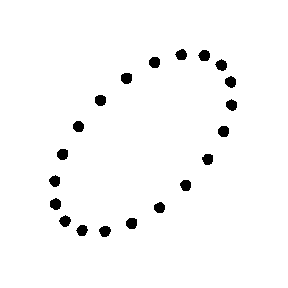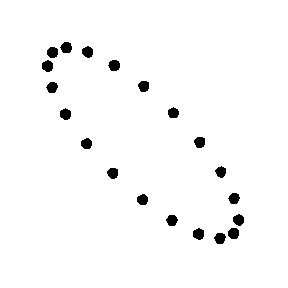 |
 |
| Fig. 5: Moviment d'una anella de petites masses al
pas d'una ona gravitacional en els modes cross i plus. |

|

 8/8
8/8 




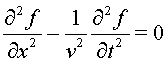 ,
on
,
on
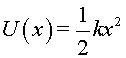 , on
, on 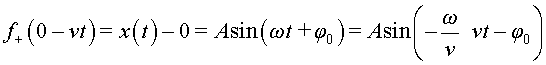 i, per tant,
i, per tant,
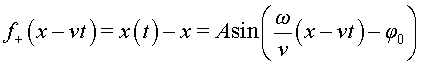 , és a dir,
una ona harmònica.
, és a dir,
una ona harmònica.