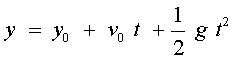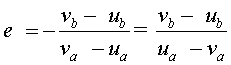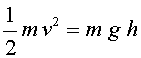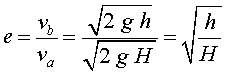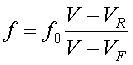núm 18 |
Tardor 2016 |
Societat Catalana de Física |
| Inici |
| Sumari |     5/8  |
 | Experiments de mecànica amb l’ajut del sensor de so dels telèfons mòbils i tauletes Lorenzo Ramírez |
| Es proposa realitzar diferents experiments en el camp de la mecànica aprofitant que els objectes fan soroll en xocar i la tecnologia mòbil pot emetre sons i també gravar-los. |
Guia per al professorat
Orientacions generalsEn el present article es desenvolupen tres experiments de mecànica:
càlcul de g estudiant la caiguda lliure, càlcul del coeficient
de restitució d’una bola en rebotar a terra i mesura de la velocitat
d’un objecte utilitzant l’efecte Doppler. que és capaç d’enregistrar el so i fer-ne una anàlisi posterior.
Aplicació que s'utilitzarà
|
 |
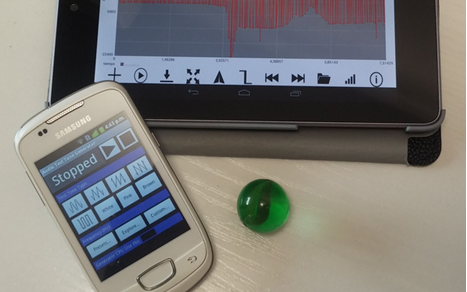
| Fig 2: Aplicació utilitzada |
L’aplicació que s’utilitzarà en els experiments és Mobile Science- AudioTime+ (vegeu la figura 2):
que ha estat realitzada per R. Wisman i K. Forinash, professors d’informàtica
i de física a la Universitat d'Indiana (USA). És una app magnífica
que permet enregistrar l’entrada de so i mesurar temps.
Paral•lelament a la creació d’aplicacions per a tauletes
i telèfons mòbils, Kyle Forinash ha elaborat una sèrie
de propostes experimentals en el camp de la física molt interessants
i traduïdes al castellà, entre les quals es troben les tresque es
proposen en aquest article:
El disseny de l’app està pensat per utilitzar-la en una tauleta
o en un telèfon mòbil gran. En les indicacions als alumnes se
n ’explica el funcionament, però bàsicament la interacció
amb la pantalla és:
En la figura 3 s’indiquen les funcions dels botons de l’aplicació.
- Tocant amb un dit la pantalla es marca una línia. Si es toca en un altre punt de la pantalla es visualitzen els registres en un interval de temps de color groc.
- Si s’arrossega una de les marques es modifica l'interval groc.
- Arrossegant dos dits alhora es pot fer zoom.
- Es pot arrossegar un dit per desplaçar-se cap a l'esquerra i cap a la dreta.
- Si es colpeja dues vegades la pantalla s’eliminen els marcadors de color groc.
 |
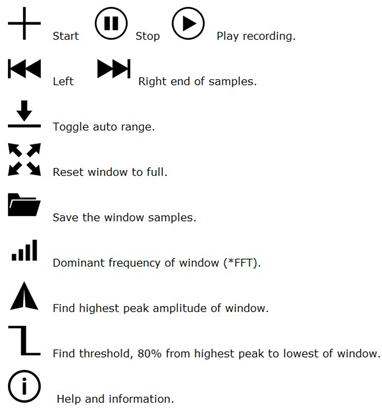| Fig 3: Funcions dels botons d'AudioTime+ |
Atenciól! Aquesta aplicació serveix per gravar so a través del micròfon del dispositiu mòbil. Si es vol utilitzar un micròfon connectat a la sortida dels auriculars per recollir els sons, s’ha d’utilitzar una altra aplicació, bessona d’aquesta: AudioTime (sense el +):
Altres experiments relacionats
La realització d’aquests experiments a les aules
de secundària no és una novetat. La novetat està en les
eines utilitzades i en el fet que l’alumnat disposa d’auestes eines
i pot fer l’experimentació autònomament i a casa seva.
L’estudi de la caiguda lliure i el càlcul de l’acceleració
de la gravetat s’ha fet de moltes maneres. Per exemple, estudiant la caiguda
d’una tanca
que passa davant d’un sensor de llum controlat per l’Exao o el Multilog, i més recentment gravant en vídeo la caiguda de qualsevol objecte
i estudiant posteriorment la gravació amb un programa d’anàlisi de vídeo com el Tracker, de punteig i anàlisi de vídeo, amb el qual podem mesurar temps i altures.
Recentment, Santi Vilchez publicava l’article "Es pot determinar el valor de la gravetat amb una bala?"
en la revista Recursos de física, on descriu com els seus alumnes s’enfronten a aquest problema experimental, primer amb regle i el cronòmetre dels seus telèfons i després amb un dispositiu de mesura basat en Arduino.
També es pot calcular el coeficient de restitució amb un ordinador, un micròfon i el programa Audacity, i si es té la sort de disposar del Multilab i el sensor de distància es pot fer seguint el protocol del CDEC d'energia dissipada en el bot d’una pilota
en què es calcula el coeficient a partir de les successives altures aconseguides per la pilota.
Una altra manera per obtenir les dades és gravar els bots de la pilota en vídeo amb un telèfon (o amb una càmera fotogràfica, o una càmera web, o una videocàmera) i estudiar-los després amb el magnífic programa Tracker. També ens serveix per mesurar temps el programa VLC Media Player.
Quant a l’efecte Doppler, es pot estudiar amb l'esmentat
programa Audacity. Només es necessita un objecte que sigui capaç
d’emetre un to d’una freqüència determinada. Podria
ser un telèfon, però també un altaveu connectat a un altre
ordinador.
A més, l’aplicació que utilitzem en aquest treball, AudioTime+,
es pot usar per fer molts altres d’experiments sobre el so, la dinàmica,
la llum i la termodinàmica, però seguint en el camp de la mecànica,
que és el cas dels exemples desenvolupats, podríem estudiar també:
La caiguda lliure d’un conjunt de cargols enganxats entre si per un fil, bé guardant distàncies iguals o bé distàncies que segueixen una funció quadràtica. Es registra la successió de xocs contra el terra i s’estudia el temps entre cops:
Temporització
Una mitja sessió de classe (uns 20 minuts) per instal•lar
l’aplicació en el dispositiu i conèixer-ne el funcionament.
Una sessió de classe per explicar el fenomen físic i dissenyar
l’experiment.
Una altra sessió per realitzar la presa de dades i analitzar-les, fent
els càlculs, etc. Com que els experiments els realitzarà l’alumnat
amb els seus propis telèfons o tauletes, el poden fer pel seu compte
al centre i/o també a casa seva.
Una tercera per fer l’anàlisi de les dades i exercicis de reforç.
Alumnes als quals s’adreça l’experiència
Alumnat de 4t d’ESO: Càlcul de g per caiguda lliure.
Malgrat que és a 1r de batxillerat que s’aprofundeix una mica en el moviment d’objectes a l’aire amb i sense fregament, ja a 4t d’ESO s’estudia la caiguda lliure simple i es planteja el problema de l’acceleració amb què cauen els cossos.
Alumnat de 1r de batxillerat: Coeficient de restitució
Què seria de la unitat dels xocs sense els xocs inelàstics?
Alumnat de 2n de batxillerat: Mesura de la velocitat d’un objecte utilitzant l’efecte Doppler
Encara que el càlcul de freqüències i velocitats relacionades amb l’efecte Doppler no és matèria de l’examen de selectivitat, és un experiment molt interessant que pot ajudar a entendre els conceptes involucrats en l’efecte.
Alumnat de 4t d’ESO: Càlcul de g per caiguda lliure
Introducció
La caiguda lliure
és la caiguda d'un cos en què únicament
actua el propi pes i no es considera el fregament. Aquest fenomen es produeix
quan els cossos cauen en el buit o quan el fregament amb l'aire gairebé
no els afecta.
En la pràctica, sempre hi ha fregament amb l’aire i empenyiment
d’Arquimedes, però si l’objecte cau a baixa velocitat i és
aerodinàmic i massiu, per exemple una bola d’acer que es deixa
caure des d'una altura de dos metres, la força de fregament és
molt petita en relació amb el pes, així com l’empenyiment,
per la qual cosa es poden negligirr i considerar que el cos està subjecte
només a l’acceleració de la gravetat.
Si l'acceleració és la de la gravetat, tindrà un valor
constant de 9,8 m/s2
i el moviment serà uniformement accelerat (MRUA) i, per tant, es poden
utilitzar les equacions d’aquest moviment.
 |
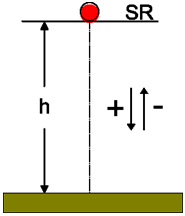| Fig 4: Esquema de la caiguda lliure i el sistema de referència. |
L’equació de la posició del MRUA és:
on y és la posició en qualsevol moment, y0 és la posició inicial, v0 és la velocitat inicial i g és l’acceleració de la gravetat. Si y es mesura en metres (m) i t en segons (s), v es donarà en m/s i g en m/s2.
Les magnituds sempre depenen del sistema de referència. Si es deixa caure una bola des d'una altura h i se situa el sistema de referència en la posició inicial de la bola, es pot usar un conveni de signes que consideri positiu cap avall i negatiu cap amunt, com indica la figura 4. En aquests casos, l’equació de la posició davant el temps, que és la que usarem, serà:
,
ja que la posició inicial és zero, la celeritat
inicial també és zero (parteix del repòs) i la g
és positiva, ja que és cap avall. També es considera el
fregament suficientment petit per negligir-lo.
El que es pretén en aquest experiment és contrastar si el valor
de l’acceleració de la gravetat en el cas real de la bola massiva
que s’ha considerat abans s’apropa al que es reconeix universalment.
Per fer això se substituiran les dades que s’obtindran experimentalment
amb una aplicació per a tauletes i telèfons mòbils anomenada
AudioTime+,
en l’equació de la posició en funció
del temps que s’ha obtingut abans. Per aconseguir les dades s’ha
d’aprendre a utilitzar l’aplicació i enregistrar sons i analitzar-los.
Material
Una boleta d’acer (o de vidre o de...).
Realització/procediment
S’enganxa amb cinta adhesiva la bola a un fil de cosir
i es penja d'un suport a una altura determinada del terra, per exemple a un
metre. En un moment determinat es talla el fil amb les tisores amb un cop sec
mentre es graven els sorolls que fan les tisores i el soroll "clonc"
de la bola contra el terra. Si s’ha mesurat l’altura i ara es mira
el temps entre els dos sorolls enregistrats ja es pot calcular l’acceleració
de la gravetat. A continuació ho detallem.
Es penja la bola d’un fil en un suport que permeti que la bola pugui caure
lliurement al terra i es mesura acuradament l’altura a la qual queda.
La mesura rigorosa de l’altura és fonamental, ja que és
la magnitud en la qual es pot cometre l’error més gran. Aquí
els alumnes poden mostrar l’enginy que tenen dissenyant diversos muntatges.
S’encén el dispositiu mòbil i s’obre l’aplicació
AudioTime+. Es posa la tauleta o telèfon a l’alçada de la
meitat del recorregut de la bola, però sense que en dificulti la caiguda,
i s’inicia la gravació prement el botó inici +
de l'aplicació.
 |
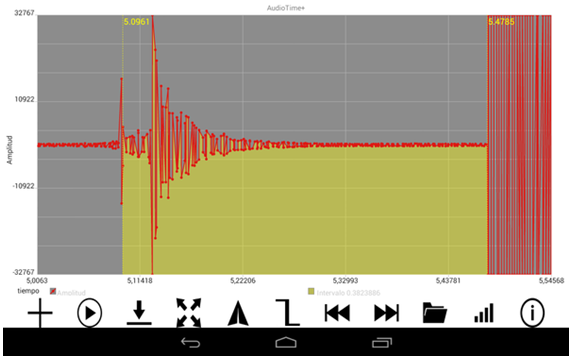| Fig 5: Selecció temporal entre el so inicial de les tisores i so final del xoc. |
Ara és el moment de tallar el fil amb unes tisores amb un cop sec, procurant
fer soroll, i una vegada que la bola ha xocat amb el terra s’atura l’app
amb el botó pausa, 
.
Tocant la pantalla amb dos dits s’amplia la imatge fins que es vegin bé
els dos sorolls, i es prem l’inici del so "clic" de les tisores
i es torna a prémer la pantalla a l’inici del soroll "cloc"
de la bola. Apareixerà una banda groga entre els dos punts, tal com mostra
la figura 5.
En la pantalla es veu el temps inicial i el final, en segons i amb quatre decimals,
i el valor de l’interval amb set decimals, que és el temps que
la bola ha trigat a caure, en aquest cas a una altura de 73,6
cm.
Si es vol, es pot guardar la gravació prement el botó de la carpeta
i donant-li un nom. Es guarda en la carpeta Audiotime+.
Es pot repetir l’experiment i/o demanar els resultats a altres equips
de la classe per aconseguir mitja dotzena de mesures.
Activitats
Activitat 1: S’Introdueix el valor de l’altura i del temps de caiguda en l’equació de la caiguda lliure i es calcula l’acceleració de la gravetat g.
Activitat 2: Després de repetir l’operació amb totes les mesures, es calcula el valor més probable de g com mitjana aritmètica dels valors obtinguts i es compara amb el que se suposa que hauria de sortir.
Activitat 3: Encara que no es calculi la incertesa en la mesura, s’hauria d’analitzar perquè l’error en l’obtenció de g és determinat sobretot per la mesura de l’altura des d'on es deixa caure la bola.
Activitat 4: Per què s’ha de situar la tauleta o el mòbil a l’alçada de la meitat del recorregut de la bola?
Alumnat de 1r de batxillerat: Coeficient de restitució
Introducció
L’estudi dels xocs forma part dels continguts de la física de 1r curs de batxillerat i en molts casos se'n proposa l'estudi experimental. Per exemple, en la unitat destinada a l’estudi dels transports del llibre interactiu Física en Context, en el punt 3, "Una nova mirada als xocs",
hi ha l’activitat 7: Energia dissipada en el bot d’una pilota, en la qual es demana que s’estudiï la pèrdua d’energia en els xocs i es proposa un protocol
que guia en la mesura amb un sensor de distància de
les altures que aconsegueix una pilota de bàsquet en rebotar.
El que se us proposa en aquesta experiència és aprofundir en l’estudi
dels xocs introduint un nou concepte, el coeficient de restitució, i
obtenir les dades per calcular-lo mitjançant mesures de temps amb el
sensor de so de la vostra tauleta o telèfon mòbil. Per fer això
s’ha d’aprendre a utilitzar l’aplicació AudioTime+
enregistrar sons i analitzar-los.
Material
Una bala (o una pilota o un baló...)
El coeficient de restitució en el xoc
En qualsevol xoc, els cossos experimenten una deformació i s'alliberen petites quantitats d’energia en forma de calor, però si considerem el cas ideal de la col•lisió, perfectament elàstica, entre dos objectes de masses, m1 i m2, que es mouen en la mateixa direcció, l'energia i la quantitat de moviment totals es conserven, és a dir, l’equació de la conservació de l’energia cinètica en el xoc és:
,
on va i vb són les celeritats del l’objecte 1 abans i després del xoc, i ua i ub són les de la massa 2 també abans i després.
L’equació de la conservació de la quantitat de moviment en el xoc és:
.
Si es combinen linealment les dues equacions s’obté aquesta:
que també es pot escriure
La fórmula anterior implica que, en el cas ideal d'un
xoc perfectament elàstic en una direcció, la velocitat relativa
abans de xocar, 
, és
igual a la velocitat relativa després del xoc canviada de signe, 
.
Però si en el xoc hi ha pèrdues energètiques (és
a dir, sempre), la velocitat relativa després del xoc és més
petita i l’equació es pot escriure:
on e és un coeficient, anomenat de restitució, que mesura indirectament la proporció d’energia perduda en el xoc:
En analitzar aquesta equació es poden fer les consideracions següents:
1. Si el xoc és completament elàstic, les velocitats relatives abans i després són iguals i el coeficient de restitució és igual a 1, e = 1.
2. Si el xoc és totalment inelàstic, els dos cossos continuen junts després del xoc (mateixa celeritat),
, i el coeficient de restitució és igual a 0, e = 0.
3. En la resta de casos, e és un nombre entre zero (0) i u (1).
 |
| Fig 6: Esquema del rebot d'una pilota per calcular el coeficient de restitució. |
A més, si un dels cossos que xoquen és tan massiu que, estant inicialment quiet respecte al sistema de referència que considerem, després del xoc no es mou, la seva celeritat és sempre zero i l’equació del coeficient de restitució queda en aquest cas:
.
És a dir, que e
solament depèn de les celeritats del propi cos, al qual es pot atribuir
aquest valor de e com a propietat seva. Així, el coeficient de restitució
(e) per
a un material es defineix com la relació de la velocitat d'un objecte
d’aquest material abans i després d'una col•lisió
amb una superfície dura.
En el dibuix del costat (vegeu la figura 6) es representa una pilota que es
deixa caure des d'una altura, H,
rebota amb el terra i arriba una altra vegada fins a una altura menor, h.
S’utilitzi el conveni de signes que sigui, sempre les velocitats de la
pilota abans i després del xoc tindran signes contraris; per tant:
.
Com hem argumentat abans, si la col•lisió és
perfectament elàstica, és a dir, si es conserva l’energia
en el xoc, les dues velocitats tindran el mateix mòdul i e
= 1., i si el xoc és perfectament inelàstic, és
a dir, si l'objecte s'enganxa a la superfície després de la col•lisió,
el e = 0.
El coeficient de restitució (e),
doncs, es pot determinar pel rebot de l'objecte del material que es vol estudiar
sobre una superfície dura.
Les pilotes de golf solen tenir un e
= 0,78; les pilotes de bàsquet tenen un e
entre 0,81 i
0,85, i les pilotes de tennis tenen un e
entre 0,89 i
0,91. Les boletes de vidre poden tenir un e
de fins a 0,95
(sempre que no es deformin i/o es trenquin amb l'impacte). El coeficient de
restitució d'altres objectes com raquetes de tennis i pals de golf es
pot determinar pel rebot d'una esfera dura a sobre. Així, les raquetes
de tennis tenen un e
d'aproximadament 0,85
i els pals de golf de 0,83.
Mesurar directament la velocitat de les pilotes abans i després de botar
és molt complicat. Més fàcil és calcular el coeficient
de restitució a partir del temps entre rebots o a partir de la determinació
de l’altura H
des de la qual es deixa caure l’objecte i l'altura h
a la qual arriba en rebotar. Veiem en aquests casos com és l’equació
que permet calcular el coeficient de restitució.
 |
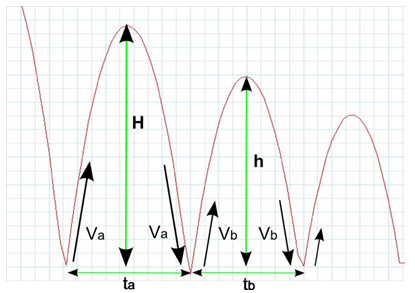| Fig 7: Rebots d'una pilota sobre una superfície dura. |
En el diagrama de dalt (figura 7), que representa la posició en funció del temps d’una pilota que va botant i rebotant sobre una superfície dura, va és la velocitat després del primer bot, vb és la velocitat després del segon bot, H és l'altura del primer bot i h és l'altura del segon bot. Si negligim la resistència de l'aire, va és també la velocitat de la pilota just abans del segon bot. El primer rebot triga un temps ta i el segon rebot triga un temps tb.
Com que el moviment de caiguda de la pilota és el de caiguda lliure, es pot calcular la celeritat en el moment de l’impacte amb el terra a partir de l’equació v=g t, on t és el temps de caiguda de la pilota des del punt més alt de la trajectòria, és a dir, la meitat del temps entre xoc i xoc. Per calcular el coeficient de restitució en funció del temps n'hi ha prou a fer el quocient entre dos temps successius:
Si es vol calcular la celeritat de la pilota just abans del xoc en funció de l’altura, s’ha d’utilitzar una altra equació del moviment uniformement accelerat, o bé el principi de conservació de l’energia mecànica: l’energia potencial a dalt de tot serà igual a l’energia cinètica a baix:
Aïllant la velocitat va, que és la velocitat final que adquireix la pilota en caiguda lliure des de l'altura H es té:
I per a vb:
El coeficient de restitució en funció de l’altura serà:
Realització/procediment
Mesurarem el coeficient de restitució (e) del xoc d’una bala al terra de la classe en funció del temps entre els bots. Per això, deixarem caure la bala des d’una altura qualsevol i gravarem amb l’aplicació AudioTime+ els sorolls que fa en rebotar contra el terra. Després mesurarem el temps entre dos xocs successius i calcularem el coeficient.
 |
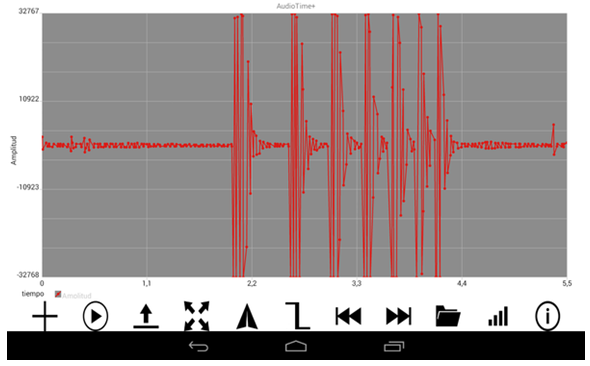| Fig 8: Gravació dels rebots d'una bala amb el terra. |
S’inicia l’app AudioTime+ i es prem el botó
inici (+) per començar a gravar. Es deixa caure
la bala i que reboti diverses vegades. A continuació s’atura l'enregistrament
prement el botó parar 
.
Apareixerà una gràfica com la de la figura 8 en la qual es veuen
les pertorbacions sonores produïdes pels successius xocs al terra de la
bala. S’han de marcar en la pantalla dos moments successius en els quals
s’inicia el soroll del xoc. Això es pot fer de dues maneres:
1. Es prem amb el dit en el dos punts que es consideri. Si es produeix una equivocació, es pot moure la posició arrossegant la marca amb el dit. Si els senyals estan junts, prèviament es poden separar/ampliar separant els dos dits a la pantalla.2. Si es prem el botó
es col•locarà una línia en el primer bot, el que té el senyal més fort, en la part més alta del senyal. Si es veuen en pantalla diversos rebots, s’han d’ampliar els senyals utilitzant dos dits fins que només siguin visibles dos xocs a la pantalla. A continuació es torna a prémer el botó
En qualsevol dels dos casos, apareix el valor del temps (vegeu
la figura 9) entre els dos senyals a la part inferior dreta de la pantalla.
A aquest temps li direm ta.
Per tornar a veure tot el que hem gravat s’ha de pitjar el botó
amb quatre fletxes . Si ara es fa un doble toc a la pantalla eliminarem les
dues línies grogues de la primera mesura. Es poden repetir els passos
d’abans per trobar el temps entre el segon i el tercer rebot. Aquest nou
temps és tb.
A continuació es pot seguir el procés amb tc,
td...
Ara ja es pot trobar el coeficient de restitució dividint el temps segon
pel primer: e=tb/ta.
Si es vol, es pot guardar la gravació prement el botó de la carpeta
i donant-li un nom. Es guarda en la carpeta Audiotime+.
 |
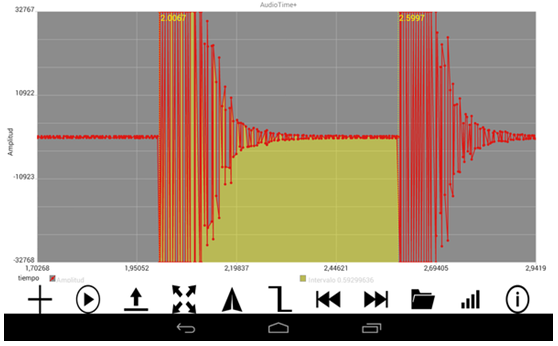| Fig 9: Captura de pantalla d'AudioTime+ que mostra l'interval entre el primer i el segon bot |
Activitats
Activitat 1: S’ha d'omplir una taula amb els valors de temps recollits i calcular el valor del coeficient de restitució per a cada parell de dades.
Activitat 2: En analitzar els valors obtinguts, estan tots dins el mateix rang? Es produeix un salt en els valors a partir d’un determinat rebot? Si els valors dels coeficients en cada bot estan dins el mateix rang, es pot calcular el valor més probable i la seva incertesa?
Activitat 3: Altres grups de la classe han obtingut resultats similars? És el resultat esperat?
Alumnat de 2n de batxillerat: Mesura de la velocitat d’un objecte utilitzant l’efecte Doppler
Introducció
L’efecte Doppler,
o també efecte Doppler-Fizeau, consisteix en la diferència
entre la freqüència emesa per una font d'una ona sonora (es pot
produir amb qualsevol tipus d’ona, però aquí no és
el cas) i la freqüència que percep un observador, a causa del moviment
relatiu entre la font i l’observador. L’efecte es produeix tant
si és la font sonora que es mou com si és el receptor o com si
són tots dos els que es mouen.
L’efecte produeix un augment cap a més agut (freqüència
més gran) del to emès per la font en repòs en aproximar-se
la font a l’observador i una disminució cap a més greu (freqüència
més petita) en allunyar-se'n. En la figura 10 veiem representat el canvi
de freqüència de la sirena d’un cotxe segons s’apropa
o s’allunya al micròfon.
 |
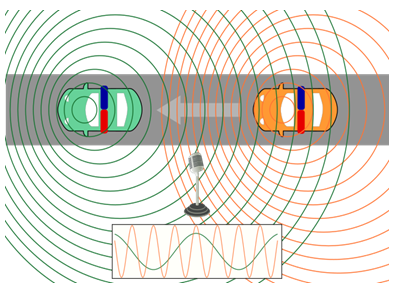| Fig 10: Efecte Doppler en apropar-se o allunyar-se. |
Aquesta variació es pot calcular a partir de la següent expressió que lliga les freqüències i les velocitats relatives entre la font sonora i el receptor:
on f
és la freqüència que percep el receptor, f0
és la freqüència que emet la font, v és la rapidesa
de propagació de l’ona sonora, VR
és la celeritat del receptor i VF
és la rapidesa de la font de so.
Si el receptor està quiet i la font s’apropa es pot aïllar
la celeritat de la font en funció de les freqüències, i l’equació
quedarà:
que és la fórmula que s’utilitzarà
en els càlculs que es faran en aquest experiment.
L’estudi de l’efecte Doppler forma part dels continguts de la física
de 2n curs de batxillerat i en molts casos se'n mostren exemples qualitatius,
com ara enganxar un brunzidor a una corda i fer-lo girar per damunt del cap
i sentir com va canviant el so que es percep, o veure un vídeo en el
qual apareix l'efecte Doppler. Així, en la unitat destinada a l’estudi
de la música i el so del llibre interactiu Física en Context,
de 2n batxillerat, en el punt 1.3.4, Efecte Doppler,
s'hi mostra un vídeo de Carl Sagan que il•lustra l’efecte
També es pot estudiar quantitativament l’efecte amb simulacions com les que conté la pàgina "Efecto Doppler acústico",
del llibre digital Física, del professor Ángel Franco.
El que es proposa, però, en aquesta activitat quantitativa és aprofundir en la comprensió de l’efecte Doppler mesurant experimentalment el canvi de freqüència que es produeix quan un objecte que emet un so s’apropa o s'allunya d’un receptor i calculant la velocitat que porta. Per poder-ho fer s’ha d’aprendre a utilitzar l’aplicació AudioTime+ i a enregistrar sons i analitzar-los.
 |
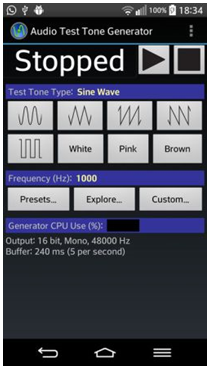| Fig 11: App Audio Test Tone Generator |
Material
Dos dispositius mòbils (tauleta o telèfon mòbil).
Realització/procediment
Es tracta de recollir en una tauleta o telèfon mòbil,
que estigui en repòs, el to que emet un altre aparell que inicialment
està parat i després s’apropa al primer. A continuació,
a partir de la gravació, cal mesurar les freqüències en les
dues situacions.
Es comença posant sobre una taula l'aparell amb AudioTime+ i obrint l’app.
En el segon dispositiu s’obre l’aplicació Audio Test Tone
Generator, se selecciona ona sinusoïdal, una freqüència en
presintonies (per exemple, 1000
Hz) i es prem el play (vegeu la figura 11).
Se subjecta amb la mà l’aparell que està emetent el so a
una distància aproximada d’un metre de l’altre dispositiu.
És el moment d’iniciar en la tauleta quieta la gravació
del to amb l’app AudioTime+ prement el botó d’inici
(+) i deixar que gravi uns moments el so sense cap moviment,
és a dir, el to amb la freqüència que realment emet la font.
Passats un parell de segons s’ha d’apropar el telèfon sonor
al més ràpidament possible a l’aparell receptor. A continuació
ja es pot aturar la gravació prement el mateix botó del principi.
Sortirà una imatge semblant a la figura 12.
 |
| Fig 12: Captura del so emès en repòs i en moviment |
Es pot guardar la gravació prement el botó carpeta
si es vol tornar a analitzar-la amb un altre programa. S’hi ha de donar
un nom i guardar-lo en la carpeta Audiotime+ de l’arrel del telèfon.
En al pantalla d’AudioTime+ ampliarem amb dos dits un petit interval de
temps inicial, quan encara el telèfon no es movia, i premem el botó
TTF . Apareixerà una pantalla com la de sota en la qual es pot veure
l’interval de temps analitzat i quatre freqüències fonamentals
trobades; se n'’haurà de calcular la mitjana per obtenir el valor
més probable de la freqüència mesurada (vegeu la figura 13).
L’anàlisi TTF que fa la màquina és una anàlisi
de Fourier
Simplificant molt: l’aplicació descompon el senyal sonor en un conjunt de senyals sinusoïdals (harmònics). La freqüència més petita correspon a l'harmònic fonamental i és la que caracteritza el senyal emès; les altres caracteritzen el timbre del so.
Algunes vegades algun dels quatre valors duplica o quadruplica
la freqüència fonamental, i s’ha d’obviar. En tot cas,
es pot tornar a seleccionar un altre bocí de la gravació en la
mateixa zona i tornar a obtenir la freqüència.
tenció! Per seleccionar i fer l’anàlisi TTF només
s’ha d’ampliar el bocí que es vol analitzar, no s’ha
d’usar la franja groga que apareix entre dues marques quan es toca la
pantalla dues vegades amb un dit.
 |
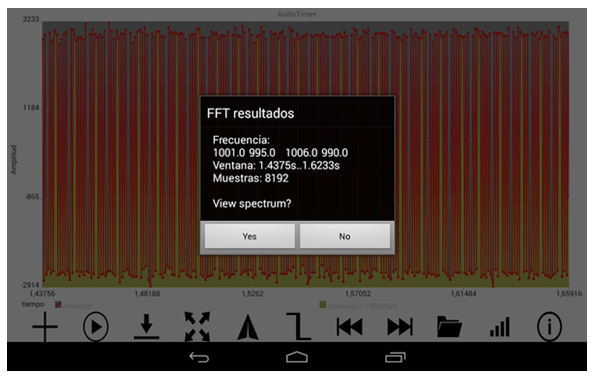| Fig 13: Freqüència de l'harmònic fonamental
(4 valors) |
Una vegada s'ha obtingut la freqüència que emet la font, s’ha
de seleccionar una part de la gravació on el telèfon mòbil
s’hagi mogut. La part en la qual l’amplitud de l’ona sonora
creix indica que els aparells s’apropen i, per tant, que hi ha moviment.
S’ha de tornar a fer l’anàlisi de Fourier per a aquesta part
i obtenir el valor de la nova freqüència.
Activitats
Activitat 1: Com és el valor de la freqüència que es mesura quan hi ha moviment? És com s’havia previst? Els altres grups de la classe tenen resultats semblants?
Activitat 2: Amb els valors de les freqüències es pot calcular la celeritat a la qual s’ha mogut el mòbil? Quin grup de la classe ha tingut més empenta?
Activitat 3: Per què es proposa en les instruccions que s’ha d’apropar el telèfon sonor al més ràpidament possible a l’aparell receptor?
Activitat 4: Què és el que indiquen aquells valors que de vegades troba l’analitzador TTF que dupliquen o quadrupliquen la freqüència fonamental?
Guia per al professorat
Comentaris a les activitats
Alumnat de 4t d’ESO: Càlcul de g per caiguda lliure
Activitats 1 i 2: Com que l’experimentació és molt ràpida de fer, és fàcil repetir-la vàries vegades. En tot cas, el contrast d’estratègies, dissenys experimentals i resultats entre els grups de la classe és fonamental.
Activitat 3: Considero que a 4t d’ESO no cal fer càlculs d’incerteses, però si que cal reflexionar al respecte. Un bon manual d'aquest tema per al batxillerat es por veure a Errors en les mesures
Activitat 4: Encara que la velocitat del so és prou gran en comparació de la de caiguda de la bola, no està de més fer que els temps que tarden els dos sons en arribar al mòbil o tauleta siguin el mateix.
Alumnat de 1r de batxillerat: Coeficient de restitució
Activitat 1: Com que l’experimentació és molt ràpida de fer, és fàcil repetir-la vàries vegades, encara que prendre les dades de cada experiment és més lent. En tot cas, els diversos grups de la classe poden compartir el resultats. També poden repetir l’experiment amb una bola d’un altre material per estudiar si els resultats són equiparables.
Activitat 2: Depenent del material de la
bola que es deixa caure es pot trobar que el valor del coeficient de restitució
sigui pràcticament igual des del primer bot, com en una pilota de basquet,
però hi ha altres materials, com el d’algunes bales de vidre, que
en els primers bots es deformen molt més que en els següents quan
el xoc és menys violent, i això no ho fan gradualment sinó
patint un canvi brusc del valor del coeficient a partir d’un bot determinat.
Un manual per estudiar com calcular la incertesa en les mesures experimentals
es pot baixar de Errors en les mesures
Alumnat de 2n de batxillerat: Mesura de la velocitat d’un objecte utilitzant l’efecte Doppler
Activitat 1: La freqüència ha de ser més gran, ja que els aparells s’apropen.
Activitat 2: No cal tornar a repetir l’experiment,
més enllà de tornar a comprovar que la freqüència
augmenta en apropar els aparells. L'experiment és irrepetible perquè
encara que sigui la mateixa persona la que mogui el telèfon és
molt difícil que ho torni a fer de la mateixa manera.
Una altra qüestió és tornar realitzar l’experiment
però d’una manera diferent. Per exemple: en lloc d’apropar
la font de so es pot allunyar o en lloc de moure l’emissor es por moure
el receptor i d’aquesta manera comprovar l’efecte Doppler en diferents
situacions.
Activitat 3: Quant més gran és la celeritat més canvia la freqüència i més es nota la diferència.
Activitat 4: Els harmònics múltiples de la freqüència fonamental.
