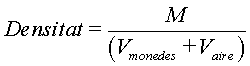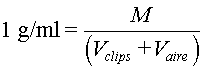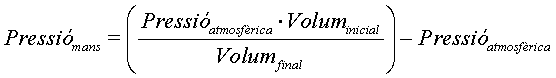Orientacions per al professorat
Construcció
El dimoniet de Descartes se sol presentar com un petit
truc de màgia en el qual es fica un petit objecte (el dimoniet)
dintre d'una ampolla de plàstic plena d'aigua. El mag fa veure que quan
li diu: "baixa", el dimoniet baixarà, i si li diu
que pugi, el dimoniet obeirà. El truc consisteix a agafar l'ampolla amb
una mà i, amb aquesta, fer-hi pressió per tal d'alterar-ne l'estat
de flotabilitat.
Per poder construir un dimoniet necessitarem:
- Poder afegir aire de tal manera que es pugui comprimir.
- Poder calcular el volum i la massa total del dimoniet.
L'aire el podem afegir amb una xeringa.
El volum d'aire afegit el podem conèixer gràcies
a la xeringa la qual ha d'estar graduada. El volum de les monedes es pot calcular
fent servir un peu de rei; si cal, però, a Internet se'n poden consultar
les característiques.
La massa la podem conèixer de diferents maneres:
- Si són monedes, podem buscar-ne les característiques per
Internet.
- Podem mesurar-ne la massa amb una balança.
Temporització
Alumnes als quals s’adreça l’experiència
- El nivell més adient al qual s'adreça aquesta activitat
seria 4t de l'ESO. No obstant això, també la poden realitzar
l'alumnat si ja coneix els conceptes de pressió i densitat, principi
de Pascal i, també, el principi d'Arquimedes.
Metodologia
- Resolució d'un problema en el laboratori amb preguntes guia.
La gestió de la classe podria ser la següent. El professorat
mostra un exemple del dimoniet i reparteix el guió de la classe.
En grups, l'alumnat ha de contestar en el full i construir el seu propi
dimoniet. El professorat dóna suport als grups i en revisa les respostes
en el full de cada grup durant la classe.
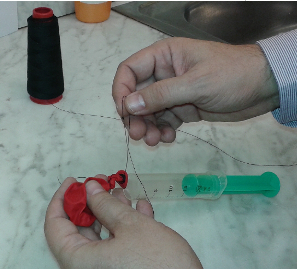 |
| Fig. 1: Cordant
el globus. |
Orientacions tècniques
- Es pot fer amb material casolà; això no obstant, es pot
fer servir una balança amb una precisió de 0,1
g.
- Si es guarda algun projecte acabat com a mostra, amb el temps pot succeir
que l'aigua agafi un color rogenc. Això es pot fer servir per plantejar
un problema i emetre'n hipòtesis. Aquest color pot ser produït
per oxidació. Si s'has fet servir elements de ferro, l'aire reacciona
amb el ferro dóna òxid de ferro.
- L'altre efecte que també es pot observar amb el temps és
que el dimoniet s'enfonsa. La causa és la mateixa que en el cas
anterior. L'oxidació del ferro fa que el volum de l'aire contingut
en el dimoniet minvi.
- La massa i el volum del globus sense aire es pot considerar negligible
- Si l'ampolla té la boca petita, és difícil ficar-hi
el globet dins. Això es pot resoldre tenint en compte el següent:
- L'aire ocupa volum. Necessitarem col·locar una canyeta
de beure sucs entre la boca de l'ampolla i el globus, d'aquesta
manera l'aire podrà sortir de l'ampolla en el moment d'introduir-hi
el globet.
- La fricció. La goma fa fregament amb la boca de l'ampolla,
cosa que es pot reduir si es fa servir aigua amb sabó.
- Hi haurà dificultats per ficar la boca del globet en la sortida
de la xeringa. Per facilitar aquest fet es recomana ajudar-s'hi fent servir
un fil de cosir abans d'injectar l'aire.

 
Full de l’alumnat
Objectiu
El problema consisteix a construir un dimoniet de Descartes
fent mesures i càlculs. Prèviament se n'haurà de fer una
descripció acurada del funcionament.
 |
| Fig. 2: Fent
pressió sobre l'ampolla. |
Introducció
Per poder resoldre el problema s'han de recordar els conceptes
següents:
Un cos submergit en un fluid surarà o s'enfonsarà
en funció de la seva densitat respecte a la del fluid. Si el cos té
més densitat, s'enfonsarà; en cas contrari, surarà.
La densitat mitjana d'un cos es pot calcular dividint-ne la massa pel volum.
El principi de Pascal. La pressió exercida en un punt d'un fluid incompressible
es transmet a tots els punts del fluid.
Llei de Boyle-Mariotte. En un gas ideal a temperatura constant, la pressió
i el volum són inversament proporcionals.
El principi d'Arquimedes. Un cos submergit en un fluid experimenta una empenta
cap amunt igual al pes de la massa del fluid que ocupa.
 |
| Fig. 3:
Material |
Materials i eines
- Xeringa graduada.
- Ampolla de plàstic amb tap que tanqui hermèticament.
- Globets.
- Monedes de cèntim, clips, cargols o sorra de platja neta.
- Aigua de l'aixeta.
- Balança i/o peu de rei.
Realització
Activitat 1: Descriure qualitativament el
funcionament del dimoniet de Descartes.
A partir dels conceptes teòrics comentats abans i de les pistes següents,
expliqueu el funcionament de l'experiència.
Surant:
si pressió 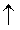 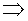 volum volum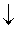 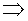 densitat
densitat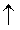 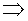 (si densitat >1)
(si densitat >1)
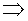  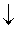 |
Enfonsat: si pressió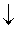 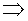 volum
volum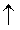 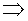 densitat
densitat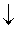 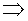 (si densitat <1)
(si densitat <1)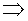
 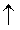 . . |
Activitat 2: Calcular, mesurar, construir i comprovar el dimoniet
de Descartes.
Podeu seguir les preguntes guia següents:
- Quina densitat ha de tenir el globet perquè inicialment suri?
- Quina densitat ha de tenir el globet perquè estigui a punt d'enfonsar-se?
- Defineix una densitat. Serà una hipòtesi, ja que només
sabràs si serà encertada quan ho comprovis.
- Fixa un valor de volum. Considera el criteri següent: com més
gran és la mesura, més petit serà l'error relatiu
de la mesura.
- A partir del volum i la densitat hauràs de fixar un valor de
massa orientativa.
- Quan tinguis clar el volum que vols que tingui i la massa que hi has
de posar, ja pots construir el dimoniet i comprovar-ne el funcionament.
Activitat 3 (Opció 1): Busquem els
límits. (no es disposa de cap balança)
- Construeix un dimoniet com el de l'activitat (2) i fes-lo funcionar.
- Ara treu-li una moneda i fes-lo funcionar. Observaràs que cal
estrènyer l'ampolla amb més força que abans.
- Ara ves traient dues, tres, quatre, cinc... monedes. Veuràs
que cada cop costa més d'enfonsar. On és el límit?
És a dir, quin és el número de monedes més
petit que ha de tenir el dimoniet per poder-lo enfonsar?
- Calcula el pes d’aquest darrer dimoniet i el seu volum d’aire en el
moment que comença a enfonsar-se (
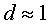 ). ).
- Amb els volums inicial i final d’aire, i considerant que la pressió
abans d'estrènyer l'ampolla és
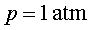 ,
calcula la pressió que suporta el dimoniet quan s'enfonsa (has
d'aplicar la llei de Boyle). ,
calcula la pressió que suporta el dimoniet quan s'enfonsa (has
d'aplicar la llei de Boyle).
- L'augment de pressió l'has fet amb les teves mans. Així
doncs, quina és la màxima pressió que pots fer amb
les mans per estrènyer l'ampolla?
Activitat 3 (Opció 2): Busquem els
límits. (es disposa d'una balança)
En un globus amb 20
ml d'aire, hi penjarem clips. Triarem el nombre de clips (n)
de la mateixa manera que a l'activitat (2). Anirem provant d'enfonsar-lo cada
vegada amb menys clips. L'últim intent serà quan una mateixa persona
ja no pugui fer que baixi al fons.
Podem emplenar lat taula següen:
Nombre de clips |
n
|
n-1
|
n-2
|
... |
massa (g)
|
|
|
|
|
Volum en el límit de funcionament
(ml) |
|
|
|
|
Pressió amb les mans. (atm) |
|
|
|
|
En aquest cas, el volum dels clips es pot calcular tenint en
compte que acostumen a estar fets de ferro.
Fes un comentari de la taula i, indica quina seria la pressió
màxima que pots exercir amb les mans sobre l'ampolla.
Activitat 4: Si t'ha sobrat temps, posa una
mica d'imaginació i intenta fer un esbós d'un dispositiu per mesurar
la pressió a l'interior d'una ampolla amb un líquid (manòmetre).
Anàlisi i tractament de les dades
Es pot considerar com a hipòtesi de treball negligible
la massa i el volum del globet. El volum del globet és pot calcular així
com la suma de l'aire injectat amb el volum de les monedes introduïdes.
També és pot negligir la massa de l'aire enfront a la de les monedes.
Llavors, la densitat del dimoniet serà:
on M
és la massa de les monedes. 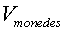
i 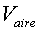 són el
volum de les monedes i de l'aire respectivament.
Per al càlcul del volum d'enfonsament s'ha de considerar que la densitat
és aproximadament 1
g/ml. De l'equació anterior obtindrem el volum d'aire a l'inici,
és a dir, quan no fem una pressió extra amb les mans. El volum d'aire en el moment de l'enfonsament serà:
La pressió d'enfonsament la podrem obtenir a partir
la llei dels gasos, quan la temperatura és constant:
La pressió amb les mans serà la pressió
d'enfonsament menys la pressió atmosfèrica, la qual també
serà la pressió inicial.
Si aïllem la pressió amb les mans:
on el volum final serà l'obtingut amb l'equació (3).

 
Solucions
Activitat 1: Descriure qualitativament el
funcionament del dimoniet de Descartes.
El globet sura. Quan començo
a fer pressió amb la mà, la pressió es transmet al
dimoniet pel principi de Pascal. L'aire dintre del dimoniet experimentarà
un augment de la pressió i per la llei de Boyle-Mariotte, el volum
minvarà. Com que la densitat és la massa dividida pel volum,
com menys volum més densitat; com a conseqüència, la
densitat anirà augmentant fins que superi la densitat de l'aigua.
En aquest cas, el dimoniet baixarà.
El globet està en el fons.
Això és per la causa de tenir més densitat que l'aigua.
Si començo a afluixar amb la mà, la pressió disminuirà
en el fluid. Pel principi de Pascal, la pressió es transmet al globet
amb la qual cosa la pressió també disminuirà en l'aire
del dimoniet. Per la llei de Boyle-Mariotte, quan baixa la pressió
el volum del gas augmentarà. Al variar el volum, la densitat del
globet també canviarà, de fet, com que el volum augmenta,
llavors la densitat disminueix. En el moment que la densitat sigui inferior
a la de l'aigua, el dimoniet començarà a pujar.
Activitat 2: Calcular, mesurar, construir i comprovar el dimoniet
de Descartes.
Preguntes guia:
- Quina densitat ha de tenir el globet perquè inicialment suri?
-
La densitat del globet ha de
ser inferior a 1
g/cm3.
-
Quina densitat ha de tenir el globet perquè
estigui a punt d'enfonsar-se?
La densitat ha de ser pròxima
a 1 g/cm3.
-
Defineix una densitat. Serà una hipòtesi,
ja que només sabràs si serà encertada quan ho comprovis.
Per exemple 0,9
g/cm3 .
-
Fixa un valor de volum. Considera el criteri següent:
com més gran és la mesura, més petit serà
l'error relatiu de la mesura.
20
ml. (Se suposa que és el màxim
valor per a la xeringa).
-
A partir del volum i la densitat hauràs de
fixar un valor de massa orientativa.
18,5
g. Ha de ser una mica inferior al valor
numèric del volum per tal que la densitat sigui inferior a 1.
Activitat 3 : Busquem els límits.
Els càlculs aquí són
els mateixos que a l'activitat 2 i, a més a més, estan exposats
a l'apartat d'anàlisi i tractament de les dades
Activitat 4: Si t'ha sobrat temps, posa una
mica d'imaginació i intenta fer un esbós d'un dispositiu per mesurar
la pressió a l'interior d'una ampolla amb un líquid (manòmetre).
Es podria col·locar una proveta
invertida a l'interior de l'ampolla. A partir d'una gràfica o d'una
fórmula en un full de càlcul es podria calcular la pressió.

|

 6/8
6/8