núm 19 |
2017 |
Societat Catalana de Física |
| Inici |
| Sumari |   8/8 8/8 |
| El racó obscur: De la tossuderia d'Einstein a la rebel·lia de Bell Xavier Jaén |
|
| Fa aproximadament un any, el desembre de 2016, un munt de gent participa en un experiment anomenat The Big Bell Test, que havia de decidir sobre una qüestió també plantejada pel món de la filosofia: “Què és real?” o “Existeix la realitat per ella mateixa?”. En aquest racó mirarem d'explicar la base física que sustenta aquest experiment i la relació que té amb les qüestions filosòfiques subjacents. |
Introducció El 30 de novembre de 2016 més de 100.000 persones voluntàries
participaren en un experiment, que genera un flux de 1.000 bits per segon autènticament
aleatoris (cadenes de “0” i “1” a la babalà) que permetien garantir el
funcionament durant 48 hores d'un aparell que registrava el comportament d'unes
misterioses partícules entrellaçades. El resultat d'aquest experiment
havia de decidir sobre unes qüestions també plantejades pel món
de la filosofia, que tracta temes de tanta profunditat com “Què és
real?” o “Existeix la realitat per ella mateixa?”. És The Big Bell Test.
No és, ni de bon tros, la primera de les experiències d'aquesta
mena, però sí que és de sobres la que més participants
ha tingut. L'entusiasme dels participants, professorat i alumnat de molts centres
de secundària d'arreu del món, també de Catalunya, contrasta
amb la manca de coneixement del que es coïa. A les normals dificultats
per transmetre coneixement científic als no experts, s'hi afegeix el
caràcter fonamentalista d'aquest coneixement. Quàntica i filosofia.
Encara que una part dels receptors d'aquest coneixement, el professorat, són
persones capacitades per entendre la física subjacent, no sempre passa
que el problema que es planteja provoqui un terrabastall tan gran que arribi
a portar al laboratori qüestions que fins fa poc pertanyien al terreny
de la filosofia i, per tant, eren no decidibles en termes d'experimentació
objectiva. Les últimes vegades que algun experiment transcendent ha arribat
al gran públic, el missatge que s'ha transmès ha estat que s'havia
trobat alguna cosa. S'ha trobat una partícula fantàstica, el bosó
de Higgs. S'han trobat les ones gravitatòries. Evidentment que cal saber-ne
alguna cosa, sobre bosons de Higgs o sobre ones gravitatòries, per poder
entendre i valorar la gesta. Però com a mínim sabem que alguna
cosa nova tangible s'ha trobat. I això s'entén bastant bé.
En el cas del Big Bell Test, no s'ha trobat cap nou objecte o entitat física.
No s'ha respost a una qüestió més o menys comprensible del
tipus Existeix tal o qual cosa? El repte que tenim ara és fer entendre
quina és la qüestió a la qual s'ha donat resposta. Partícules amb spinLes partícules elementals tenen un moment angular intrínsec
o, com s'anomena en mecànica quàntica, spin. Exceptuant els efectes
quàntics, l'spin és l'anàleg a la rotació intrínseca
d'un cos. Per exemple, l'spin de la Terra seria la rotació diària
al voltant de l'eix que passa pel seu centre de masses. Quan construïm
els fonaments de la mecànica clàssica treballem amb partícules
conceptuals sense rotació intrínseca, sense spin, de moment angular
intrínsec nul. Les partícules conceptuals clàssiques són
tan petites “com vulguem”. Amb moltes partícules conceptuals en construïm
una de real, per exemple una baldufa. El moment angular de la baldufa s'explica
per la rotació orbital de les infinites partícules conceptuals
que la componen. Quan fem mecànica quàntica i estudiem el món
petit —limitadament petit!—, les partícules deixen de ser entitats conceptuals
per tenir existència i propietats intrínseques. Tenen massa, poden
tenir càrrega, com les partícules conceptuals de la mecànica
clàssica, però també rotació intrínseca,
tenen spin. L'electró és l'exemple més conegut. El valor
d'aquest spin no pot ser qualsevol, depèn de la partícula i del
seu entorn. Per exemple, en el cas dels electrons aïllats, poden tenir
spin en una direcció i sentit de l'espai qualsevol però amb un
valor determinat
Sabem mesurar l'spin utilitzant camps magnètics no uniformes
en experiències del tipus Stern-Gerlach. Tampoc ens cal entrar ara en
detalls tècnics. Representarem l'aparell de mesura com un filtre.
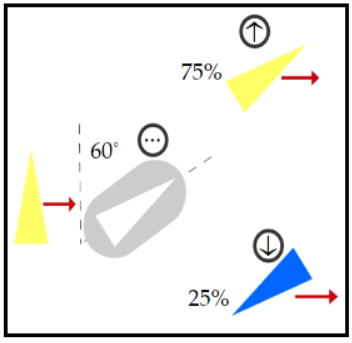
Vegeu la figura 1. Si volguèssim mesurar l'spin de tot un seguit d'electrons
amb la mateixa direcció i sentit d'spin, aniríem variant l'orientació
del filtre fins que detectéssim que el 100%
dels electrons tenen el mateix comportament. L'spin d'aquests electrons estarà
en la direcció del filtre amb un valor mesurat Més que aparell de mesura nosaltres en diem
filtre perquè no l'utilitzarem directament per fer mesures.
L'utilitzarem en diferents direccions de l'espai com a filtre per veure què
passa . Només en el cas que el filtre estigui en la direcció
de l'spin podem dir que estem mesurant en el sentit clàssic del terme.
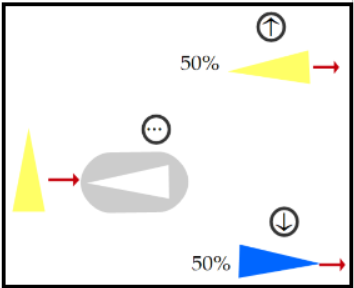
La probabilitat que l'electró sortint sigui groc o blau depèn de l'estat en què es trobi l'electró abans de passar el filtre. Aquestes probabilitats es poden calcular amb la mecànica quàntica i es poden corroborar amb l'experiència. Això no està sotmès a debat. Ens quedarem amb alguns d'aquest resultats:
Fins aquí hem treballat amb electrons, amb un spin definit, als quals hem fet passar per filtres en la direcció d'aquest spin o en altres direccions. Malgrat que hi ha efectes quàntics que poden sorprendre, encara res és rematadament estrany. Les partícules tenen un spin definit. Els fem passar per un filtre i aquest pot canviar l'spin, quan la direcció del filtre no coincideix amb l'spin original de la partícula, de manera no determinista, però sí que en sabem calcular ( amb la mecànica quàntica) i reproduir experimentalment (amb filtres del tipus Stern-Gerlach) la probabilitat que això passi.
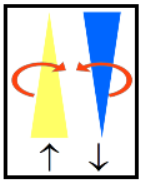
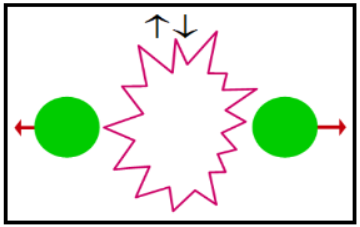
Conservació de l'spin total. Partícules entrellaçadesTreballarem amb partícules amb spin no definit. Encara més, treballarem amb partícules entrellaçades. Partim d'un sistema de dues partícules, dos electrons, amb espins oposats de manera que el sistema té un spin total zero. Tinguem en compte que en quàntica dues partícules pròximes no són distingibles. Parlar de dues partícules és només una manera d'esmentar-ne els ingredients. El que formen aquestes dues partícules és una entitat anomenada singlet. L'spin total, si no introduïm més spin, es conservarà. Sense alterar aquesta característica separem simètricament les partícules. El resultat és el de dues partícules allunyant-se amb espins oposats. No podem dir en quina direcció tenen l'spin, quina és groga i quina blava, mentre no la mesurem. Hem fabricat dues partícules entrellaçades. Podem dir que són esferes verdes (goc+blau) . Una esfera verda surt cap a la dreta, que en direm D i l'altra cap a l'esquerra, E. Vegeu la figura 7.
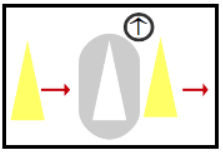
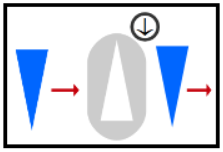
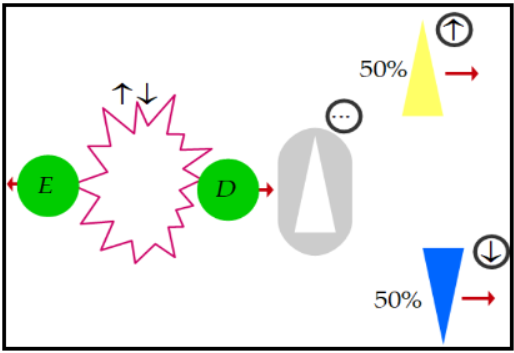
L'explicació estrictament quàntica d'aquest fet és la
següent: en el mateix instant en què D travessa
el filtre i passa de tenir un spin no definit a un de definit, per exemple groc,
d'alguna manera envia un senyal a la E perquè
passi de tenir un spin no definit a un de definit, en aquest cas blau, preservant
sempre la conservació de l'spin. Vegeu la figura 9.
Això és estrany, és molt estrany. Però és
només estrany per als no experts i només ens resta esperar uns
anys perquè ens hi acostumem? O és estrany de debò? La paradoxa EPREl 1935 Albert Einstein es va reunir amb els seus col·legues
Boris Podolsky i Natan Rosen per mirar de treure l'entrellat de la quàntica.
Aquest trio de físics es coneix amb les sigles EPR i proposaren la
paradoxa d'EPR. Principi de localitatLa relativitat d'Einstein prohibeix que els cossos materials viatgin a velocitats superiors a la de la llum. La llum, i, en general, les partícules de massa nul·la, són les úniques entitats que van a aquesta velocitat. Hom pot inferir d'aquí que no és possible l'intercanvi d'informació a una velocitat més gran que la de la llum. D'aquí prové el principi de localitat, que van enunciar amb aquests termes:
|
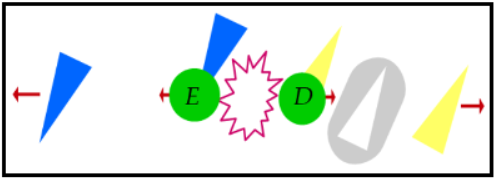 |
| Fig. 10 |
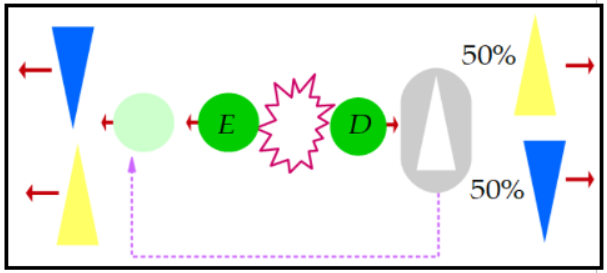
EPR proposaven que les partícules verdes D i E, sense spin definit en aquell moment, tenien variables ocultes que determinaven quin spin tindrien, groc o blau, si passaven per filtres per a totes les direccions de l'espai. Només calia que, per a cada direcció, el valor de la variable oculta de E tingués el sentit d'spin contrari a D. A les figures podem veure possibles valors de les variables ocultes per a tres direccions de l'espai. Vegeu la figura 11.
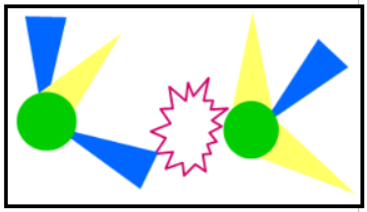 |
| Fig. 11 |
La proposta EPR, tot i ser tècnicament agosarada, estava
completament d'acord amb els principis de localisme i realisme.
No era, però, una proposta que poguéssim testar experimentalment.
Les dues propostes donen valors estadístics iguals (groc
o blau) per a direccions fixes de l'espai. Donada una direcció
de l'espai, el 50%
de partícules D donaven groc ( i, posteriorment
les E blau) i el 50%
de partícules D donaven blau (i, posteriorment
les E groc) tant fos en la hipòtesi de les
variables ocultes, sense variables ocultes i, per descomptat, experimentalment.
L'únic argument per preferir les variables ocultes, acceptant,
per tant, dir que la mecànica quàntica no era una
teoria completa i que les probabilitats quàntiques eren només
fruit de la nostra ignorància, eren els principis de realisme
i localisme. Aquest principis eren, són, molt raonables,
sí, però de cap manera provats.
Si es compleixen els principis de localisme i realisme la mecànica quàntica no és una teoria completa i les probabilitats quàntiques són un reflex de la nostra ignorància.
Com que s'acceptaven aquests dos principis, la conclusió d'EPR és
la que hem ressaltat en negreta. Aquesta conclusió és la que,
amb no gaire entusiasme, va dominar la interpretació de la mecànica
quàntica d'ençà que EPR publiquen l'article. Tinguem en
compte que el seu argument es basa en dos principis. No varen fer cap proposta
que es pogués testar experimentalment. Einstein Podolsky i Rosen conclouen
que la mecànica quàntica no es completa basant-se en supòsits
molt bàsics però no contrastats. Per a la majoria de físics
si no hi ha una manera de decidir-nos entre dues opcions per mitjà de
l'experimentació, es tracta de pura filosofia. I la filosofia és
per als filòsofs. I així va quedar la cosa.
El test de Bell
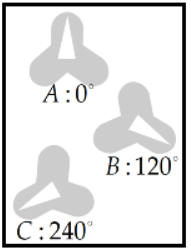 |
| Fig. 12 |
Pels volts de 1964 l'irlandès John S. Bell treballava
al CERN dedicat al disseny d'acceleradors per a l'experimentació amb
partícules elementals. Però tenia un hobby ocult. Possiblement
molts físics quàntics tenien el mateix hobby després
del 1935. Donava voltes i més voltes a la paradoxa d'EPR per mirar de
trobar quelcom de mesurable que pogués decidir si la quàntica
era una teoria completa o no, sense apel·lar a cap altre principi ...
I ho trobà! És el test de Bell.
Després del descobriment de Bell altres autors han anat trobant formes més o menys semblants del test de Bell amb algunes millores conceptuals i tècniques que els fan més aptes per a dur-los a la pràctica. Destacarem la forma donada por John Clauser, Michael Horne, Abner Shimony i R. A. Holt, coneguda com la forma CHSH, ja que és la que s'ha fet servir en el Big Bell Test. Com que ni volem ni podem afinar tant, en aquest racó explicarem la forma original del test de Bell.
Bell proposa fer passar per filtres independents cadascuna de les dues partícules
entrellaçades. Aquest filtres podrien estar en tres direccions.
La direcció ![]() ,
la
,
la ![]() i
la
i
la ![]() .
Vegeu la figura 12.
.
Vegeu la figura 12.
Així per exemple, es pot fer passar les partícules entrellaçades
D i E per filtres segons els angles A
i C, tal com es veu a la figura 13.
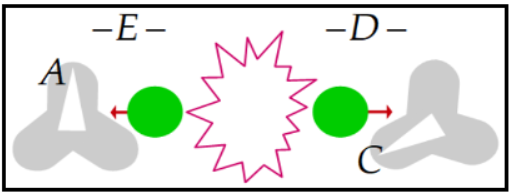 |
| Fig. 13 |
Per fer l'experiència transparent les direccions dels filtres A,
B o C canvien aleatòriament a un ritme
prou ràpid perquè no sigui possible enviar la informació
d'aquest canvi d'un filtre a l'altre. Destaquem aquest punt perquè és
aquí on, anys més tard, rau el protagonisme dels voluntaris participants
en el Big Bell Test: proporcionar la cadena aleatòria que comanda els
canvis de direcció dels filtres a un ritme de temps més ràpid
que el que trigaria la llum a anar d'un filtre a l'altre. Però seguim
el fil argumental de la proposta de Bell.
Tenim un parell de filtres que canvien de direcció aleatòriament i independentment l'un de l'altre d'entre tres possibilitats. Vegeu la figura 14..
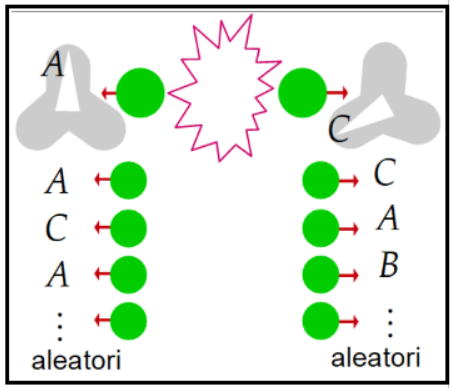 |
| Fig. 14 |
Es van enviant parelles de partícules entrellaçades i els filtres van produint resultats grocs o blaus en les direccions A, B o C aleatòriament canviants. El que finalment es registra és el nombre de vegades que el resultat del pas pels filtres D i E són:
coincidents:(groc-groc) o
(blau-blau): resultat
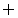
oposats:
(groc-blau) o
(blau-groc): resultat
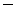
Recordem que un spin és ![]() (groc)
quan en passar pel filtre surt coincidint amb la direcció i sentit del
filtre. Així
(groc)
quan en passar pel filtre surt coincidint amb la direcció i sentit del
filtre. Així ![]() (groc-blau)
en el cas de les direccions A i C vol dir
que el filtre E dona un spin
(groc-blau)
en el cas de les direccions A i C vol dir
que el filtre E dona un spin ![]() (groc)
en la direcció i sentit
(groc)
en la direcció i sentit ![]() i
D dona un spin
i
D dona un spin ![]() (blau)
en la direcció i sentit
(blau)
en la direcció i sentit ![]() .
.
Quan Bell proposa tot aquest enrenou no hi havia els mitjans tècnics
per fer realment l'experiència. Va provocar més rebombori entre
pensadors i filòsofs que entre físics. Es veia com a molt sorprenent
que la física pogués decidir en aquest tipus de debats filosòfics.
Però com que tècnicament això no era possible... doncs
van anar allargant el debat.
Finalment, aquesta experiència es va poder fer. En la manera en què
Bell ho pensà, el primer que va fer l'experiència va ser l'equip
d'Alain Aspect el 1982, la qual s'ha repetit molts cops amb moltes variants
tècniques per millorar-ne la fiabilitat. Un dels aspectes en què
el test ha anat millorant és la distància entre els filtres detectors.
Poca broma, estem parlant de distàncies per sobre del centenar de kilòmetres!
El Big Bell Test de finals del 2016 és un d'aquest experiments.
Ara podem donar el resultat d'aquestes experiències, però si no tenim una predicció del que diu la teoria no sabrem interpretar-ho. El gran mèrit de John S.Bell és que va deduir la predicció d'aquest experiment factible des del punt de vista de les variables ocultes (que no és quàntica) i des del punt de vista de la mecànica quàntica i que aquestes prediccions són diferents!
Predicció segons les variables ocultes
Introduïm variables ocultes per a les tres direccions de l'espai, A,
B i C. Això és, cada partícula
verda portarà també la informació sobre com s'ha de comportar
en el cas d'haver de passar per un dels tres filtres. Aquesta comportament ha
d'estar d'acord amb la conservació de l'spin. Tenim bàsicament
dues opcions. Vegeu la figura 15.
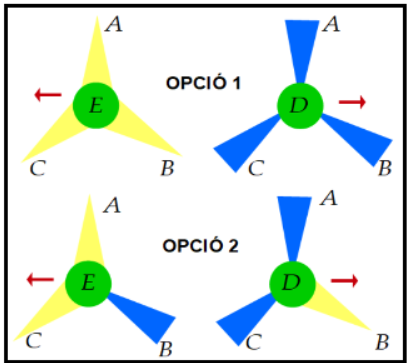 |
| Fig. 15 |
L'opció 1 en la qual la partícula E és tot groc, amb la D corresponent, és a dir tot blau.L'opció 2 en la qual la partícula E té una direcció blava i les altres grogues, amb la D corresponent.
Les altres possibles opcions són rotacions de ![]() i/o
intercanvis de D i E, i, per tant, donaran
resultats semblants per al que ens interessa.
i/o
intercanvis de D i E, i, per tant, donaran
resultats semblants per al que ens interessa.
Què vol dir, per exemple, què la parella de partícules
entrellaçades tingui les variables ocultes segons l'opció 2?.
Doncs que si E passa per un filtre B donarà
blau i si D passa per un filtre C donarà
també blau però en canvi, si D passa per un filtre
B donarà groc.
Les posicions dels filtres, quan passen les partícules entrellaçades,
poden ser aleatòries entre les 9
possibilitats dels filtres AA, BB, CC,
AB, BA, AC, CA,
BC i CB. Volem comptabilitzar els resultats
coincidents:(groc-groc) o
(blau-blau): resultat
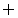
oposats:
(groc-blau) o
(blau-groc): resultat
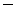
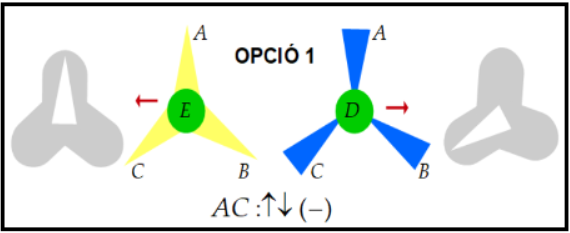 |
| Fig. 16 |
Observant detingudament les figures 16 i 17 corresponents a les opcions 1 i
2, si anem canviant les posicions dels filtres en les tres direccions, és
senzill de veure que l'opció 1 sempre dona resultat
![]() . L'opció 2
dona resultat
. L'opció 2
dona resultat ![]() en les 5 posicions dels filtres AA, AC,
CA,CC i BB. Una proporció
5/9. En les posicions
AB, BA, B i CB
dona un resultat
en les 5 posicions dels filtres AA, AC,
CA,CC i BB. Una proporció
5/9. En les posicions
AB, BA, B i CB
dona un resultat ![]() .
.
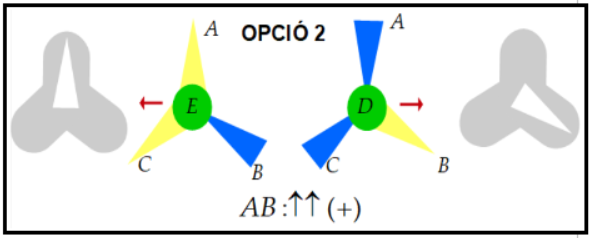 |
| Fig. 17 |
Si només tinguéssim partícules entrellaçades
amb l'opció 2 ( o rotacions de ![]() i/o
intercanvis de D i E) 5 de cada
9 resultats, és a dir, un 5/9
= 55,5%, tindrien un resultat
i/o
intercanvis de D i E) 5 de cada
9 resultats, és a dir, un 5/9
= 55,5%, tindrien un resultat ![]() .
Com que també hi ha la possibilitat que les partícules
entrellaçades surtin amb variables ocultes segons l'opció
1, que sempre dona resultat
.
Com que també hi ha la possibilitat que les partícules
entrellaçades surtin amb variables ocultes segons l'opció
1, que sempre dona resultat ![]() per
a totes les posicions dels filtres, el resultat final haurà
de ser que:
per
a totes les posicions dels filtres, el resultat final haurà
de ser que:
UN ![]() DONARÀ
RESULTAT
DONARÀ
RESULTAT ![]()
Fixem-nos que, sense entrar a veure quina és la predicció de
la mecànica quàntica, ja podríem fer l'experiment i, si
el resultat és un ![]() ,
podríem descartar les variables ocultes com a explicació bona.
Per completar-ho vegem quina és la predicció de la mecànica
quàntica.
,
podríem descartar les variables ocultes com a explicació bona.
Per completar-ho vegem quina és la predicció de la mecànica
quàntica.
Predicció segons la mecànica quàntica
Tindrem en compte els resultats quàntics donats més amunt, en
particular Rd: si fem passar una partícula amb un spin
definit en una direcció ![]() per
un filtre inclinat 60º
respecte de la direcció
per
un filtre inclinat 60º
respecte de la direcció![]() ,
hi ha un 75% = 3/4
de probabilitats que segueixi
,
hi ha un 75% = 3/4
de probabilitats que segueixi ![]() i un 25% =1/4 que
canviï a
i un 25% =1/4 que
canviï a ![]() .
.
Ara no hi ha variables ocultes. Només partícules entrellaçades
verdes i les 9 possibles posicions dels filtres AA, BB,
CC, AB, BA, AC,
CA, BC i CB.
Si el primer filtre que actua, diguem el filtre E, detecta
un spin ![]() , llavors
sabem que la partícula D té l'spin en la mateixa
direcció però
, llavors
sabem que la partícula D té l'spin en la mateixa
direcció però ![]() .
I això abans que passi pel filtre!
.
I això abans que passi pel filtre!
Les situacions que ens podem trobar són essencialment les que hi ha a
les dues figures 18 i 19 (rotacions de ![]() i/o
intercanvis de D i E, i canvis entre groc
i blau són semblants): filtres paral·lels o filtres
i/o
intercanvis de D i E, i canvis entre groc
i blau són semblants): filtres paral·lels o filtres ![]() .
.
 |
| Fig. 18 |
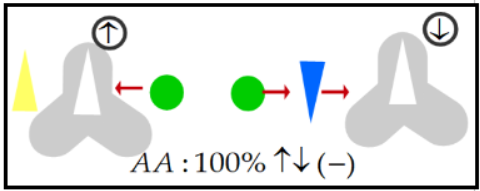
Filtres paral·lels: passarà 1/3
dels cops (a causa de la aleatorietat de les posicions dels filtres),
donen sempre (100%=1)
resultat ![]() .
.
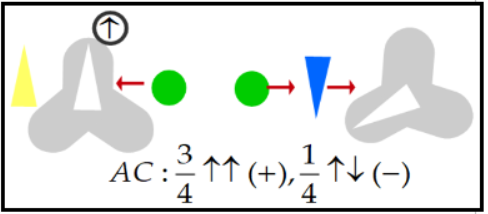
Filtres ![]() :
passaran 2/3
dels cops (a causa de la aleatorietat de les posicions dels filtres) donen 1/4
un resultat
:
passaran 2/3
dels cops (a causa de la aleatorietat de les posicions dels filtres) donen 1/4
un resultat ![]() i
3/4 un resultat
i
3/4 un resultat
![]() .
.
 |
| Fig. 19 |
Així, el percentatge total de vegades que tenim resultat
![]() és:
és:
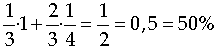
La conclusió és que segons la mecànica quàntica:
UN ![]() DONARÀ
RESULTAT
DONARÀ
RESULTAT ![]()
Resultat de l'experiència
S'han fet, com hem comentat, múltiples experiències. No podem
donar els resultats de les diferents experiències perquè cadascuna
parteix d'un disseny diferent i respon a una predicció diferent tant
des del punt de vista de les variables ocultes com des del punt de vista de
la mecànica quàntica. En resum podem dir que els diferents experiments
que s'han dut a terme, traduïts al disseny original de Bell que hem presentat,
és
UN ![]() DONA
RESULTAT
DONA
RESULTAT ![]()
La conclusió experimental és que la mecànica quàntica és una teoria completa, que de variables ocultes res de res i que els principis de realisme i localisme o són simples prejudicis ( que funcionen la mar de bé en la vida quotidiana però no són principis absoluts) o estan mal plantejats o totes dues coses alhora.
Conclusions
Hem mirat d'entendre l'entrellat de la mecànica quàntica. Hem pogut definir bé quina era la qüestió. Hem pogut dissenyar un test per veure qui té raó. Ara ja sabem qui té raó:
La mecànica quàntica és una teoria completa, és a dir, les probabilitats quàntiques són intrínseques del comportament de les entitats físiques. La realitat no és un concepte objectiu i les entitats físiques es poden influenciar instantàniament a distància.
Aquest és el resultat més o menys traduït
en paraules. Ens en podem anar a dormir tranquils? No! La conseqüència
immediata és que la mecànica quàntica augmenta la seva
aurèola de teoria misteriosa i incompresa. Tenim tots plegats molta més
feina que el mateix Einstein per esbrinar per què la natura és
com és...si és que, després de l'ensopegada del
realisme, podem parlar així! Potser el que hem de fer és canviar
els nostres punts de vista a veure si les coses s'entenen millor. Potser és
que atorgar a la natura una realitat i una explicació és una tasca
molt més “humana” del que ens pensàvem? Potser...
Algunes fonts d'informació
- The original EPR paper. http://prola.aps.org/abstract/PR/v47/i10/p777_1
- The Big Bell Test: https://thebigbelltest.org/ca/resultats
- J. S. Bell, On the Einstein Podolsky Rosen Paradox, Physics 1, 195 (1964)
http://www.drchinese.com/David/Bell_Compact.pdf
- J. F. Clauser, M. A. Horne, A. Shimony and R. A. Holt, Proposed experiment
to test local hidden-variable theories, Physical Review Letters 23, 880–884
(1969)
- Bell's Theorem with Easy Math: http://drchinese.com/David/Bell_Theorem_Easy_Math.htm
- Quantum Entanglement & Spooky Action at a Distance https://www.youtube.com/watch?v=ZuvK-od647c




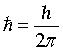 on
on