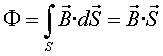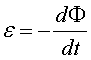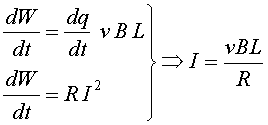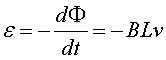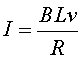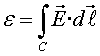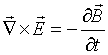
La llei de Faraday

Introducció

En aquest número tractem un embolic força habitual que molt poques vegades hom veu desenredar de manera clara. Els embolics no es fan de manera espontània. De fet molts cops, a causa de a la seva història, és lògic que existeixin i persisteixin, almenys per a certs col·lectius que hi poden conviure sense cap problema. La llei de Faraday és un d'aquests casos paradigmàtics. És una llei molt "popular". Diferents professionals la fan servir en multitud de situacions. Però què diu exactament la llei de Faraday? Deixem aquesta qüestió per a més endavant i comencem per repassar les coses que sabem.

La llei de Faraday

Michael Faraday va descobrir la inducció i va proposar la llei que porta el seu nom sobre una base absolutament experimental pels volts del 1831. Aquí tractem amb la formulació actual de la llei de Faraday.
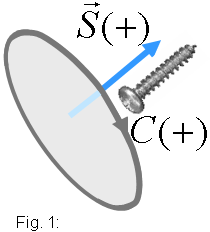
Si tenim una superfície S, com la de la figura 1, la podem tenir orientada a l'espai de moltes maneres. Aquest fet es pot expressar amb un vector 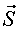. Un cop orientada la superfície tindrem clar quin és el sentit positiu en travessar la superfície i també, amb la regla del cargol (dextrogir), quin és el sentit positiu de recorregut del seu contorn. Així si calculem el flux magnètic per a un camp uniforme

(1)

serà el signe de 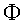el que ens dirà si aquest travessa en un sentit o en l'altre a la superfície. La llei de Faraday, tal com habitualment s'expressa, diu que si el flux que travessa la superfície d'un circuit de material conductor tancat varia llavors s'aprecia en el circuit una força electromotriu donada per: (2)    Si, com hem esmentat anteriorment hem tingut cura de definir l'orientació de la superfície, com a la figura 1, per exemple, llavors una ens indica que el corrent induit té el sentit de recorregut positiu (com el C(+) de la figura) i una indica un senit del corrent contrari al C(+).

La llei de Lorentz

Hendrik Lorentz va ser el responsable d'expressar els efectes del camp magnètic sobre una partícula en moviment com una força, pels volts del 1892. Aquests efectes van ser anteriorment estudiats i reconeguts com a efectes magnètics per James Clerk Maxwell cap al 1861(On Physical Lines of Force, pàg. 342). La llei de Lorentz (o força de Lorentz) és la llei que dóna significat físic al camp magnètic. Si una càrrega q es passeja per l'espai amb velocitat en presència d'un camp magnètic , rep la força següent: (3)    Per veure quina direcció i sentit té aquesta força podem fer servir la regla del cargol dextrogir, tal com es veu a la figura. És preferible utilitzar la regla del cargol en lloc de la regla de la mà dreta, primer per respecte als esquerrans i segon perquè no tothom és capaç d'imaginarse una mà dreta independent del cos i situada allà on la necessitem. En canvi, sempre podem portar un cargol a sobre i situar-lo allà on el necessitem i fer-lo girar per veure cap a on avança. Amb una mica de pràctica ja no ens caldrà portar a sobre el cargol!

Problemes d'inducció amb la llei de Lorentz

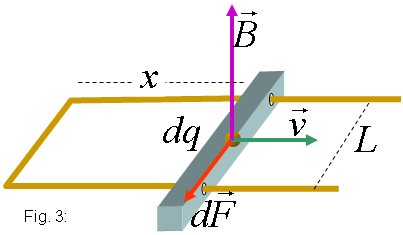
Forcem una barra de resistència R i longitud L a moure's amb velocitat constant cap a la dreta sense perdre el contacte amb unes guies conductores ideals tancades per l'esquerra (vegeu la figura 3). El pla format per les guies i la barra és travessat per un camp magnètic uniforme.

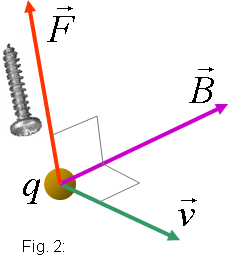
Totes les càrregues de la barra, i en especial les de la banda de conducció, viatgen a velocitat v com la barra. Sigui dq un trosset de càrregues. A causa de la presència del camp magnètic i de la llei de Lorentz aquest trosset rep la força següent:

(4)

Així, aquest trosset està sotmès a una força durant un trajecte L . El treball realitzat per la força és:

(5)

Com que hi ha una resistència, passada la fase transitòria, en què les càrregues inicien el seu moviment al llarg de la barra, aquest treball es dissipa per efecte Joule. Així, si I és la intensitat estacionària, prenent el dt que triga a passar el trosset dq, tenim dq=Idt i podem escriure: (6)    Aquesta és una intensitat induïda. Notem que no ens ha fet cap falta parlar de camps elèctrics ni de diferències de potencial!

Problemes d'inducció amb la llei de Faraday

Forcem una barra de resistència R i longitud L a moure's amb velocitat constant cap a la dreta sense perdre el contacte amb unes guies conductores ideals tancades per l'esquerra (vegeu la figura 4). El pla format per les guies i la barra és travessat per un camp magnètic uniforme.

La barra i els tres costats de les guies conductores formen un circuit tanca per on pot circular un corrent. Podem aplicar la llei de Faraday

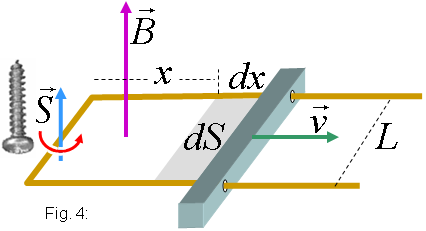
Escollim el vector superfície orientat tal com es veu a la figura 4. El recorregut positiu del circuit és així l'indicat per la fletxa corbada de color vermell de la figura. En un instant donat, en què la barra està situada a x de l'extrem esquerra, el flux de camp magnètic val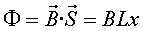. Aplicant la llei de Faraday tenim

(7)    i en conseqüència el corrent induïtt és negatiu (de signe contrari a l'indicat en vermell a la figura 4), i en valor absolut I val (8)    El resultat (valor absolut i sentit ) coincideix amb el que s'ha obtingut amb la llei de Lorentz (34).

Què diu exactament la llei de Faraday

Ara podem respondre amb propietat a aquesta qüestió. La llei de Faraday inclou dos fenòmens.

• Si els circuits conductors es mouen en el si d'un camp magnètic estàtic s'aprecien corrents induïts gràcies a la llei de Lorentz, no a la de Faraday. La llei de Faraday no diu res de nou en aquest aspecte. El que proporciona és un mètode de càlcul relativament senzill per trobar els corrents induïts. La llei de Faraday és únicament una alternativa de càlcul dels efectes sobre el circuit de la força de Lorentz. No apareix cap camp elèctric ni és necessari. Les càrregues es mouen al llarg del circuit perquè porten una velocitat tranversal en el si d'un camp magnètic.
  
• Si els circuits conductors son travessats per un camp magnètic variable en el temps, llavors s'aprecien corrents induïts gràcies a la llei de Faraday. Ara la llei de Lorentz no diu ni preveu res en aquest aspecte. Atès que la velocitat de les càrregues tranversal al circuit és nul·la, la força de Lorentz alineada amb el circuit també és nul·la! Notem ara que no podem atribuir un origen magnètic a la força responsable del moviment, i que per tant hem d'aadmetre que apareix un camp elèctric, de manera que al llarg del circuit:

  (9)

  És per això que, quan s'escriuen les equacions de Maxwell, la llei de Faraday (2) es reescriu de manera que no interfereixi amb altres lleis, com (3), en termes de sistemes de referència inercials en la forma més coneguda com a tercera llei de Maxwell:
  

  (10)

  A aquesta equació s'hi arriba utilitzant (2) juntament amb (9), aplicada a qualsevol camí tancat, sigui un circuit de material conductor o un traçat imaginat a l'espai, i amb el teorema de Stokes. Einstein i la relativitat acabaran d'arreglar el que s'ha d'entendre exactament per "sistema de referència inercial", però això és tota una altra història.

Sumari

7/8

Inici	Com podeu col·laborar?	Subscripció
ISSN: 1988-7930    Adreça a la xarxa: www.RRFisica.cat    Adreça electrònica: redaccio@rrfisica.cat  difusio@rrfisica.cat Comitè de redacció : Josep Ametlla, Octavi Casellas, Xavier Jaén, Gemma Montanyà, Cristina Periago, Octavi Plana, Jaume Pont i Ramon Sala. Treballem conjuntament : Societat Catalana de Física, Associació de Professores i Professors de Física i Química de Catalunya,XTEC, Universitat Politècnica de Catalunya, Universitat de Barcelona
Programació web: Xavier Jaén i Daniel Zaragoza. Correcció lingüística: Serveis Linguïstics de la Universitat Politècnica de Catalunya.		Aquesta obra està subjecta a una Llicència de Creative Commons
Recursos de Física col·labora amb la baldufa i també amb ciències Revista del Professorat de Ciències de Primària i Secundària (Edita: CRECIM-UAB)