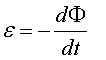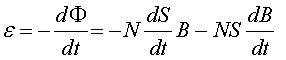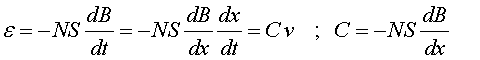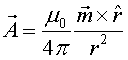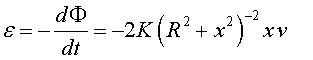núm 5 |
Primavera del 2010 |
Societat Catalana de Física |
| Inici |
| Sumari |   3/9 3/9  |
| Caiguda lliure d'un imant Basili Martínez i Xavier Jaén |
|
| Presentem una activitat, la caiguda lliure d'un imant travessant una bobina, que lliga la mecànica (caiguda lliure) amb l'electromagnetisme (llei de Faraday). Aquesta activitat es pot fer servir a diferents nivells segons si ens quedem amb la descripció del fenomen o anem més enllà fins a caracteritzar l'imant calculant-ne el moment magnètic. |
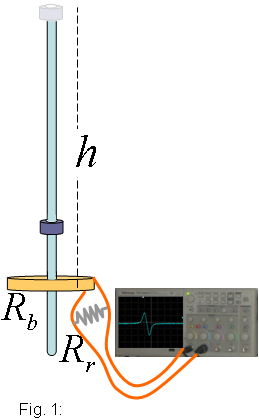
IntroduccióEn aquest article descriurem una activitat que ens pot ajudar a comprendre el fenomen de la inducció electromagnètica, utilitzant materials d’ús habitual al laboratori. Es pot fer servir en cursos de segon cicle d’ESO de forma qualitativa, i al batxillerat fent els càlculs que es proposen. Fonamentalment, es tracta de fer lliscar un imant en forma d’anell per una vareta de vidre que està en posició vertical i que en al seu punt mig conté una bobina. Depenent de l’altura de sortida de l’imant tindrem diferents velocitats i diferents voltatges induïts. També podem experimentar altres variacions, com fer lliscar dos imants iguals units o fer la prova amb un potent imant de neodimi, o també podem canviar la polaritat dels imants, canviant-ne l'orientació, i observar si es produeixen canvis en el voltatge induït. L’article conté també una part més teòrica, dirigida al professorat, que intenta explicar la complexitat del fenomen. Guia del professoratEl fenomen
Així,
L'experiència la fem amb una bobina amb un nombre d'espires
que no és gaire elevat i afegint-hi una resistència Rr
relativament gran, de manera que puguem negligir els efectes d'autoinducció
i les pèrdues per l'efecte Joule de la bobina. En aquestes condicions
i segons el model teòric,
on N és el nombre d'espires, R és el radi i m el moment magnètic de l'imant, la quantitat que el caracteritza com a tal. H està relacionada amb el gruix de la bobina. Per simplificar hem considerat dos possibles models de bobina:
Mesures de El materialA ccontinuació us donem les dades del material utilitzat. L'experiència també funcionarà utilitzant imants, bobines i resistències semblants a les que descrivim aquí. L'element més delicat potser és l'oscil·loscopi.
Noteu que la resistència i la bobina compleixen la relació (24), que governa la importància relativa dels efectes magnètics secundaris (vegeu la secció Un model teòric més avall en aquest mateix article):
Activitats al voltant de l'experiènciaAquesta activitat ésta pensada per fer-la al laboratori. Així, l'alumnat trobarà el material preparat per fer el muntage o el muntatge ja fet. El professorat podrà adaptar les activitats al nivell de l'alumnat segons els punts seqüents: 1) Ens podem quedar amb la part fenomenològica, observant el fenomen i discutint les gràfiques de l'oscil·loscopi però sense arribar a prendre dades. En aquest nivell es pot parlar qualitativament de les energies cinètica, gravitatòria i magnètica (i també de pèrdues de calor per l'efecte Joule i pel fregament) i com d'unes es passa a les altres. 2)Acceptant que l'energia bescanviada a la bobina
és molt petita comparada amb la gravitatòria total, podem prendre
dades i observar la linealitat 3)Podem fer el càlcul del pendent P
de la recta 4) Amb el valor de m , per a alguna h , podem calcular l'energia magnètica de la bobina i corroborar que és molt més petita que la gravitatòria.
on 5) Per acabar, podem fer servir l'expressió
del moment magnètic d'una bobina, A la Guia de l'alumnat que proposem ens quedarem al punt 2, ja que la resta de punts poden quedar fora de l'àmbit del batxillertat i a més són només de càlcul. A continuació donem els resultats que s'obtenen amb el material utilitzat. Dades i resultats
Guia de l'alumnatIntroduccióEn aquesta pràctica fareu un experiment que us pot ajudar a comprendre el fenomen de la inducció electromagnètica, utilitzant materials d'ús habitual al laboratori. Fonamentalment, es tracta de fer lliscar un imant en forma d'anell per una vareta de vidre que està en posició vertical i que al seu punt mig conté una bobina. Depenent de l'altura de sortida de l'imant tindrem diferents velocitats i diferents voltatges induïts. Fonament teòricFareu una experiència relacionada amb la llei de Faraday-Lenz.
Aquesta llei ens diu que el voltatge induït És a dir, la variació del flux magnètic
El primer terme és igual a zero, ja que la superfície és la d'una bobina en repòs i per tant és constant. Si tenim en compte que l'imant es mou amb una trajectòria rectilínia x(t) tindrem B(x(t)) , i aplicant la regla de la cadena
És a dir, el voltatge induït és, amb la posició
fixada , proporcional a la velocitat. Si x
és la posició de l'imant respecte de la bobina, hi haurà
una posició per a la qual el voltatge induït arriba al seu valor
màxim,
Procediment experimental Fixeu el tub de vidre amb un suport i amb l'ajuda de dues pinces de manera
que quedi en posició perfectament vertical, marqueu amb un retolador
altures de 10 cm
a partir del nivell de la bobina. La bobina feu-la aguantar amb un altre suport
i una pinça, independents dels primers, i al final del tub de vidre poseu-hi
un tros de cordó de tela que esmorteirà el cop i evitarà
que es trenqui l'imant.
Deixeu anar l'imant de les diferents altures que heu marcat i llegiu el voltatge
màxim Vrmax
, i amb (8) trobeu
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| h
(m) |
|
Vrmax
(V) |
|
|
0,1
|
||||
0,2 |
||||
0,3 |
||||
0,4
|
||||
0,5 |
||||
| 0,6 |
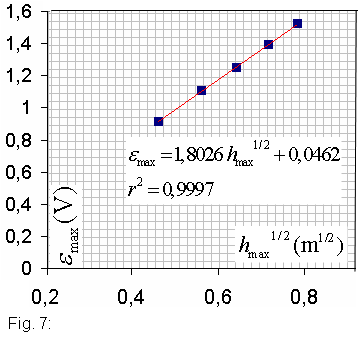
Representació gràfica
Amb aquestes dades feu la representació gràfica ![]() i
i ![]() .
.
Conclusions i qüestions
A partir de les dades i dels gràfics obtinguts responeu a les qüestions següents:
1) Quina relació de dependència
es pot deduir de la gràfica entre velocitat,![]() ,
i
,
i ![]() .
Es compleixen les previsions fetes a l'apartat de fonaments teòrics?
.
Es compleixen les previsions fetes a l'apartat de fonaments teòrics?
2) Quina relació de dependència
es pot deduir de la gràfica entre ![]() i
i
![]() ? Es
compleixen les previsons fetes a l'apartat Fonament teòric?
? Es
compleixen les previsons fetes a l'apartat Fonament teòric?
3) Si posem dos imants junts, què
creus que passarà si doblem el camp magnètic de l'imant?.
4) Què creus que passarà
si girem l'imant, canviant la polaritat nord-sud?.
5) Què creus que passaria si augmentéssim la massa de l'imant amb un material diamagnètic?
6) A partir dels resultats, calcula quina
velocitat hauria d'assolir l'imant en passar per la bobina per produir un voltatge
de 106 V.
7) A partir dels resultats, calcula quantes
voltes hauria de tenir la bobina per produir un voltatge màxim de 106
V.
8) Què et sembla que representarien
les gràfiques que ens dóna l'oscil·loscopi voltatge/temps
si calculéssim l'àrea o les integréssim?.
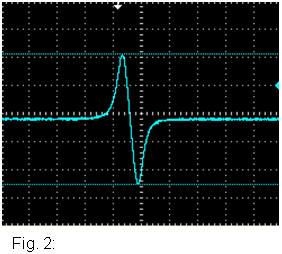
9) Explica com interpretes els canvis
de pendent que podem observar en les imatges obtingudes amb l'oscil·loscopi.
10) Quan a la bobina s'hi indueix el corrent, augmenta l'energia. D'on creus que prové aquesta energia?
11) A què creus que és
degut que la velocitat de l'imant no sigui, en realitat, exactament igual a
la que correspon segons la caiguda lliure?
12) El sentit del corrent induït té res a veure amb la conservació de l'energia?
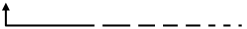
Un model teòric
A continuació construïm un model teòric del fenomen que tractem. Evidentment, el nivell supera el de secundària i no es tracta ni de bon tros que l'alumnat (de secundària) llegeixi aquest apartat. Pot servir al professorat per conèixer amb més profunditat el fenomen i també per una possible adaptació de l'activitat a nivell universitari.
El model
| Un magnet de petites dimensions i de moment
magnètic El magnet crea un camp magnètic que, per a punts relativament llunyans (respecte de les seves dimensions), sabem que té un potencial vector
El camp
|
 |
||||
|
|
Si la bobina és prima (les espires estan totes al mateix lloc), el flux que aquest camp hi provoca és
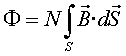 |
(11) |
on N
és el nombre d'espires de la bobina i ![]() la superfície encerclada per una espira.
la superfície encerclada per una espira.
Utilitzant el teorema de Stokes tenim
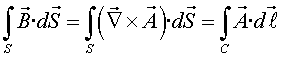 |
(12) |
on C és el contorn de la bobina. Noteu que d'aquesta manera podem calcular el flux utilitzant (12), ja que els punts del contorn C estaran sempre lluny del magnet.
Substituint (9) a (12) obtenim
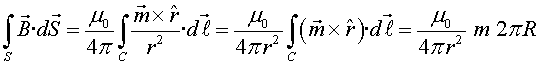 |
on hem utilitzat que r
és constant al llarg de C
i que ![]() és paral·lel
a
és paral·lel
a ![]() . Podem posar r
en funció de x
per obtenir
. Podem posar r
en funció de x
per obtenir
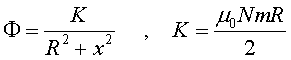 |
(13) |
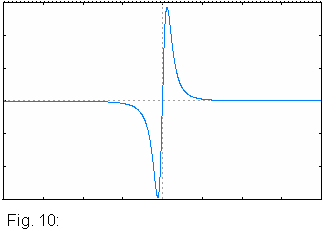
La força electromotriu induïda a la bobina és, segons la llei de Faraday:
A la figura podem veure de forma qualitativa el perfil de |
 |
El valor màxim d'aquesta vindrà donat per
(14) |
on ![]() són, respectivament,
la posició i la velocitat del magnet quan es dóna la variació
màxima de flux. Notem que si
són, respectivament,
la posició i la velocitat del magnet quan es dóna la variació
màxima de flux. Notem que si ![]() és independent de la velocitat del magnet (o altura des de la
qual el tirem) i només depèn de la geometria (de R),
llavors podem dir que la FEM màxima és proporcional a la velocitat.
També hem de fer notar que aquesta velocitat no és la que correspon
a una altura h
respecte de la posició de la bobina (és a dir x
= 0 ) sinó a una altura
és independent de la velocitat del magnet (o altura des de la
qual el tirem) i només depèn de la geometria (de R),
llavors podem dir que la FEM màxima és proporcional a la velocitat.
També hem de fer notar que aquesta velocitat no és la que correspon
a una altura h
respecte de la posició de la bobina (és a dir x
= 0 ) sinó a una altura![]() .
.
Així doncs, continuem per mirar d'esbrinar aquestes qüestions. Tornem a derivar el flux i igualem a zero
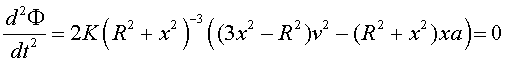 |
(15) |
Fixem-nos que si el magnet es mou amb una velocitat constant (a
= 0 ) llavors el màxim està situat a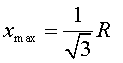 i és independent de la velocitat (o altura h).
Però el magnet cau, segons
i és independent de la velocitat (o altura h).
Però el magnet cau, segons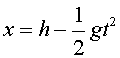 ,
és a dir,
,
és a dir, ![]() i
i![]() .
Fent la ssubstitució a (15) , tenim
.
Fent la ssubstitució a (15) , tenim
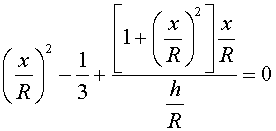 |
(16) |
Així, si h
és molt més gran que R
podem seguir mantenint que 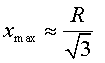 i
que
i
que ![]() . A més,
en aquest cas tindrem
. A més,
en aquest cas tindrem ![]() (
( ![]() ), i així
), i així
(17) |
Efectes secundaris
Tenim tres possibles efectes no contemplats d'entrada: a) efectes de fregament sec i aerodinàmic i b) efectes electromagnètics de segon ordre i c) el gruix de la bobina
a) Els possibles efectes de fregament aerodinàmic es
veuran afavorits per una h
gran i tendin a fer que la velocitat de caiguda arribi a la velocitat límit
i sigui constant. Encara es compliria ![]() i
i 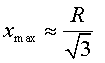 . Caldria però
esbrinar aquesta velocitat. No tindrem en compte aquests efectes.
. Caldria però
esbrinar aquesta velocitat. No tindrem en compte aquests efectes.
b) El magnet indueix corrents a l'espira i aquesta genera
un camp magnètic de sentit oposat. La situació és l'encarament
entre dos pols magnètics del mateix signe. Així doncs, la interacció
entre magnet i espira és de repulsió. A distàncies relativament
grans, mentre el magnet està caient, aquesta repulsió és
molt feble i no té cap importància. Quan passa per la posició
per la qual tenim ![]() aquesta
força podria ser important i provocar una disminució de
aquesta
força podria ser important i provocar una disminució de![]() i
consegüenment de
i
consegüenment de![]() .
Encara es compliria
.
Encara es compliria![]() ,
però caldrà esbrinar aquesta velocitat. Dit en altres paraules:
negligint l'efecte Joule de les resistències, el sistema conserva l'energia.
Hi ha un transvasament d'energia cap a la bobina, no tota l'energia gravitatòria
es converteix en cinètica. Les pèrdues per efecte Joule compliquen
més aquesta situació. Vegeu la secció
L'efecte magnètic secundari una mica més avall.
,
però caldrà esbrinar aquesta velocitat. Dit en altres paraules:
negligint l'efecte Joule de les resistències, el sistema conserva l'energia.
Hi ha un transvasament d'energia cap a la bobina, no tota l'energia gravitatòria
es converteix en cinètica. Les pèrdues per efecte Joule compliquen
més aquesta situació. Vegeu la secció
L'efecte magnètic secundari una mica més avall.
c) La bobina té un cert gruix, ![]() ,
que no hem tingut en compte perquè complica mot les coses i no introdueix
res de nou en l'aspecte conceptual. En el cas general, si a
és la relació entre el gruix de la bobina i el seu diàmetre,
,
que no hem tingut en compte perquè complica mot les coses i no introdueix
res de nou en l'aspecte conceptual. En el cas general, si a
és la relació entre el gruix de la bobina i el seu diàmetre,
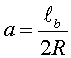 , s'obté
, s'obté 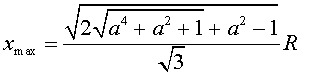 .
Especificarem aquests resultats per al cas de bobina prima
.
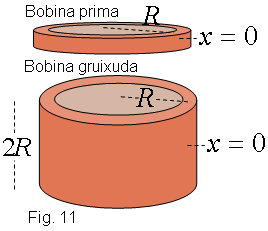
Especificarem aquests resultats per al cas de bobina prima ![]() (a
= 0), i de bobina gruixda
(a
= 0), i de bobina gruixda ![]() (a = 1).
(a = 1).
Bobina prima
|
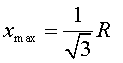 |
(18) |
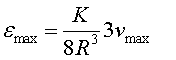 |
(19) |
Bobina gruixuda 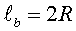
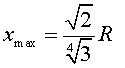 |
(20) |
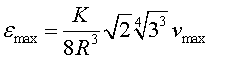 |
(21) |
L'efecte magnètic secundari
Podem fer una avaluació aproximada dels efectes magnètics secundaris
analitzant el terme de correcció del flux causat per l'autoinducció
L de la
bobina, ![]() , que dóna
lloc a un terme de correcció en la força electromotriu,
, que dóna
lloc a un terme de correcció en la força electromotriu, 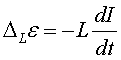 .
Si la resistència total és
.
Si la resistència total és![]() ,
llavors
,
llavors 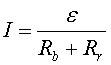 , i així
tenim
, i així
tenim
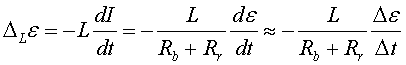 |
(22) |
Si prenem l'interval de temps en què hi ha l'augment de FEM ![]() de 0 fins a
de 0 fins a ![]() ,
podem aproximar
,
podem aproximar 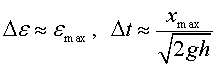 ,
on hem pres
,
on hem pres ![]() com
una mesura del tram de caiguda en què hi ha el creixement efectiu de
fem
com
una mesura del tram de caiguda en què hi ha el creixement efectiu de
fem![]() de 0
fins a
de 0
fins a ![]() . Ara, aproximant
el coeficient d'autoinducció de la bobina pel d'una bobina llarga,
d'una llargada
. Ara, aproximant
el coeficient d'autoinducció de la bobina pel d'una bobina llarga,
d'una llargada ![]() ,
, 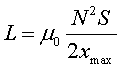 ,
obtenim finalment la importància relativa del terme d'autoinducció
(22) explicitant els paràmetres rellevants
del nostre cas
,
obtenim finalment la importància relativa del terme d'autoinducció
(22) explicitant els paràmetres rellevants
del nostre cas
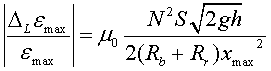 |
(23) |
Finalment com que es tracta d'un càlcul aproximat, podem substituir
![]() pel valor corresponent
a bobina prima. Així l'efecte magnètic secundari serà petit
sempre que
pel valor corresponent
a bobina prima. Així l'efecte magnètic secundari serà petit
sempre que
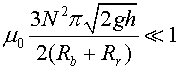 |
(24) |
Podem controlar aquest valor amb la resistència Rr.
En el diseny de l'experiència caldrà controlar aquests efectes, que en general són febles.
Solucions a les qüestions
1) La relació és de proporcionalitat o de linealitat.
2)La relació és de proporcionalitat o de linealitat.
3) El valor del voltatge induït serà més gran però no arribarà a ser el doble.
4) La gràfica que ens surt amb
l’oscil·loscopi seria semblant, però els signes de les pendents
serien just els contraris en cada zona.
5) La proporció entre l’energia potencial gravitatòria i la magnètica seria encara més gran i les suposicions que hem fet encara serien millors.
6) Seria 249,3 m/s
7) Si llancem des de 0,6 m, hauria de tenir 24043 voltes..
8) Serien una eina bàsica per
calcular la potència i l’energia dissipada per la bobina, necessitem
la resistència de la bobina que en el nostre cas és ![]() , i la resistència que tanca el circuit, que és
, i la resistència que tanca el circuit, que és ![]() .
.
9) Podem distingir tres zones al gràfic voltatge /temps. La primera correspon a la fase d’apropament, la segona al canvi de polaritat de l’imant quan travessa la bobina, i la darrera a la fase d’allunyament.
10) Prové de l’energia potencial gravitatòria que va perdent l’imant.
11) A causa de les pèrdues per fregament i de l’energia que s’indueix a la bobina. Les pèrdues per fregament no es recuperen com a cinètica, però les que són causades per la bobina es recuperarien totalment quan l'imant sallunyés per sota si la bobina no tingués resistència i no hi posessim cap resistència més. Amb resistències, la recuperació és parcial.
12) Si el corrent induït fos a
l’inrevés, acceleraria l’imant enlloc de frenar-lo en la
caiguda i tindríem una font inesgotable d’energia.
| Sumari |  3/9 3/9  |
| Inici | ||
| ISSN:
1988-7930 Adreça a la xarxa:
www.RRFisica.cat Adreça electrònica:
redaccio@rrfisica.cat
difusio@rrfisica.cat |
||
  Programació web: Xavier Jaén i Daniel Zaragoza. Correcció lingüística: Serveis Linguïstics de la Universitat Politècnica de Catalunya. |
Aquesta
obra està subjecta a una Llicència de Creative Commons |
|
|
Recursos de Física col·labora amb la baldufa i també amb ciències Revista del Professorat de Ciències de Primària i Secundària (Edita: CRECIM-UAB) |
||


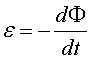
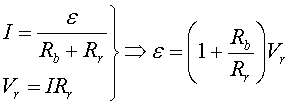
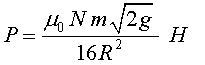

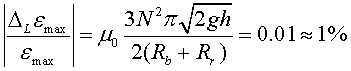


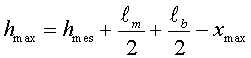
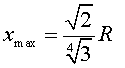 ).
També tabulem la velocitat corresponent a cada altura. La taula
que en resulta és:
).
També tabulem la velocitat corresponent a cada altura. La taula
que en resulta és: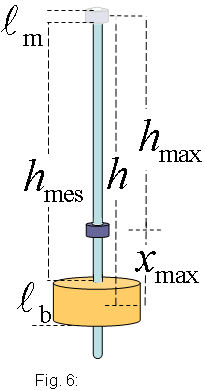
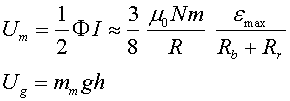
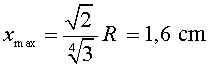 .
.