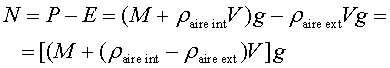IntroduccióTots sabem que l'aire pesa i tenim ben incorporat el concepte de pressió atmosfèrica; però si volem pesar l'aire que hi ha dins d'un recipient possiblement no sabrem com fer-ho.
Com que la pilota és un recipient tancat, sembla que hauríem de poder determinar el pes de l'aire que hi ha a l'interior calculant la diferència de pes entre la pilota inflada i la pilota buida. Les pilotes estan inflades a sobrepressió respecte de la pressió atmosfèrica, però la diferència de pes entre quan està inflada i quan està buida no correspon a tot l'aire que hi ha a dins.
En analitzar les forces que actuen sobre la pilota quan l'estem pesant, trobarem la força normal i la força d'empenyiment. En la solució es demostra que aquestes forces s'anul·len quan la densitat de l'aire interior és igual a l'exterior, cosa que justifica per què la balança no detecta l'aire interior quan aquest està en equilibri amb la pressió atmosfèrica. Guia del professorat 
Guia de l'alumnat
Material
- Pilota amb forat per a la vàlvula
|
 |
|
 |
|
 |
|
 |
Procediment i qüestions
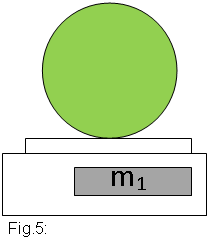
| 1) Inflem la pilota a pressió.
Traiem la vàlvula i la deixem al plat de la balança, juntament
amb la pilota. Ho pesem (vegeu la figura 5).
m1 ( pilota + aire a pressió
+ vàlvula) =
2) Introduïm la vàlvula
a la pilota i deixem escapar aire fins que no en surti més. En
aquest punt l'aire interior està en equilibri amb la pressió
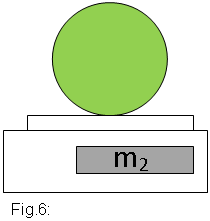
atmosfèrica. Ho pesem (vegeu la figura 6).
m2( pilota + aire a pressió atmosfèrica
+ vàlvula) =
- Justifica la diferència entre les dues pesades.
- Quant d'aire ha sortit de la pilota?
- Quant d'aire ha quedat dins la pilota?
- Mesura, de forma aproximada, el radi de la pilota en aquest equilibri
: R =
|
 |
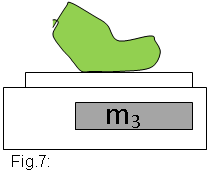
| 3) Pressionem amb les mans
la pilota per treure’n més aire fins que en quedi aproximadament
la meitat (en volum). La tornem a pesar sense treure-hi la vàlvula
(vegeu la figura 7).
m3 ( pilota + 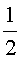 d'aire + vàlvula) =
d'aire + vàlvula) =
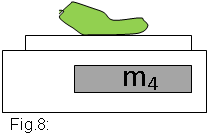
4) Finalment fem sortir tot l'aire
de la pilota i, sense treure’n la vàlvula, la tornem a pesar
(vegeu la figura 8).
m4 ( pilota + vàlvula) =
5) Comenta els resultats de les
quatre pesades
|
 |
| 6) El resultat de cada pesada
té a veure amb tres forces que actuen sobre la pilota quan és
sobre la balança. Pots identificar-les?
7) Per a la situació 2
en què hi ha equilibri amb la pressió atmosfèrica,
calcula:
- • El volum d'aire que hi ha a la pilota.
- La massa d'aire que hi ha dins la pilota. La densitat de l'aire en
condicions normals és:
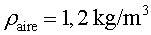
- Com encaixa aquesta massa en les pesades que s'han fet?
|
 |
Solucions
Resultats de les pesades:
m1 ( pilota + aire a pressió + vàlvula)
= 499,1 g
m2( pilota + aire a pressió atmosfèrica
+ vàlvula) = 493,9 g
m3 ( pilota + 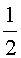 d'aire + vàlvula) = 493,9
g
d'aire + vàlvula) = 493,9
g
m4 ( pilota + vàlvula) = 493,9
g
m2< m1
perquè ha sortit aire de la pilota que estava a pressió. A dins
de la pilota ha quedat l’aire que pot contenir en equilibri amb la pressió
atmosfèrica exterior, és a dir un volum igual al que desplaçaria
la pilota.
Volum i massa d’aire a dins de la pilota en equilibri amb la pressió
atmosfèrica.
El perímetre ens dóna 68,6
cm; així que el radi exterior serà R
= 10,9 cm.
Per al radi interior agafarem el valor aproximat de 10,5
cm.
El volum i la massa de l’aire interior en equilibri serien, si la densitat
de l’aire en condicions normals és d’1,2
kg/m3:
volum = 4,8·10-3
m3 massa 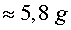
Aquesta massa no es detecta en cap de les pesades. Només podem pesar
l’excés d’aire a pressió que hi havia a l’inici,
però no podem calcular-ne el volum perquè la densitat és
diferent.
| Inici |
|
|
| ISSN:
1988-7930 Adreça a la xarxa:
www.RRFisica.cat Adreça electrònica:
redaccio@rrfisica.cat
difusio@rrfisica.cat
Comitè de redacció : Josep Ametlla, Octavi
Casellas, Xavier Jaén, Gemma Montanyà, Cristina Periago,
Octavi Plana, Jaume Pont i Ramon Sala.
Treballem conjuntament : Societat Catalana de Física,
Associació de Professores i Professors de Física i Química
de Catalunya,XTEC, Universitat Politècnica de Catalunya, Universitat
de Barcelona
|
   
Programació web: Xavier Jaén i Daniel Zaragoza.
Correcció lingüística: Serveis Linguïstics
de la Universitat Politècnica de Catalunya. |
Aquesta
obra està subjecta a una
Llicència
de Creative Commons

|
|
Recursos
de Física col·labora amb la
baldufa i també amb ciències
Revista del Professorat de Ciències de Primària i Secundària
(Edita: CRECIM-UAB)
|
|
|

 6/9
6/9