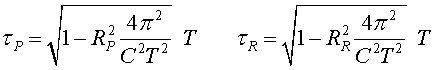 
El tercer bessó
Introducció
En el número anterior, en relació amb la llei
de Faraday, acabàvem dient: "Einstein i la relativitat
acabaran d'arreglar el que s'ha d'entendre exactament per sistema de referència
inercial, però això és tota una altra història".
Avui toca una mica d'aquesta altra història. El problema que ens ocupa
és conegut com a paradoxa dels bessons. Començarem de ple explicant
en què consisteix i on és el fet ( aparentment) paradoxal.
Els bessons
La història comença amb dos bessons, en Pere
(amb samarreta verda) i en Ramon (amb samarreta vermella). Sempre han
viscut junts i avui és el seu aniversari. Tenen una edat de 12
anys exactament. Cap problema. A la figura 1 tenim en Pere i en Ramon
residents fixos en algun poble de la Terra.
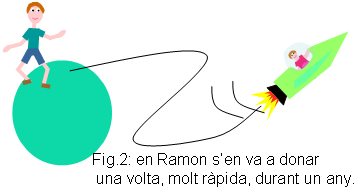
Aquest mateix dia en Ramon s'enfila en una nau i se'n va a fer un tomb
per l'univers a gran velocitat (figura 2). Al cap de 6 mesos de viatge
gira cua i comença el retorn cap a la Terra (figura 3). En arribar
a la Terra els dos bessons comproven amb gran sorpresa que tenen edats
molt diferents. En Ramon té 13 anys, és a dir ha estat,
segons ell, un any viatjant pel cel. En canvi en Pere ja és un
home vell (figura 4). No és que hagi envellit en un any. Ell ha
viscut tots els any en plenitud juntament amb la resta d'habitants del
planeta.
Fins aquí pot semblar sorprenent, però no hi ha cap paradoxa,
no és ciència ficció ni res de res de tot això.
Efectivament la teoria de la relativitat preveu que passi així...
i així passa! La comprovació ja és clàssica
i es fa amb rellotges atòmics (la paraula atòmic només
vol ressaltar que es tracta d'aparells de gran precisió). Dos rellotges,
A
i B,
es posen exactament a l'hora en un mateix lloc. A un d'ells, el B,
se li fa donar un tomb en un avió prou ràpid. En tornar
es comprova que el rellotge B
va amb retard respecte de l'A.
Fem notar que si els rellotges fossin encara més precisos podríem
fer la comprovació utilitzant un cotxe (o fins i tot una bicicleta)
en lloc d'un avió. És a dir, aquí els coets i l'espai
llunyà no hi tenen un paper especialment rellevant. Ajuden, això
sí, a fer-ho tot plegat un pèl més màgic.
El fet important és que cal que el que viatja ho faci a gran velocitat...
i que torni! |
 |
 |
 |
La paradoxa
Ara ens fixarem en la paradoxa. Tinguem en compte que la paradoxa apareix
perquè algú ens marca un gol. Bé, deixem que ens
facin el gol, després ja ens venjarem.
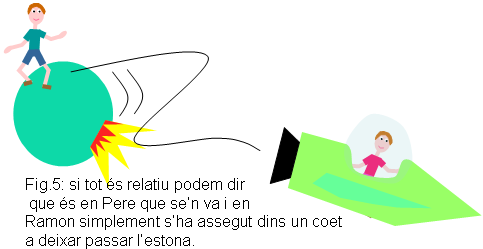
Segons la relativitat el moviment és relatiu, per tant, és
el mateix que pensem que en Ramon viatja respecte d'en Pere en coet com
que és en Pere qui se'n va de viatge respecte d'en Ramon, això
sí, juntament amb tota la Terra (figura 5). Així podem aplicar
el mateix raonament que fa la relativitat i arribar a la conclusió
que quan es tornin a trobar serà en Ramon el vell, mentre que en
Pere tindrà només 13 anyets. La paradoxa està servida! |
 |
|
 |
La relativitat
El gran mèrit d'Albert Einstein és haver
fet les coses simples. Fem, doncs, les coses simples. Comencem des del
principi de tot. Som tots nens i ens fem moltes preguntes. De fet, ho
preguntem tot. No deixem passar res. I no admetem respostes per sortir
del pas!
Si volem parlar de temps i espai necessitarem saber com
es mesuren aquestes magnituds.
Distàncies/regle: per mesurar
una distància entre dos punts quiets juxtaposem un regle patró
i comptem les divisions que caben entre els punts.
Temps/Rellotge: per mesurar un temps
entre dos esdeveniments que ocorren al mateix lloc comptem el nombre d'oscil·lacions
d'un rellotge patró (situat en aquest lloc) que caben entre els
dos esdeveniments.
|
 |
En tenim prou amb això? Hem parlat de distàncies
entre punts quiets i intervals temporals entre esdeveniments que ocorren
al mateix lloc. Necessitem poder parlar de distàncies entre punts
que es mouen i d'intervals de temps entre esdeveniments que ocorren en
llocs diferents. El que necessitem en definitiva és un sistema
de referència: utilitzem el nostre regle per anar assignant
a cada punt de l'espai fix respecte nosaltres, ara ja convertits en observadors,
una etiqueta que identifiqui la seva posició. També deixarem
a cada punt de l'espai un rellotge idèntic al rellotge patró.
Un cop fet això... cal posar a l'hora els rellotges! És
a dir, cal sincronitzar els rellotges situats en diferents
punts de l'espai. Un cop tinguem tots els rellotges sincronitzats podrem,
per exemple, caracteritzar la trajectòria del coet d'en Ramon anotant
les etiquetes dels punts per on passa i la lectura de cada rellotge de
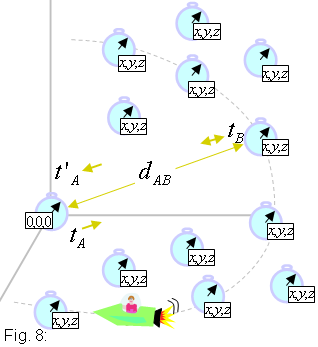
cada punt en l'instant que hi passa. L'aspecte de l'espai-temps d'un observador
és representat a la figura 8.
Hom podria pensar que això és una bestiesa,
que podem posar a l'hora els rellotges quan els fabriquem tots al mateix
lloc i després ja els anirem repartint cap aquí i cap allà
en un viatge per l'espai...Bé, potser seria una possibilitat, però
recordem què passa amb els bessons! Viatjar no és un fenomen
senzill! Haurem de precisar com és aquest viatje etc i la cosa
potser se'ns embolica. Penseu en agafar un rellotge de pèndol (o
de molla) i anar-lo accelerant i frenant amunt i avall... quin desastre!.
Així que farem tal com va fer Albert Einstein en el seu famós
article del 1905. Part de la primera pàgina original es pot veure
a la figura 9. |
 |
A la figura 10 podeu veure un paràgraf de la versió
anglesa de l'article. Noteu que el que hi diu i el que diem nosaltres
és molt semblant... cosa de nens.
Tenim repartits els diferents relloges per l'espai, encara
per sincronitzar. És a dir si la lectura del nostre rellotge patró
A,
situat a (0,0,0)
és tA
, quina ha de ser la lectura d'un rellotge B
situat a (x,y,z)?
Si ens podem comunicar instantàniament amb B
des de A
llavors diriem, sense més, que en l'instant en què A
marca tA
, tB=
tA . Però això no és possible
i la física es construeix a base de coses possibles. Bé,
doncs establim un sistema de comunicació que vagi a una velocitat
C.
Ep, encara no ens sentim obligats que aquesta velocitat sigui la de la
llum. C
és simplement una velocitat d'un possible sistema de comunicació.
Tant ens fa que sigui 30km/h
com 30000km/h...
o la velocitatde la llum. En podem dir protocol de sincronització-C
(PS-C).
Si en el temps tA
enviem un senyal de A
a cap a B
que arriba a B
en el temps tB
i surt de B
(portant la informació tB)
per arribar a A
en el temps t'A
, direm que A
i
B estan sincronitzats si
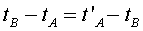 . A la figura 8 podeu veure representat aquest protocol de sincronització.
Així, si la velocitat a la qual ens comuniquem és C
i dAB
és la distància que hi ha entre A
i B
, tindrem
. A la figura 8 podeu veure representat aquest protocol de sincronització.
Així, si la velocitat a la qual ens comuniquem és C
i dAB
és la distància que hi ha entre A
i B
, tindrem
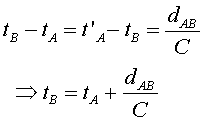
Insistim que C
no té perquè ser la velocitat de la llum, això
vindrà una mica més endavant.
|


|
Principi de relativitat i sistemes de referència inercials
Un cop tenim clar el que és un
sistema de referència, podrem escriure les expressions matemàtiques
corresponents a la nostra teoria en el nostre sistema de referència.
Haurem d'admetre que no som els únics capacitats per construir
un sistema de referència. Qualsevol observador, sigui on sigui,
es mogui o no repecte de nosaltres, pot fer el mateix. El que sí
que demanem és que faci servir el mateix protocol de sincronització
PS-C.
La velocitat de la comunicació no pot ser diferent per a cada observador.
L'experiència ens indica que les causes del moviment dels cossos
és la mateixa per a sistemes que es mouen els uns respecte dels
altres amb velocitat constant. Aquest fet s'eleva a la categoria de principi.
Principi de relativitat: Observadors en
llocs diferents, temps diferents, orientacions i que es mouen els uns
respecte dels altres a una velocitat constant no notaran cap canvi en
les lleis de la natura.
Hom diu que les lleis de la natura són forma-invariant
o covariants respecte de translacions espacials,
temporals, rotacions i transformacions de velocitat.
Classifiquem tots els sistemes de referència en diferents
conjunts de sistemes de referència inercials (SRI).
Dins de cada classe els SRI es mouen amb velocitats relatives constants.
Privilegiar un conjunt respecte dels altres és una qüestió
complicada i molts cops depen del grau de precisió amb què
treballem. En línies generals podem considerar que la Terra és
un SRI i prendre la classe associada. Si afinem més, prendrem el
Sol com a SRI, la nostra galàxia...el cúmul local...etc.
Aquesta multiplicitat de classes d'SRI ja va preocupar Newton. Einstein
també era conscient del problema, però va haver d'esperar
uns anys i fer una altra revolució (la relativitat general) per
solucionar aquest detall.
|
 |
Ens situem en una classe d'SRI, per exemple el cas que la Terra
n'és un. Un mateix esdeveniment P
pot ser observat des de desde dos SRI diferents, S
i S'. 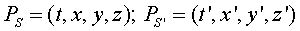 .
Quina relació hi ha entre aquestes coordenades? No és dificil
trobar la resposta, ara que tenim els rellotges ben sincronitzats. La solució
es basa, modernament, en el principi de relativitat i en hipòtesis molt
generals d'homogeneïtat i isotropia de l'espai-temps, sense fer cap esment
de la velocitat de la llum! .
Quina relació hi ha entre aquestes coordenades? No és dificil
trobar la resposta, ara que tenim els rellotges ben sincronitzats. La solució
es basa, modernament, en el principi de relativitat i en hipòtesis molt
generals d'homogeneïtat i isotropia de l'espai-temps, sense fer cap esment
de la velocitat de la llum!
Més difícil és fer una interpretació
útil del resultat. Ara ens ocuparem d'això. Si algú ens
pregunta què és una rotació i com a resposta li donem l'expressió
d'una matriu plena de sinus i cosinus, el més probable és que
el nostre interlocutor pensi que li prenem el pèl. En canvi si li diem
que es tracta de transformacions de punts que deixa invariant
la distància relativa entre ells, el nostre interlocutor potser entendrà
alguna cosa, o com a mínim la conversa podrà continuar. Mirem,
doncs, de continuar. La distància entre dos punts molt pròxims
situats en un lloc qualsevol es pot escriure 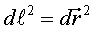 ,
on hem utilitzat la notació ,
on hem utilitzat la notació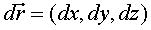 .
Que les rotacions deixin invariant la distància vol dir que .
Que les rotacions deixin invariant la distància vol dir que 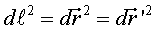 . .
Un esdeveniment és alguna cosa més que un
punt a l'espai. És quelcom que passa en un punt i en un instant.
La diferència entre dos esdeveniments molt pròxims és
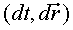 . Doncs bé,
no és difícil demostrar que podem interpretar les transformacions
entre dos SRI que utilitzen PS-C
com les que deixen invariant les quantitats . Doncs bé,
no és difícil demostrar que podem interpretar les transformacions
entre dos SRI que utilitzen PS-C
com les que deixen invariant les quantitats 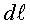 i i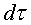 , ,
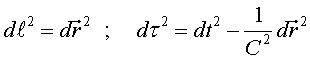 (1)
(1)
Aquí 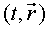 són
les coordenades temps-espai d'un esdeveniment respecte d'un sistema inercial
S
qualsevol. Les transformacions inclouen translacions i rotacions (independents
del temps) i translacions temporals com en el cas no relativista. El que
són diferents són les transformacions de velocitat. són
les coordenades temps-espai d'un esdeveniment respecte d'un sistema inercial
S
qualsevol. Les transformacions inclouen translacions i rotacions (independents
del temps) i translacions temporals com en el cas no relativista. El que
són diferents són les transformacions de velocitat.
|
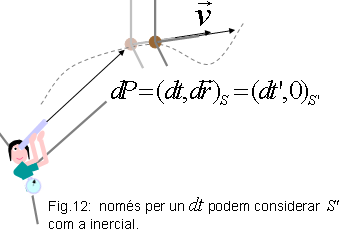 |
Temps propi
Ara considerem S
un observador inercial qualsevol i, encara que només sigui per uns instants,
S' es mou
amb l'objecte observat, com a la figura 12. S'és
instàntaniament inercial. Tindrem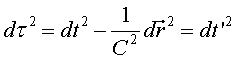 .
Però .
Però 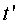 és
el temps de S',
és a dir, el temps propi de l'objecte. Així,
pel fet que és
el temps de S',
és a dir, el temps propi de l'objecte. Així,
pel fet que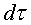 és
invariant, podem interpretat aquesta mena de distància espai-temporal és
invariant, podem interpretat aquesta mena de distància espai-temporal
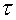 com el temps propi
de l'objecte observat. Si l'observador S
deixa passar una estona, per exemple, de 0
a t, el
temps propi que ha transcorregut per a l'objecte, de 0
a com el temps propi
de l'objecte observat. Si l'observador S
deixa passar una estona, per exemple, de 0
a t, el
temps propi que ha transcorregut per a l'objecte, de 0
a 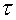 , es pot obtenir integrant
l'expressió (1) , es pot obtenir integrant
l'expressió (1)
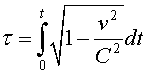 (2) (2)
La llum
Recordeu que encara no hem dit res de la velocitat de la llum.
Estem utilitzant el PS-C,
on C és
la velocitat del nostre sistema de comunicació. Segons l'expressió
(2), si l'objecte anés a la velocitat C
no li passaria el temps i si superés aquesta velocitat... ens quedem
sense resposta? Hi ha una sortida: que el protocol de sincronització
es faci a una velocitat a la qual no pugui arribar cap objecte material, és
a dir fer-lo a una velocita que sigui la màxima velocitat existent. Bé,
doncs així ho farem. La qüestió ara és si hi ha un
límit o no per a les velocitats. Si no n'hi ha podrem fer servir PS-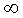 .
Així és com es procedeix en la mecànica no relativista.
Si .
Així és com es procedeix en la mecànica no relativista.
Si 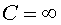 , segons (1)
les transformacions entre dos sistemes de referència serien les que deixen
invariants , segons (1)
les transformacions entre dos sistemes de referència serien les que deixen
invariants
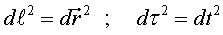 (3) (3)
i les transformacions de velocitat esdevindrien 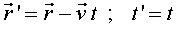 ,
és a dir, es tractaria de les transformacions de Galileu usuals. També
amb ,
és a dir, es tractaria de les transformacions de Galileu usuals. També
amb 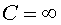 de (2),
obtenim de (2),
obtenim 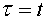 i tot l'embolic
del temps deixa d'existir. Però l'experiència sembla indicar que
hi ha efectivament un límit: la velocitat màxima que s'ha trobat
fins ara coincideix amb la velocitat de la llum en el buit.
Podem enunciar aquest fet com a principi. i tot l'embolic
del temps deixa d'existir. Però l'experiència sembla indicar que
hi ha efectivament un límit: la velocitat màxima que s'ha trobat
fins ara coincideix amb la velocitat de la llum en el buit.
Podem enunciar aquest fet com a principi.
Principi de la velocitat límit: existeix
una velocitat màxima que cap objecte pot superar. El seu valor és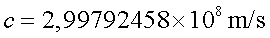 . .
Així, el que cal és fer servir el protocol de sincronització
PS-c , no
cal que sigui "llum", n'hi ha prou que sigui un sistema de comunicació
possible i que vagi sempre a la mateixa velocitat 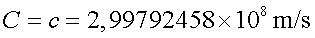 Així tot quadra.
Així tot quadra.
Solució de la paradoxa
Apliquem els nostres coneixements al viatges dels bessons.
Ara que veiem la importància de l'SRI, de seguida veiem que només
el bessó que no viatja és inercial. El bessó viatger
necessita accelerar per començar el seu viatje, frenar i tornar
a accelerar per poder tornar i finalment frenar per arribar a estar amb
el seu germà...Si apliquem (2) amb un S
que sigui en Pere com a observador d'en Ramon, veiem clarament que és
en Ramon qui en tornar és més jove que en Pere. I no ho
podem fer al revés: en Ramon no pot ser un observador inercial.
Per veure-ho més clar podem introduir un tercer bessó, en
Martí, que sempre s'estigui quiet a la Terra com a observador inercial
imparcial.
Considerem la situació més general en què
tant en Pere com en Ramon se'n van de viatge, un viatge circular durant
el mateix període de temps (segons en Martí!), 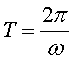 . .
|
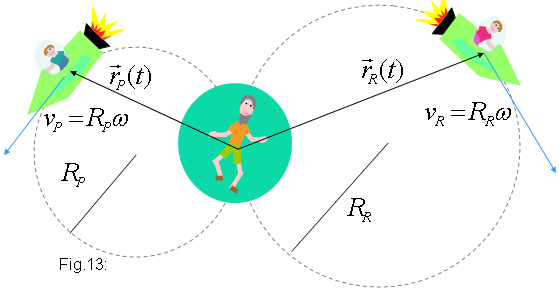 |
Les velocitats poden ser diferents perquè els radis ho
són. Amb subíndex P
i R segons
si es tracta d'en Pere o d'en Ramon, hem representat la situació a la
figura 13. És en Martí qui fa els càlculs amb les seves
dades referides als seus germans per igual. Li surt, aplicant (2)
a cada un d'ells
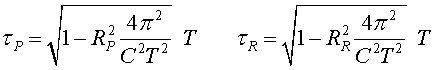
així qui fa el viatge a més velocitat (diguem en
Ramon) durant el mateix temps és qui esdevé més jove: 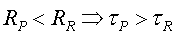 .
Un cas particular és no viatjar .
Un cas particular és no viatjar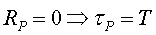 .
El gol que ens han marcat és haver utilitzat la famosa frase "tot
és relatiu", que s'hauria de canviar o precisar com a "tot
és relatiu al sistema de referència inercial",
és a dir: no tot és relatiu. .
El gol que ens han marcat és haver utilitzat la famosa frase "tot
és relatiu", que s'hauria de canviar o precisar com a "tot
és relatiu al sistema de referència inercial",
és a dir: no tot és relatiu.
Postdata
Per acabar posem-hi una mica d'obscuritat. En El
racó obscur del número 2 d'aquesta revista parlàvem
de les forces d'inèrcia. En concret, ens interessa la secció que
deia Caic lliurement. Quan caiem lliurement, com
en un camp gravitatori constant, o sempre que totes les parts del nostre
cos estiguin sotmeses a la mateixa acceleració, no notem res:
ens sembla que estem quiets o, si sabem una mica de física, viatjan en
moviment uniforme. De fet, això és el que fan els astronautes
en els entrenaments. Es deixen caure dins d'un avió i els sembla que
estan en absència de gravetat.
Els sistemes de referència associats a aquests moviments també
tenen tot el dret a ser inercials pel fet que no els podem distingir de forma
intrínseca els uns dels altres. Dit d'una altra manera, en referència
a la secció Principi de relativitat i sistemes
de referència inercials, totes les classes de sistemes de referència
han de ser igual de vàlides per "fer física". L'espai-temps
no és absolut. Per resoldre això, Einstein va haver d'edificar
tota una altra teoria: la relativitat general. Però ara sí que
entraríem en tota una altra història!
| Inici |
|
|
| ISSN:
1988-7930 Adreça a la xarxa:
www.RRFisica.cat Adreça electrònica:
redaccio@rrfisica.cat
difusio@rrfisica.cat
Comitè de redacció : Josep Ametlla, Octavi
Casellas, Xavier Jaén, Gemma Montanyà, Cristina Periago,
Octavi Plana, Jaume Pont i Ramon Sala.
Treballem conjuntament : Societat Catalana de Física,
Associació de Professores i Professors de Física i Química
de Catalunya,XTEC, Universitat Politècnica de Catalunya, Universitat
de Barcelona
|
   
Programació web: Xavier Jaén i Daniel Zaragoza.
Correcció lingüística: Serveis Linguïstics
de la Universitat Politècnica de Catalunya. |
Aquesta
obra està subjecta a una
Llicència
de Creative Commons

|
|
Recursos
de Física col·labora amb la
baldufa i també amb ciències
Revista del Professorat de Ciències de Primària i Secundària
(Edita: CRECIM-UAB)
|
|
|

 8/9
8/9 









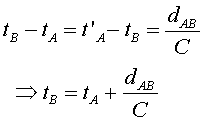



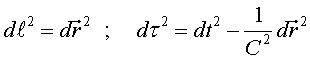 (1)
(1)
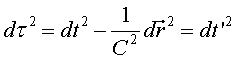 .
Però
.
Però 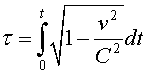 (2)
(2)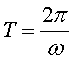 .
.