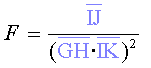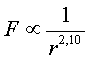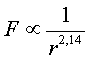IntroduccióQuin tipus de força fa que un planeta descrigui una òrbita el·líptica? En general, hi ha poques experiències relacionades amb la llei de la gravitació universal que es portin a terme amb l'alumnat de secundària i que suposin efectuar algun tipus de mesura. A continuació, proposem una experiència que es pot presentar a l'alumnat de diferents maneres. La idea original apareix a la la revista The Physics Teacher de gener de 2007, a l’article de Prentis et al. [1]. En essència, es tracta d'una adaptació de la fórmula del corol·lari 5 de la proposició VI del llibre I dels Principis matemàtics de filosofia natural de Newton i les aplicacions subsegüents dels problemes VI, VII i VIII (o proposicions XI, XII, XIII).
Guia del professorat
Antecedents històrics
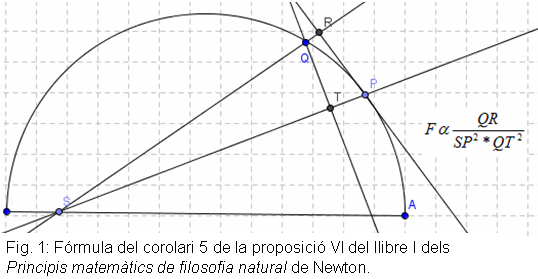
Al corolari 5 de la proposició VI del llibre I dels
Principis matemàtics de filosofia natural, Newton demostra que
si un cos es mou segons la trajectòria  (vegeu la figura 1) i S
és el punt cap a on es dirigeix la força centrípeta, aquesta
es inversament proporcional a:
(vegeu la figura 1) i S
és el punt cap a on es dirigeix la força centrípeta, aquesta
es inversament proporcional a:
O bé d’una altra manera
A continuació, Newton demostra que:
- Si la trajectòria d'un cos és una el·lipse i la força
va dirigida cap a un dels focus, aleshores aquesta força és
inversament proporcional al quadrat de la distància (proposició
XII, problema VI).
- Si la trajectòria d'un cos és una hipèrbola i la força
va sempre dirigida cap a un dels focus, aleshores és inversament proporcional
al quadrat de la distància (proposició XII, problema VII).
- Si la trajectòria d'un cos és una paràbola i la força
va dirigida cap al focus, aleshores és inversament proporcional al
quadrat de la distància (proposició XIII, problema VIII).
Deducció moderna de la fórmula de Newton
Les demostracions dels Principia mathematica són geomètriques
i molt difícils de seguir; a continuació, justifiquem la fórmula
de Newton (1) amb un llenguatge i una notació més adaptada al
nostre temps.
Considerem un planeta que giri al voltant del Sol, punt G
amb una trajectòria no especificada (la figura 2 correspon al cas de
trajectòria el·líptica). En un determinat interval de temps
es mou del punt H
al punt I.
Si no hi hagués cap força sobre el planeta, d’acord amb
la llei de la inèrcia de Galileu, el planeta es mouria segons la línia
tangent  , amb la velocitat
constant que tenia a H. , amb la velocitat
constant que tenia a H.
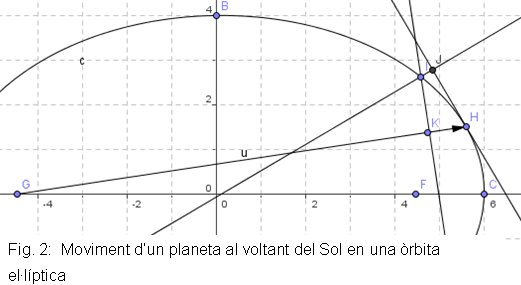
La desviació  ens proporciona una mesura de la força. En una primera aproximació,
més certa com més pròxims sigui la distància
ens proporciona una mesura de la força. En una primera aproximació,
més certa com més pròxims sigui la distància ,
podem pensar que el planeta experimenta una caiguda lliure amb acceleració
constant a,
és a dir: ,
podem pensar que el planeta experimenta una caiguda lliure amb acceleració
constant a,
és a dir:
A la segona llei de la dinàmica, F=ma
, substituïm l’acceleració pel valor que s'obté d'aïllar-la
de (2):
o d’una altra manera,
Si ara utilitzem la segona llei de Kepler, el radi vector que connecta el Sol
amb el planeta escombra àrees iguals en intervals de temps iguals, per
la qual cosa tenim 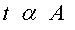 , i
en conseqüència: , i
en conseqüència:
Cal que recordem que el compliment de la segona llei de Kepler ( que equival
a la conservació del moment angular) no suposa que la força sigui
del tipus 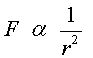 , n'hi ha prou
que es tracti d'una força central. , n'hi ha prou
que es tracti d'una força central.
Quan tenim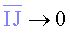 o o 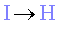 ,
podem aproximar l’àrea del sector escombrat pel radi vector ,
podem aproximar l’àrea del sector escombrat pel radi vector  per l’àrea del triangle
per l’àrea del triangle 
I finalment si substituïm (6) a (5), obtenim que:
és a dir, tenint en compte els canvis de notació, obtenim (1).
S’ha de fer notar a l'alumnat que en l’expressió (7), si
prescindim de la constant de proporcionalitat, la força que actua sobre
el planeta té unitats de 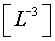 .
També que en la deducció anterior no s'ha utilitzat enlloc que
la trajectòria sigui justament una el·lipse. Ara es tracta precisament
de fer servir (7) per veure que, si es tracta d'una el·lipsi
resulta .
També que en la deducció anterior no s'ha utilitzat enlloc que
la trajectòria sigui justament una el·lipse. Ara es tracta precisament
de fer servir (7) per veure que, si es tracta d'una el·lipsi
resulta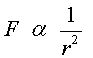 !. !.
L'expressió (7) pot ser explicada a l'estudiantat de batxillerat sense
gaires problemes.A partir d'aquest punt, suposarem que l'estudiantat coneix
aquesta expressió.El procediment general de dibuixar una el·lipse
i dur a terme les mesures corresponents es pot fer amb programari lliure. Un
bon programa és:
De tota manera, amb precissió suficient es pot fer el mateix dibuixant
(no virtualment) una el·lipse força gran. A la fitxa de l'estudiantat
no suposarem necessariament l'existència de cap programa.
Un cop tenim les mesures , ,
 i i  (per
a una col·lecció de puntsHi
) podem calcular (per
a una col·lecció de puntsHi
) podem calcular  ( en
unitats ( en
unitats 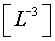 ) i fer la gràfica
d'aquesta quantitat enfront de ) i fer la gràfica
d'aquesta quantitat enfront de 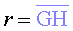 .
Finalment, cal ajustar aquesta gràfica a una corba del tipus .
Finalment, cal ajustar aquesta gràfica a una corba del tipus 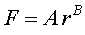 ,
on caldrà trobar els paràmetres A
i B.
Això es pot fer també amb el programari lliure: ,
on caldrà trobar els paràmetres A
i B.
Això es pot fer també amb el programari lliure:
També podem fer servir el programa no gratuit:
És cert que no hi ha una alternativa manual raonable per fer l'ajust.
A la fitxa de l'estudiantat es detallen aquests procediments amb més
profunditat.
Fitxa de l'estudiantat
Objectiu
Mesurar els paràmetres  , ,
 i i  en diferents punts d’una el·lipse, una paràbola o una hipèrbola
i aplicar la fórmula
en diferents punts d’una el·lipse, una paràbola o una hipèrbola
i aplicar la fórmula 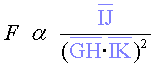 per trobar la llei de la força a la qual està sotmès un
cos que es mou segons aquest tipus de trajectòries.
per trobar la llei de la força a la qual està sotmès un
cos que es mou segons aquest tipus de trajectòries.
1) Amb el programa GeoGebra:
dibuixem una el·lipse de, per exemple, a=6
unitats de semieix major i b=4
unitats de semieix menor, amb el mètode dels 5
punts.
1') Sense el programa:
dibuixem una el·lipse sobre una cartolina prou gran utilitzant
la condició: la suma de les distàncies d'un punt qualsevol
de la el·lipse als focus es manté constant. Escollim els
focus G
i F
convenienment.
2) Amb el programa GeoGebra:
cal determinar els focus G
i Fde
l’el·lipse; la distància del centre de l’el·lipse
als focus és:
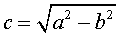
2') Sense el programa:
ja tenim els focus determinats per construcció ( en el pas 1'
hem escollit uns focus)
|

Fig. 4 |
|
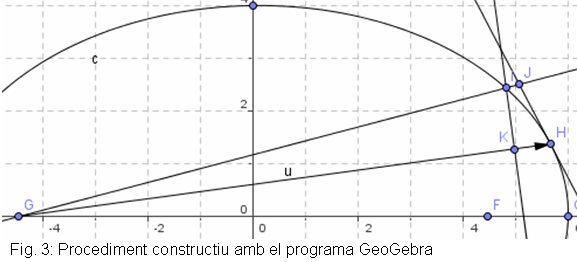
3) Decidim en quin dels focus
situem el Sol, en el nostre cas G
(vegeu la figura 3). Assenyalem un punt H
a l’el·lipse
|

Fig. 5 |
| 4) Dibuixem la tangent a l’el·lipse
que passa pel punt H. |

Fig. 6 |
5) Assenyalem un altre punt
I
a l’el·lipse que sigui proper a H
i dibuixem la recta que passa per G
i H.
|
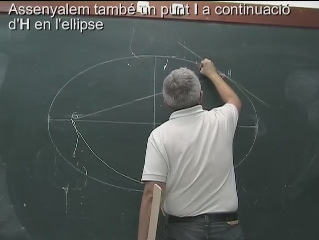
Fig. 7 |
6) La recta que passa per G
i H
talla la recta tangent a l’el·lipse que passa per H
en el punt J.
7) Dibuixem la perpendicular a
 que passa per
I
i que talla a que passa per
I
i que talla a  en el punt K.
en el punt K.
|

Fig. 8 |
8) Ara, mesurem del les distàncies
 , ,  , ,
 per avaluar la
força mitjançant l’expressió: per avaluar la
força mitjançant l’expressió:
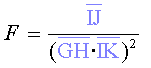
|

Fig. 9 |
9) Repetim els passos de 4
a 8 per diferents
punts Hi
de l’el·lipse.
|

Fig. 10 |
10) Utilitzem el programari
adequat per representar la força obtinguda F
en funció de la distància 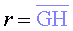
11) Utilitzem el programari adequat
per ajustar aquesta gràfica a una corba del tipus 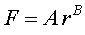 ,
en que caldrà trobar-hi els paràmetres A
i B. ,
en que caldrà trobar-hi els paràmetres A
i B.
12) Opcionalment, es pot repetir
el procediment per a trajectòries parabòliques o hiperbòliques.
|

Fig. 11 |
Solucions
El·lipse
A la taula 1 es recullen els valors de  , ,
 , ,  (mesurats amb el programa GeoGebra) en una el·lipse d'exemple. Les unitats
(u) són convencionals.
(mesurats amb el programa GeoGebra) en una el·lipse d'exemple. Les unitats
(u) són convencionals.
 (u)
(u) |
 (u) (u) |
 =r
(u) =r
(u) |
F (u-3) |
| 0,291 |
1,220 |
10,467 |
0,00178 |
| 0,281 |
1,203 |
10,359 |
0,00181 |
| 0,277 |
1,179 |
9,928 |
0,00202 |
| 0,275 |
1,174 |
9,719 |
0,00211 |
| 0,259 |
1,153 |
9,010 |
0,00240 |
| 0,281 |
1,164 |
8,248 |
0,00305 |
| 0,288 |
1,161 |
7,495 |
0,00380 |
| 0,268 |
1,139 |
6,740 |
0,00445 |
| 0,274 |
1,135 |
5,996 |
0,00592 |
| 0,261 |
1,117 |
5,254 |
0,00758 |
| 0,260 |
1,104 |
4,468 |
0,01069 |
| Taula 1: Relació entre força i distància
al focus de l’el·lipse |
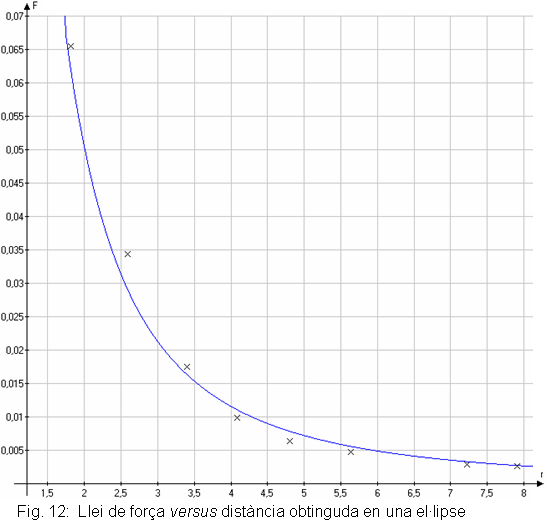
| Si representem gràficament la força
en funció de la distància amb un programari científicogràfic
i utilitzem l’opció que permet ajustar els punts experimentals
a la millor corba, obtenim una llei de dependència entre força
i distància proporcional a l’invers de la distància
al quadrat amb una molt bona aproximació (vegeu la figura 12):
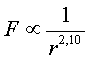
|
 |
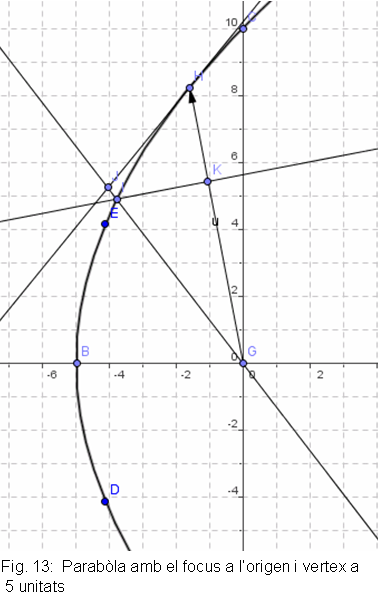
Paràbola
| Si repetim el procediment per una paràbola
(figura 13), també obtenim el mateix tipus de llei .
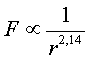
. |
 |
A la taula 2 es recullen els valors de  , ,
 , ,  (mesurats amb el programa GeoGebra) en una paràbola d'exemple. Les unitats
(u) són convencionals.
(mesurats amb el programa GeoGebra) en una paràbola d'exemple. Les unitats
(u) són convencionals.
 (u)
(u) |
 (u) (u) |
 =r
(u) =r
(u) |
F (u-3) |
| 0,471 |
2,971 |
22,033 |
0,00011 |
| 0,456 |
2,940 |
19,687 |
0,00013 |
| 0,445 |
2,933 |
17,994 |
0,00016 |
| 0,428 |
2,905 |
15,879 |
0,00020 |
| 0,433 |
2,885 |
13,918 |
0,00027 |
| 0,420 |
2,847 |
12,199 |
0,00035 |
| 0,443 |
2,823 |
10,017 |
0,00055 |
| 0,447 |
2,779 |
8,023 |
0,00090 |
| 0,454 |
2,750 |
6,821 |
0,00129 |
| 0,459 |
2,765 |
5,732 |
0,00183 |
| 0,455 |
2,741 |
5,204 |
0,00224 |
| Taula 2: Relació entre força i distància
al focus en una paràbola |
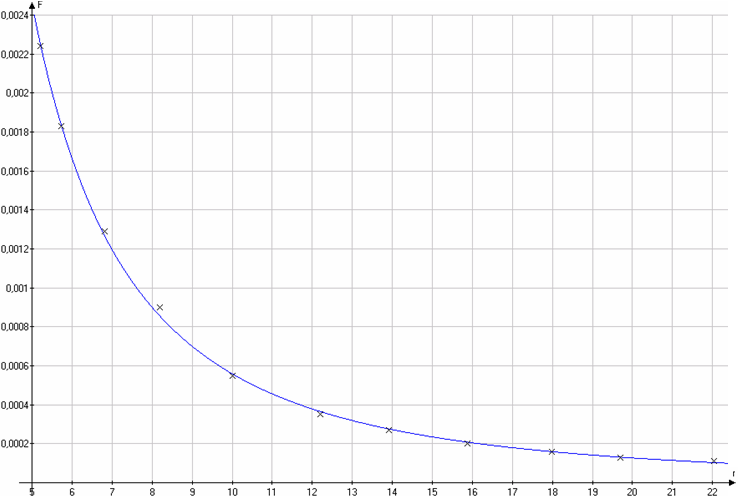 |
| Fig. 14: Llei de força versus distància obtinguda
amb una paràbola. |
Consideracions finals
Es pot proposar als alumnes fer diferents modificacions a l’experiència,
com per exemple canviar els paràmetres de l’el·lipse i estudiar
si això comporta modificar les conclusions finals.
Tanmateix es pot estudiar si en la mesura que més ens aproximem a la
condició 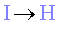 , millora
l’aproximació a una llei de proporcionalitat a l’invers del
quadrat de la distància. , millora
l’aproximació a una llei de proporcionalitat a l’invers del
quadrat de la distància.
Bibliografia
[1] Prentis, J, Bryan, F., Hesse, C., Mazzino, L. (2007). "Elliptical
Orbit ==> 1/ r2 Force". The physics teacher. Vol
45, pp 20-25.
[2] Goodstein, D., Goodstein, J. (1999). "La conferència perdida
de Feynman. El movimiento de los planetas alrededor del Sol". Tusquets
editores, Barcelona.
[3] Caamaño, A., Cortel A., Lozano, M.T., Pueyo L. (2004). "Física
2". Editorial Teide, Barcelona.
[4] Caturla, E. i Vidal, F. (1997). "Física 2". Editorial
Castellnou, Barcelona.
[5] Marti, J., Ruiz, E., Fraile, J.M. "Física i Química.
Crèdit comú 8". Grupo Santillana, Barcelona.
| Inici |
|
|
| ISSN:
1988-7930 Adreça a la xarxa:
www.RRFisica.cat Adreça electrònica:
redaccio@rrfisica.cat
difusio@rrfisica.cat
Comitè de redacció : Josep Ametlla, Octavi
Casellas, Xavier Jaén, Gemma Montanyà, Cristina Periago,
Octavi Plana, Jaume Pont i Ramon Sala.
Treballem conjuntament : Societat Catalana de Física,
Associació de Professores i Professors de Física i Química
de Catalunya,XTEC, Universitat Politècnica de Catalunya, Universitat
de Barcelona
|
   
Programació web: Xavier Jaén i Daniel Zaragoza.
Correcció lingüística: Serveis Linguïstics
de la Universitat Politècnica de Catalunya. |
Aquesta
obra està subjecta a una
Llicència
de Creative Commons

|
|
Recursos
de Física col·labora amb la
baldufa i també amb ciències
Revista del Professorat de Ciències de Primària i Secundària
(Edita: CRECIM-UAB)
|
|
|

 7/9
7/9 
 7/9
7/9 




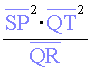

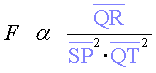

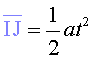
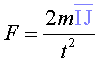
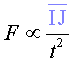
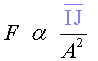
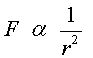 , n'hi ha prou
que es tracti d'una força central.
, n'hi ha prou
que es tracti d'una força central.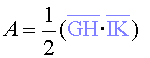
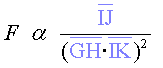

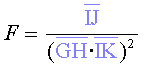 ( en
unitats
( en
unitats 
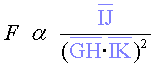 per trobar la llei de la força a la qual està sotmès un
cos que es mou segons aquest tipus de trajectòries.
per trobar la llei de la força a la qual està sotmès un
cos que es mou segons aquest tipus de trajectòries.