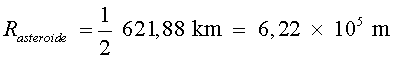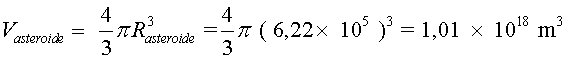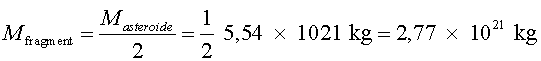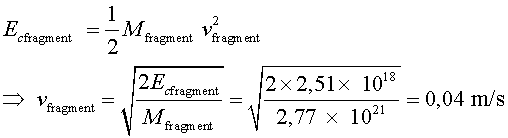Guia per al professorat
Introducció
Objectiu
Determinar si un asteroide de la mida de Texas es podria dividir
amb una bomba nuclear de manera que les dues meitats passessin per cada costat
de la Terra sense causar-hi danys, tal com es representa a la pel•lícula
Armageddon.
Nivell
1r de batxillerat. Es treballa cinemàtica en dues dimensions,
energia cinètica,...
Orientacions
S'introdueix el problema a partir del tràiler de la
pel·lícula : http://vimeo.com/59861066
. El problema es pot plantejar de dues maneres diferents:
Proposta no guiada
L’alumne (es pot treballar de forma individual o en
grup) ha de resoldre el problema sense cap altra informació que la que
surt a la pel•lícula. Ha de buscar les dades i fórmules
corresponents, plantejar les hipòtesis de treball (caldrà prendre
les hipòtesis més generoses possible per calcular la velocitat
de separació i la distància a què s’ha d’esquivar
l’asteroide). Es pot fer a l'aula (caldrà dues sessions) o com
a treball a casa.
Proposta guiada
L'alumne ha d’anar seguint el full de l'alumnat per
resoldre el problema. Es pot fer a l'aula (en aquest cas, una sessió
serà suficient) o com a treball a casa i, igual que abans, es pot fer
de forma individual o en grup.

 
Full de l'alumnat
Informació
Mira el video : http://vimeo.com/59861066
Les dues taules següents contenen les hipòtesis
i paràmetres necessaris per avaluar si la Terra podria ser salvada
pels herois d'Armageddon. Per tal d'esquivar
la Terra, suposem dues condicions:
1) La bomba nuclear ha de dividir en dos l'asteroide;
suposant que això passa, tota l'energia de la bomba es transforma
en energia cinètica.
2) La velocitat de separació de cada meitat
de l'asteroide ha de ser prou alta per poder-les separar el diàmetre
de la Terra i 800
milles més (tal com es diu a la pel•lícula)
en el temps que triguen a arribar a la Terra després de l'explosió.
S’han de considerar les hipòtesis més generoses
possible per calcular la velocitat de separació i la distància
a què s’ha d’esquivar l’asteroide. Òbviament,
si els càlculs indiquen que la Terra està condemnada al
fracàs, no hi ha cap raó per fer una anàlisi més
realista.
|
 |
| Fig. 2 |
|
| Hipòtesi |
Mida |
Observacions |
| Diàmetre de l'asteroide |
|
Distància més llarga entre
est i oest de Texas |
| Densitat de l'asteroide |
|
Densitat de la Terra |
| Forma de l'asteroide |
Esfera |
A la pel•lícula l'asteroide
és allargat, però per simplificar els càlculs
podem suposar que té una forma esfèrica |
| Rendiment de la bomba nuclear
|
|
Bomba nuclear “normal” 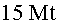 |
| Percentatge d'energia termonuclear convertida
en energia cinètica de les peces de l'asteroide |
|
Aquesta energia estarà repartida
a parts iguals en les dues meitats de l'asteroide i les separarà
de la manera més favorable. Òbviament, aquesta és
una hipòtesi molt generosa, ja que una gran part de l'energia
es transformarà en calor |
|
| Taula 1: Hipòtesis que s’han d’utilitzar
en l'anàlisi de la situació |
| Paràmetre |
Mida |
Observacions |
Velocitat de l'asteroide (cap a la Terra)
|
|
22500
mph en la versió original de la pel·lícula |
Temps que triga cada part de l'asteroide
a arribar a la Terra des de la detonació de la bomba |
|
És el temps que determina la barrera 0, temps límit
per fer explotar la bomba
|
Radi de la Terra |
|
|
Factor de conversió de milles en kilòmetres
|
|
|
Factor de conversió de megatones de
TNT a joules |
|
|
|
| Taula 2: Paràmetres que s’han d’utilitzar
en l'anàlisi de la situació |
Bibliografia
Sergio L. Palacios, La guerra de dos mundos, Ediciones
Robinbook Manontroppo

 
Solució
Es vol determinar si l'asteroide que es dirigeix
cap a la Terra, amb una velocitat determinada, podrà ser desviat
de la seva trajectòria en fer explotar una bomba nuclear que
trenqui en dos fragments l'asteroide.
Es tracta d'un problema de transferència d'energia, de cinemàtica,
però també de quantitat de moviment, de xocs...
Cal fer alguna suposició per poder resoldre el problema de manera
senzilla.
Esquema de la resolució
1. L'asteroide es mou a una certa
velocitat cap a la Terra. |
 |
| Fig. 4 |
|
2. En fer explotar la bomba, l'asteroide es trenca
en dues parts iguals. Tota l'energia de l'explosió es transforma
en energia cinètica i els dos fragments adquireixen una certa
velocitat, que caldrà calcular. Aquesta velocitat és perpendicular
al moviment inicial de l'asteroide (suposarem sempre la situació
més favorable)
Tindrem dues components de velocitat, la velocitat
inicial de l'asteroide 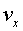 i
la velocitat deguda a l'explosió i
la velocitat deguda a l'explosió 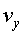 . La suma vectorial d'aquestes dues velocitats és la que proporcionarà
la velocitat total i la trajectòria de l'asteròide.
. La suma vectorial d'aquestes dues velocitats és la que proporcionarà
la velocitat total i la trajectòria de l'asteròide. |
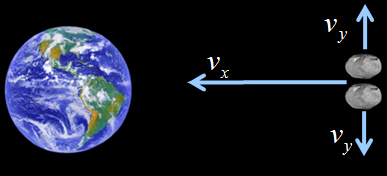 |
| Fig. 5 |
|
Càlculs
1. Energia transferida als fragments
de l'asteroide després de l'explosió.
Bomba: 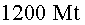 , ,
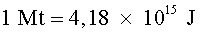
Energia proporcionada per la bomba: 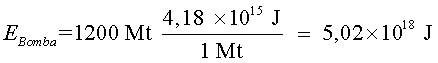
Suposarem que tota aquesta energia es transforma en energia
cinètica i que l'asteroide es fragmenta en dues parts iguals; cada part
rebrà la meitat d'aquesta energia cinètica:
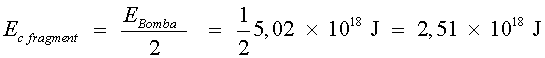
2. Amb l'energia cinètica es pot calcular la velocitat
que li proporciona la bomba a cada fragment, però ens caldrà trobar
la massa de cadascun dels fragments..
Radi de l'asteroide,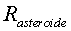
El diàmetre és 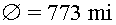 ,
és a dir ,
és a dir 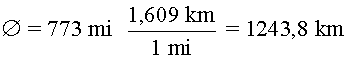 .
Així, el radi és .
Així, el radi és 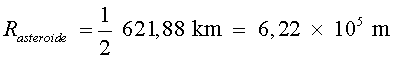
Volum de l'asteroide
La densitat de l'asteroide és 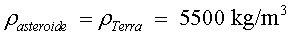
Forma: esfèrica (per simplificar els càlculs)
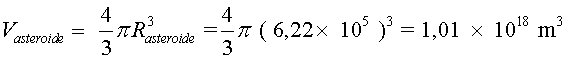
Massa de l'asteroide

Si es fragmenta en dues parts iguals:
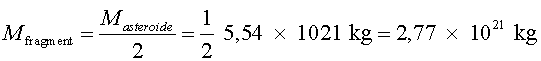
3. Ara podem calcular la velocitat
dels fragments:
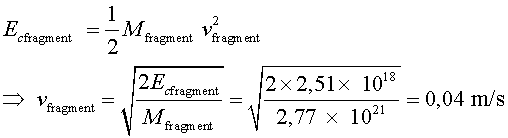
Cada fragment adquireix una velocitat en sentit perpendicular al moviment inicial
de l'asteroide de 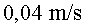 .
Força lent, oi? Serà suficient per evitar la col•lisió
amb la Terra? .
Força lent, oi? Serà suficient per evitar la col•lisió
amb la Terra?
4. Cal determinar la distància
que recorre l'asteroide en sentit perpendicular al moviment cap a la Terra a
partir de la component de la velocitat proporcionada per la bomba.
Com que volem comprovar la viabilitat del projecte, suposarem
que no hi ha atracció gravitatòria, ni entre els fragments ni
amb la Terra. Si, amb aquesta hipòtesi, el càlcul dóna
un resultat favorable al projecte, haurem de considerar aquest efecte; en cas
contrari, quedarà demostrat que no és viable. D’altra banda,
en no haver fricció a l'espai, suposarem una velocitat constant. Les
dues suposicions ens porten a considerar, per als fragments, un moviment rectilini
i uniforme 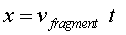
Segons la pel·lícula, la barrera zero es troba a 4 hores de la
col·lisió amb la Terra: 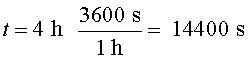
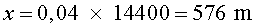
Distància recorreguda: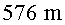
Si el radi de la Terra és  ,
és evident que aquests ,
és evident que aquests 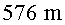 són molt poqueta cosa per evitar el desastre!
són molt poqueta cosa per evitar el desastre!
Quina decepció!

|

 7/9
7/9 









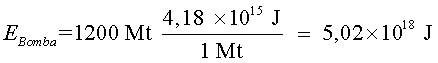
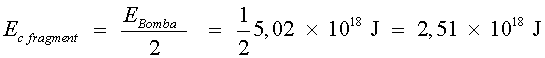
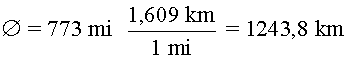 .
Així, el radi és
.
Així, el radi és