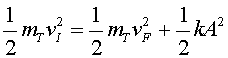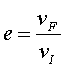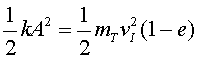On és l'energia dissipada?
Introducció
No fa gaire es va penjar a Youtube una experiència en
què es veia una bola que baixava per un pla inclinat. La baixada es realitzava
d'una manera un mica peculiar. Semblava que desafiava les lleis de la física
o, si més no, les lleis de la conservació. A l'adreça
http://www.youtube.com/watch?annotation_id=annotation_678608&feature=iv&src_vid=smuCwUKyhkg&v=7yZwj111f_4
podeu veure com baixa la bola i com es construeix.
En aquest racó volem aproximar-nos a donar una explicació
de com s'ho fa la bola per baixar de la manera com ho fa i, a la vegada, no
desafiar les lleis de la física, ni tan sols les de conservació.
El que no podem és donar una explicació detallada de com s’ho
fa concretament aquesta bola. Ens complicaríem la vida i no aniríem
al moll de l'os. Preferim ser més simples i analitzar alguns altres exemples
de sistemes que sembla que dissipen energia com a mecanisme essencial que n’explica
el comportament.
Molt cops, quan no sabem on ha anat a parar l'energia diem que s'ha dissipat
en forma de calor. En la majoria de casos no és del tot cert. No és
senzill saber quan es dissiparà o no l’energia "en forma de
calor". Si diem "l'energia s'ha dissipat", s'entendrà
que una part de l'energia mecànica, de la forma que sigui, ha desaparegut
i, com prediu la termodinàmica, contribuirà a l'augment de la
temperatura del mateix cos o d'algun altre cos que hi està en contacte.
En molts casos en què l'energia sembla que no es conserva, més
val que admetem que és perquè s'ha transformat en algun tipus
d'energia que no hem tingut en compte en els nostres càlculs i no perquè
hi hagi dissipació en el sentit que es dóna més amunt.
Per il•lustrar el que estem dient, tractarem alguns exemples conservatius
que sembla que dissipen energia. Són exemples de sistemes mecànics
senzills en què es donen transformacions d'energia mecànica de
diferents tipus: energia de translació, rotació i, finalment,
vibració.
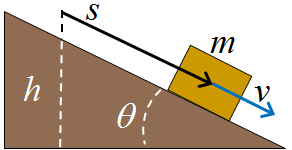
Translació: bloc que baixa per un pla inclinat sense
fricció
És el paradigma que es posa per a la conservació de l'energia
(vegeu la figura 1). Si no hi ha fricció, l'energia es conserva
i podem plantejar
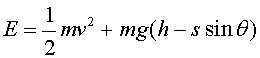 , ,
|
(1) |
on  és
el desplaçament del bloc en la direcció del pla comptat
a partir d'una referència. La velocitat a la qual va el bloc en
funció de és
el desplaçament del bloc en la direcció del pla comptat
a partir d'una referència. La velocitat a la qual va el bloc en
funció de  ,
la podem trobar sabent que l'energia (1) es conserva: ,
la podem trobar sabent que l'energia (1) es conserva:
|
 |
| Fig. 1 |
|
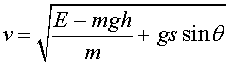
|
(2) |
Aquesta velocitat explica perfectament el comportament del bloc. Podem trobar-ne
fàcilment l'accelereració derivant l'energia (1):
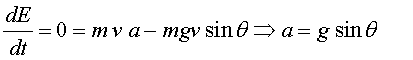
|
(3) |
L'acceleració és constant. Si el pla s'inclina molt, fins a arribar
a la vertical obtenim 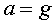 , com podem esperar.
, com podem esperar.
Translació i rotació: una esfera que rodola
per un pla inclinat
Ara l'esfera rodola. Aquesta és una forma de
moure's prou interessant i molt comuna. Resulta que l'esfera interacciona
amb el terra del pla no només amb la normal sinó també
amb la força de fricció. Tot i això, la força
de fricció no treballa mai. La força de fricció sobre
l'esfera està aplicada en cada instant al punt de contacte amb
el pla. Com que aquest punt no llisca, el desplaçament en el moment
de tocar el terra és nul. Cada cop que un punt de l'esfera toca
el terra té, en aquell mateix moment, una velocitat nul•la.
De resultes, encara que, necessàriament, hi sigui present la força
de fricció, el sistema és conservatiu. És a dir,
"no dissipa energia en forma de... calor!" . Si fem l'experiència,
veurem que els resultats obtinguts amb el bloc no ens serveixen. Si no
vigilem, haurem de dir que l'energia s'ha dissipat. Sí que podem
dir que l'energia potencial gravitatòria no es converteix enterament
en energia cinètica de translació.
Un tractament complet del problema és tenir en compte l'energia
cinètica de rotació.
La condició de rodolar l'escrivim 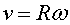 , on
, on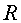 és
el radi de l'esfera. L'energia tindrà també el terme d'energia
cinètica de rotació. L'esfera no cal que sigui homogènia,
però sí que demanarem que tingui simetria esfèrica,
de manera que el centre de masses sigui al centre de l'esfera. és
el radi de l'esfera. L'energia tindrà també el terme d'energia
cinètica de rotació. L'esfera no cal que sigui homogènia,
però sí que demanarem que tingui simetria esfèrica,
de manera que el centre de masses sigui al centre de l'esfera.
|
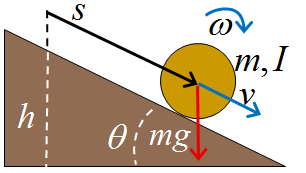 |
| Fig. 2 |
|
Escriurem el moment d'inèrcia de la manera següent: 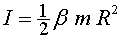 ,
on ,
on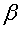 és un nombre
que depèn de la distribució interna de la massa. L'energia és
ara: és un nombre
que depèn de la distribució interna de la massa. L'energia és
ara:
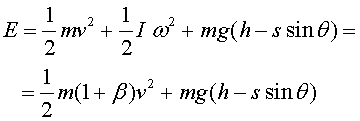
|
(4) |
La velocitat serà
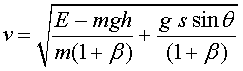
|
(5) |
I l'acceleració :
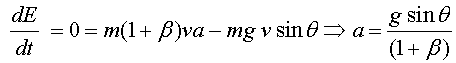
|
(6) |
L'acceleració és constant. Si el pla s'inclina molt, fins a arribar
a la vertical, i l'esfera sempre rodola, no obtenim 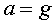 . Aquest cas, amb un valor gran de
. Aquest cas, amb un valor gran de 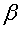 ,
és el que exlica el comportament de la roda de Maxwell. ,
és el que exlica el comportament de la roda de Maxwell.
Translació i rotació: una esfera inhomogènia
que rodola per un pla inclinat
Per simplificar, tractarem una closca esfèrica
de radi 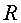 , sense
massa, que té fixada, a la meitat d'un radi, una massa puntual , sense
massa, que té fixada, a la meitat d'un radi, una massa puntual
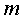 . Ara, la condició
de rodolar l'explicitarem una mica, més escrivint la relació
que hi ha entre l'espai recorregut i l'angle girat respecte de la normal, . Ara, la condició
de rodolar l'explicitarem una mica, més escrivint la relació
que hi ha entre l'espai recorregut i l'angle girat respecte de la normal,
 . Derivant, tindrem . Derivant, tindrem
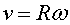 , on, compte, , on, compte,
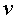 és la
velocitat del centre de l'esfera, que és la que percebem més
fàcilment com a observadors. és la
velocitat del centre de l'esfera, que és la que percebem més
fàcilment com a observadors.
El vector posició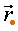 i la velocitat
i la velocitat de la massa són
de la massa són
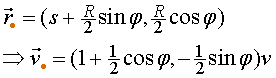
|
(7) |
L'energia serà
|
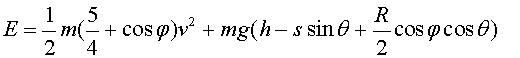
|
(8) |
La velocitat és ara
| 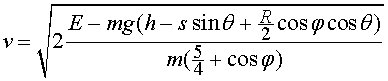
|
(9) |
|
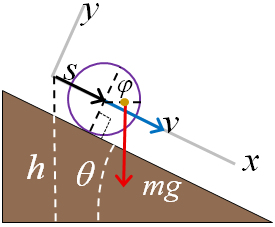 |
| Fig. 3 |
 |
Fig. 4: Variació de la velocitat per a un pla inclinat amb
un pendent de  . . |
|
Aquesta velocitat ja no és la d'un moviment uniformement
accelerat. És una velocitat que, tot i que de mitjana augmenta, no ho
fa de manera uniforme (vegeu la figura 4), però sí conservativa.
Translació : xoc elàstic d’una bola rígida
amb un terra dur i llis
A la figura 5 tenim un esquema del xoc d'una bola amb
un terra. Inicialment, la bola pot tenir un moviment de rotació.
Si el terra és llis, al final tindrà exactament la mateixa
rotació, de manera que la rotació de la bola serà
irrellevant. Que el terra sigui llis també vol dir que es conserva
la quantitat de moviment horitzontal:
| 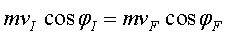
|
(10) |
Quant a l'energia, com que la bola és completament rígida
i el xoc és llis, només s'intercanvia l'energia cinètica
de translació:
| 
|
(11) |
Combinant (10) i (11) obtenim
|
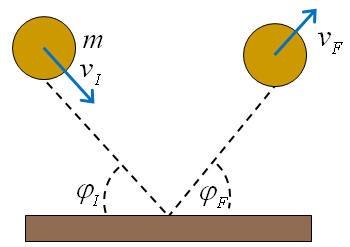 |
| Fig. 5 |
|
| 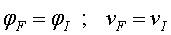
|
(12) |
(12) és conseqüència, entre altres coses, de la conservació
de l'energia. Pot no complir-se (12) i conservar-se l'energia? Vegem-ne algun
exemple.
Translació i rotació: xoc elàstic d’una bola rígida
amb un terra dur i aspre
A la figura 6 tenim el mateix tipus de xoc que a l’apartat
anterior, però ara considerem que la fricció amb el terra
és suficient perquè en cap moment llisqui. És a dir,
es tracta també d'un xoc conservatiu, si tenim en compte també
l'energia de rotació en el balanç energètic.
La condició que "durant" l'impacte la bola no llisca
es pot escriure com una condició de rodolament de la component
horitzontal de la velocitat final i la velocitat angular final:
| 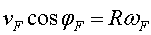
|
(13) |
La conservació de l'energia serà
| 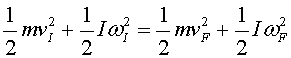
|
(14) |
|
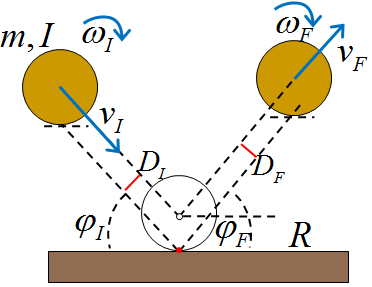 |
| Fig. 6 |
|
Si volem solucionar el problema, és a dir, trobar els
valors finals coneixent-ne els inicials, ens manca una equació. Cal afegir-hi
la conservació del moment angular respecte del punt d'impacte (vegeu
la figura 6). Per a això, cal tenir en compte que el paràmetre
d'impacte, que ens facilita el càlcul del moment angular de translació,
és (vegeu
la figura 6). Per a això, cal tenir en compte que el paràmetre
d'impacte, que ens facilita el càlcul del moment angular de translació,
és 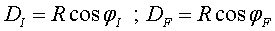 . Obtenim
així l'expressió de la conservació del moment angular: . Obtenim
així l'expressió de la conservació del moment angular:
| 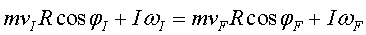
|
(15) |
Si, per no arrossegar massa paràmetres, ens restringim
a boles buides ( podem pensar en tennis o ping-pong conservatius), 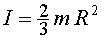 ,
obtenim ,
obtenim
| 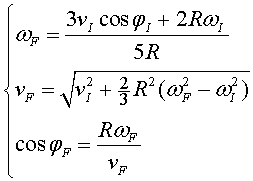
|
(16) |
La velocitat final pot ser més gran o més petita
que la inicial. Un cas particular interessant és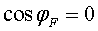 que
correspon al que podem anomenar, en una barreja d'argot físic i tennistic,
una deixada conservativa, que
correspon al que podem anomenar, en una barreja d'argot físic i tennistic,
una deixada conservativa,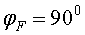 .
En aquest cas .
En aquest cas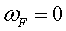 . Per
aconseguir aquest efecte, inicialment haurem de fer girar la bola a una velocitat
angular . Per
aconseguir aquest efecte, inicialment haurem de fer girar la bola a una velocitat
angular
| 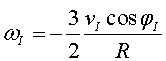
|
(17) |
és a dir , el que s'anomena un liftat (el
signe "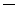 "
ens indica que la rotació és en sentit antihorari; vegeu la figura
6). La velocitat final serà, en aquest cas, "
ens indica que la rotació és en sentit antihorari; vegeu la figura
6). La velocitat final serà, en aquest cas,
| 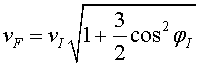
|
(18) |
més gran que la inicial. Les energies de translació i rotació
inicial han anat a parar a energia de translació final. Caldrà
que el tennista o el jugador de ping-pong valori si aquesta deixada li
surt o no a compte.
Translació i vibració: xoc elàstic d’un cos
no rígid amb un terra dur
A la figura 7 tenim una pilota elàstica que, deixada
anar verticalment, xoca (bota) amb el terra i no aconsegueix l'alçada
inicial. En aquest cas, no hi ha rotació inicial ni és possible
un intercanvi d'energia de translació amb una de rotació.
El xoc és completament elàstic, però sembla que hi
hagi dissipació. En aquest cas, una part de l'energia de translació
s'ha transformat en energia de vibració, que, al cap d'una estona,
sí que es dissipa, però no com a conseqüència
del xoc.
|
 |
| Fig. 7 |
|
 |
| Fig. 8 |
|
Per mirar d'explicar el que passa, fem un model de
cos no rígid com el de la figura 8. En lloc d'una pilota tenim
dues masses iguals enganxades amb una molla sense massa. Durant el procés
de xoc prescindirem de la gravetat. De fet, podem prescindir de la gravetat
i pensar que llencem el cos contra el terra a una certa velocitat de translació
sense que hi hagi vibració. El que volem analitzar és com
canvia aquesta velocitat com a conseqüència del xoc.
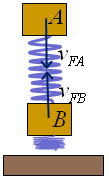
A la figura 9 tenim el cos just abans de xocar amb el
terra. El punt vermell és el centre de masses i, si el cos no vibra,
la velocitat d'aquest és la de qualsevol altra part del cos. Els
dos blocs van a la mateixa velocitat, com es veu a la figura 10.
|
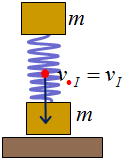 |
| Fig. 9 |
|
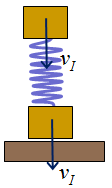 |
| Fig. 10 |
|
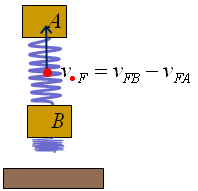
A la figura 11 el cos ja ha xocat amb el terra. En
tractar-se d'un xoc elàstic i dur, la velocitat després
del xoc és, pel que fa al mòdul, la mateixa que abans del
xoc, però de sentit contrari. A continuació, la molla es
comprimeix i les velocitats disminueixen, però sempre amb el mateix
mòdul. En arribar al final de la compressió, suposant que
la molla és prou dura perquè els dos blocs no es toquin,
començarà l’expansió de la molla fins que,
quan els dos blocs arribin a tenir el mateix mòdul de velocitat
que tenien en iniciar la compressió, el bloc inferior torna a xocar
amb el terra (vegeu la figura 12).
|
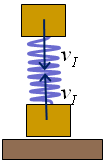 |
| Fig. 11 |
|
 |
| Fig. 12 |
|
A la figura 13 veiem com el bloc inferior xoca per
segona vegada amb el terra i adquireix una velocitat igual que el bloc
superior, amb la mateixa direcció i el mateix sentit. Així,
finalment, el conjunt del cos surt amb una velocitat igual a la velocitat
a què ha arribat. Compareu la figura 9 i la 14. El procés
ha requerit un parell de xocs i s’hi ha hagut d’esmerçar
un cert temps, però el resultat és el mateix que si el cos
fos totalment rígid. No s'ha produït cap intercanvi d'energia
entre l’energia de translació i la de vibració.
Abans de veure com ha de ser un xoc per tal que s'intercanviï energia
de translació a energia de vibració, podem utilitzar el
model tal com el tenim ara per fer una experiència que no és
de xoc però que aconsegueix l'efecte que ens interessa.
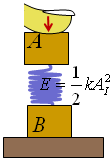
A la figura 15 veiem el nostre model, en repòs i pressionat contra
el terra de manera que la molla queda comprimida i acumula una certa energia
inicial 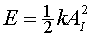 . En
aquest moment, el deixem anar. La molla es va descomprimint. El bloc . En
aquest moment, el deixem anar. La molla es va descomprimint. El bloc  guanya
velocitat i el guanya
velocitat i el  resta
quiet, per causa que rep una força externa, la normal del terra,
que impedeix que es mogui avall. Notem que aquesta força no treballa,
no dissipa energia. Just quan acaba la descompressió de la molla,
la situació és la de la figura 16. resta
quiet, per causa que rep una força externa, la normal del terra,
que impedeix que es mogui avall. Notem que aquesta força no treballa,
no dissipa energia. Just quan acaba la descompressió de la molla,
la situació és la de la figura 16.
|
 |
| Fig. 13 |
|
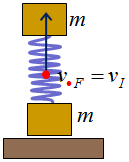 |
| Fig. 14 |
|
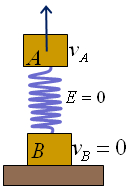
Tota l'energia de la molla se l'emporta el cos en forma d'energia cinètica:
en forma d'energia cinètica: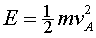 .
Això no vol dir que el conjunt, el centre de masses, vagi a aquesta
velocitat. Podem calcular en aquest instant la quantitat de moviment total
i la velocitat del centre de masses. Recordem que el bloc .
Això no vol dir que el conjunt, el centre de masses, vagi a aquesta
velocitat. Podem calcular en aquest instant la quantitat de moviment total
i la velocitat del centre de masses. Recordem que el bloc 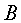 encara està aturat. Com a conseqüència aquesta velocitat
serà
encara està aturat. Com a conseqüència aquesta velocitat
serà 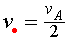 .
Com que ara el conjunt del cos ja no rep cap força externa (recordem
que, per simplificar, hem eliminat la gravetat), el cos continuarà
amb aquesta velocitat constant (figura 17). .
Com que ara el conjunt del cos ja no rep cap força externa (recordem
que, per simplificar, hem eliminat la gravetat), el cos continuarà
amb aquesta velocitat constant (figura 17).
Ara, de l'anàlisi energètica tenim: l'energia
de translació que té el cos (el conjunt i i ) és
) és 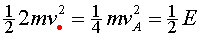 ,
que només és la meitat de l'energia inicial de la molla
en comprimir-la. Així doncs, el cos també vibrarà,
amb una amplitud més petita en comparació amb la inicial,
concretament ,
que només és la meitat de l'energia inicial de la molla
en comprimir-la. Així doncs, el cos també vibrarà,
amb una amplitud més petita en comparació amb la inicial,
concretament  . .
|
 |
| Fig. 15 |
|
|
|
| Fig. 16 |
|
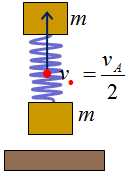 |
| Fig. 17 |
|
Tornem ara als xocs. Mirem de trobar la manera d'intercanviar
energia de translació i vibració mitjançant un xoc.
A la figura 18 veiem el model de cos no rígid anterior però
lleugerament complicat amb l'afegitó d'una segona molla que farà
que l'impacte amb el terra no sigui instantani. Com abans, el bloc inferior
arriba al terra amb la velocitat 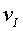 ,
la mateixa que té el bloc superior (figura 19). Sempre suposarem
que les molles són de tal manera que estan dins el seu límit
elàstic. ,
la mateixa que té el bloc superior (figura 19). Sempre suposarem
que les molles són de tal manera que estan dins el seu límit
elàstic.
|
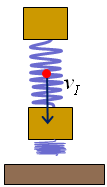 |
| Fig. 18 |
|
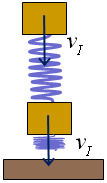 |
| Fig. 19 |
|
on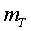 és la massa total,
és la massa total, 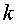 la
constant de la molla que uneix els dos blocs i la
constant de la molla que uneix els dos blocs i  l'amplitud de les oscil·lacions.
l'amplitud de les oscil·lacions.
El repartiment de l'energia inicial entre la final de translació
i la de vibració depèn, com veiem, de les característiques
del cos, la duresa de les molles i les masses. Nosaltres hem tractat només
un model que ens ajuda a entendre què passa en la realitat. Els objectes
reals són en general molt més complexos. El que es fa habitualment
és definir un coeficient de restitució 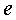 mesurable experimentalment:
mesurable experimentalment:
| 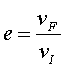
|
(20) |
Així, podem dir que un xoc es dóna amb un coeficient de restitució
de tal valor. Ara, com hem vist, això no vol dir que no se’n conservi
l'energia. L'energia de vibració es pot escriure, si coneixem el coeficient
de restitució, com
| 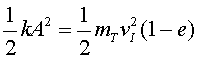
|
(21) |
Conclusió
Tornant a la bola de Youtube, podem dir que no necessàriament
es tracta d'un comportament no conservatiu. Al revés, és concebible
aquest comportament com a conseqüència de la conservació
de l'energia. La presència d'un fluid viscós no significa necessàriament
que no es conservi l'energia. Els moviments interns d'aquest fluid poden ser
semblants a un rodolament (llefiscós, certament) en què la dissipació
de l'energia no té per què ser el més important. La velocitat
de la bola de Youtube té un comportament que no és tan allunyat
del que es mostra a la gràfica de la figura 4.

|

 9/9
9/9 


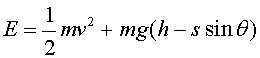 ,
,
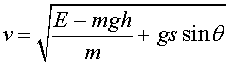
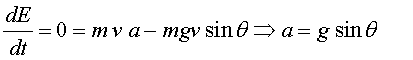

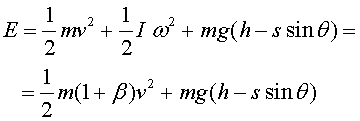
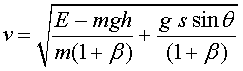
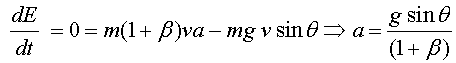
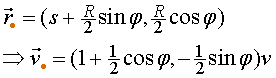
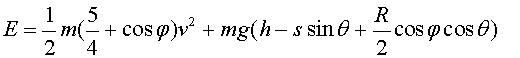
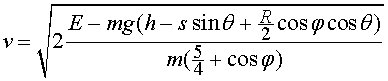




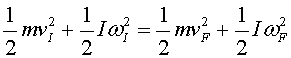

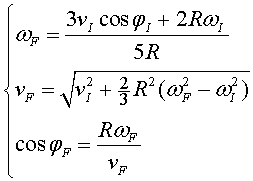
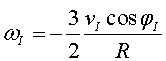
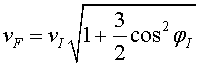








 .
.