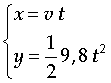Introducció

L’accelerador de Gauss és un dispositiu format per una colla d’imants i boles metàl•liques col•locades en un carril. És un sistema de diverses etapes, de manera que, a partir d’una configuració geomètrica determinada, permet anar accelerant la bola, que va col•lidint amb els diferents imants. Aquest experiment permet treballar els conceptes de treball i energia potencial, transformació de l’energia (potencial magnètica) en energia cinètica, conservació de la quantitat de moviment i també l’abast màxim en el tir parabòlic. Aquest dispositiu va ser ideat i patentat l'any 1904 pel físic noruec Kristian Birkeland.
En aquest treball hem construït un accelerador de quatre etapes (imants) i hem mirat de relacionar el nombre d’etapes que hi afegim successivament amb la velocitat de sortida de la darrera bola que ens dóna l’energia cinètica del sistema. La velocitat de sortida l’hem calculat amb un dels mètodes que es proposa en la bibliografia, que consisteix en relacionar l’abast amb l’altura del carril respecte al terra. També hem investigat una mica i proposem una disposició geomètrica i un concepte diferent que permeten assolir acceleracions molt més grans amb el mateix nombre d’etapes que en l’accelerador de Gauss. A aquesta nova disposició l'anomenem accelerador revolucionat. Per fer aquest terball hem disposat de l’ajuda de dues publicacions molt interessants que es troben lliures a Internet. Vegeu [1,2].

Fig. 1

Construcció de l’accelerador de Gauss

Podem construir molt fàcilment un accelerador de Gauss. A continuació exposem els passos a seguir.

Material

Procediment

A la figura 1 podem veure els dos tubs de PVC encolats que fan de carril d’acceleració. Aquest tipus de carril és molt fàcil de fabricar i permet treballar amb boles de diferents mides. A la figura 2 podem veure un accelerador carregat de quatre etapes. Si volem treure conclusions fiables dels diferents abasts màxims que assoleix la darrera bola, és convenient fixar el carril amb cinta aïllant a una taula o un suport per fer els llançaments,

Com funciona l’accelerador de Gauss

Fig. 3 Accelerador carregat. La bola vermella és un imant i la blava una bola d’acer.

Fig. 4 Accelerador descarregat. La bola vermella és un imant i la blava una bola d’acer.

L’accelerador de Gauss és un dispositiu que transforma l’energia potencial magnètica en energia cinètica. En una primera etapa l’accelerador disposa d'una una bola-imant seguida de dues boles-acer. Aquest conjunt de tres boles, després de la primera col•lisió, es transforma en un conjunt bola-acer, bola-imant, bola-acer. Vegeu les figures 3 i 4. Cal tenir en compte tres punts molt importants que ens indiquen en la bibliografia:

1) Els imants han de tenir la mateixa alineació nord-sud en la direcció del carril. Han d’estar separats una distància d’uns 9 cm. Pot passar que aquesta distància s’hagi d’ajustar una mica en cada cas.

2) Els imants han d’estar ben fixats amb cinta aïllant, però han de permetre una mica de retrocés per tal de conservar la quantitat de moviment. Si els fixem molt rígidament, l’accelerador no funciona.

3) Per disparar l’accelerador acostem una bola-acer suaument al primer imant del carril, que serà el que provoqui la reacció en cadena. S’ha comprovat estadísticament [1] que quan augmenta la velocitat d’aproximació de la primera bola disminueix la velocitat de sortida de l'última. Experimentalment també és fàcil de comprovar-ho amb un parell de llançaments.

Per quina raó física funciona l’accelerador?

L’accelerador és un dispositiu que acumula energia potencial magnètica. La disposició de les boles-imant i les boles-acer a l'inici (accelerador carregat) és una situació inestable (les dues boles-acer en fila enganxades) i no simètrica. Al final veiem que hi ha un equilibri i una simetria en la disposició de les boles-imant . En l’accelerador carregat hi ha 4 interaccions bola-imant/bola-acer a una distància entre centres igual a 2R (R és el radi de la bola) i quatre interaccions bola-imant/bola-acer a una distància 4R. Al final, en l’accelerador descarregat, hi ha 8 interaccions bola-imant/bola-acer a una distància 2R.
En un sistema de dues boles-acer i una bola-imant tenim dues situacions d’equilibri estable (vegeu la figura 6); és a dir que si movem o desplacem algun objecte del sistema de la seva posició inicial, el sistema torna a la mateixa posició.

Fig. 6: Equilibri estable.

En aquest sistema també hi ha dues posicions equivalents d’equilibri inestable que corresponen a les dues boles-acer alineades amb un pol de l’imant (vegeu la figura 7). Si pertorbem una mica aquest sistema no torna a la posició inicial, sinó que busca una de les posicions anteriors d’equilibri estable de la figura 6. Aquesta inestabilitat queda una mica contrarestada per la geometria del carril..

Fig. 7: Equilibri inestable

Podem calcula l’energia magnètica de cada etapa seguint les pautes que ens indiquen a la bibliografia.

Com funciona l’accelerador revolucionat?

Fig. 8 Accelerador carregat .La bola vermella és un imant i la blava una bola d’acer.

Fig. 9 Accelerador descarregat. La bola vermella és un imant i la blava una bola d’acer.

L’accelerador revolucionat funciona amb 8 boles-imant enlloc de les 4 boles-imant del de Gauss. També veiem que hi ha una pèrdua de simetria abans i després de disparar.

Per iniciar-lo acostem suaument una bola-imant al grup de la primera etapa i iniciem la reacció en cadena. Veiem com, contrariament al cas anterior, ara hi ha hagut una pèrdua de simetria, però en canvi hem guanyat diferència d'energia potencial magnètica pel fet que s’han produït 4 interaccions noves d’atracció bola-imant/bola-imant, que són molt estables i baixen molt l’energia potencial del sistema. Aquest fet es manifesta en l’augment espectacular de l’energia cinètica de la bola-acer que surt disparada.

En l’accelerador revolucionat és molt important que, a l'inici, quan carreguem l’accelerador, totes les boles-imant tinguin el mateix sentit de polaritat nord-sud, ja que, d’aquesta manera, quan una bola-imant es desplaça d’una etapa a la següent ja quedarà encarada i no li caldrà rodolar per aconseguir la situació de mínima energia potencial. La primera bola-imant que inicia el sistema, primer rodola suaument però quan s’apropa al primer imant llisca ràpidament. Les boles-imant que salten en les altres etapes només llisquen, la bola-acer que surt disparada al final pot rodolar a més de lliscar en desplaçar-se.
En l’accelerador revolucionat l’abast corresponent a una etapa (dues boles-imants) és gairebé el mateix que l’obtingut en el de Gauss en quatre etapes (quatre boles-imants).
En els vídeos [3] i [4] podem veure la l’energia que acumula l’accelerador de Gauss en dues etapes. La podem comparar amb l’energia de l’accelerador revolucionat també en dues etapes.

Quina experiència podem fer a l’aula amb l’accelerador?

A l’aula proposem fer primer l’accelerador de Gauss i anar relacionant el nombre d’etapes amb l’abast màxim. Per què l’experiència funcioni, cal fixar el tub llançador a una taula o suport horitzontal.
Cal mesurar l’altura des de la qual surt disparada la bola. Hem d’anar fixant les boles-imant a una distància de 9 cm i procurar que estiguin alineades en la mateixa direcció nord-sud.

Una de les activitats que podem fer a l’aula és variar aquesta distància entre boles-imant per optimitzar la nostra experiència. Hem de mesurar, en cada cas l'abast màxim . Si cal, fem dos cops el llançament i fem la mitjana.

Amb l’altura de sortida , 74 cm en el nostre cas, i l’abast màxim podem calcular la velocitat horitzontal de sortida de la bola i la seva energia cinètica final utilitzant les expressions de la teoria del tir parabòlic:

Amb la massa de la darrera bola (13,87 g) i la velocitat podem calcular l’energia mecànica del sistema que s’ha transformat finalment en energia cinètica , ignorant els fregaments i les rotacions de les boles. Després podem repetir l’experiència amb l’accelerador revolucionat; en aquest cas, les velocitats i l’acceleració són molt més elevades i ens podem trobar que es trenqui algun imant. És recomanable protegir-los amb una mica de cinta adhesiva. En algunes experiències descrites a la bibliografia posen la darrera bola una mica més petita per obtenir velocitats i abasts més grans; d’aquesta manera s’aconsegueixen amb l’accelerador de Gauss velocitats al voltant de 5,2 m/s.

Taula 1: Dades que hem obtingut: accelerador de Gauss

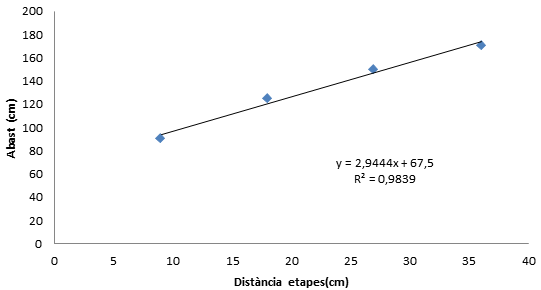
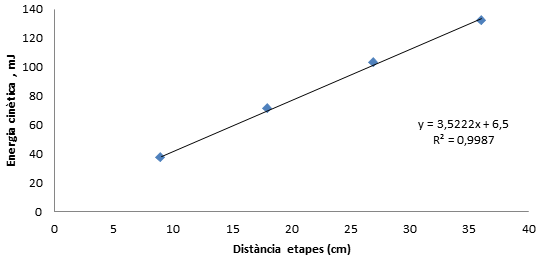
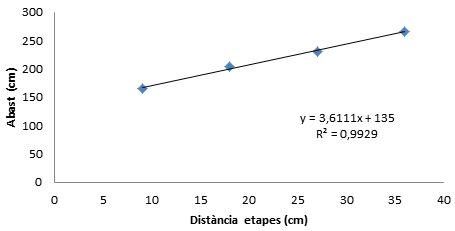
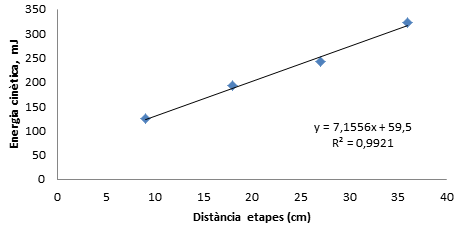
A continuació podem veure les gràfiques que relacionen les diferents etapes amb l’abast i amb l’energia cinètica del sistema.

Fig. 10: Gràfic abast/etapes

Fig. 11: Gràfic energia cinètica/etapes

Dades que hem obtingut amb l'accelerador revolucionat.

Taula 2:Dades que hem obtingut: accelerador revolucionat.

A continuació podem veure les gràfiques que relacionen les diferents etapes amb l’abast i amb l’energia cinètica del sistema.

Fig. 12: Gràfic abast/etapes

Fig. 13: Gràfic energia cinètica/etapes

Conclusions

Amb els dos tipus de disposicions dels imants veiem que en surten uns gràfics i uns coeficients de regressió bastant ben ajustats.
Si comparem els dos tipus de disposicions veiem que el revolucionat ens dóna pendents i ordenades en l'origen més grans, ja que cada etapa acumula més energia en relació amb la disposició del de Gauss.
Una pregunta que ens podem fer, i que segurament ens faran els nostres alumnes, és què passa si anem augmentant el nombre d’etapes. En aquest cas, s’arriba a una mena de saturació i és per la linealitat d’una manera semblant a com les molles perden elasticitat. Ho hem comprovat amb 8 etapes i es confirma el que diu la teoria.
També ens podem preguntar quina disposició és més eficient, és a dir, quina acumula més energia per nombre d’imants. Per contestar a aquesta pregunta hem fet la taula següent:

Taula 3: Comparació d'eficiència entre els dos acceleradors.

Observem que en ambdós casos els acceleradors perden eficiència a mesura que va augmentant el nombre d’etapes.
En les primeres etapes l’accelerador revolucionat és més eficient amb molta diferència, que va minvant quan ens apropem a la saturació del sistema. En tots els casos l’accelerador revolucionat és més eficient.

Bibliografia

ISSN: 1988-7930 DL:  B-31773-2012   Adreça a la xarxa: www.RRFisica.cat    Adreça electrònica: redaccio@rrfisica.cat  difusio@rrfisica.cat
Comitè de redacció : Josep Ametlla, Octavi Casellas, Xavier Jaén, Octavi Plana, Jaume Pont i Santi Vilchez
Treballem conjuntament : Societat Catalana de Física, Associació de Professores i Professors de Física i Química de Catalunya,XTEC, Universitat Politècnica de Catalunya, Universitat de Barcelona

Recursos de Física col·labora amb ciències Revista del Professorat de Ciències de Primària i Secundària (Edita: CRECIM-UAB)