núm 3 |
Primavera del 2009 |
Societat Catalana de Física |
| Inici |
| Sumari |   2/9 2/9  |
| Determinació del coeficient de fricció Lorenzo Martínez |
|
| En aquesta activitat es vol determinar el coeficient de fricció d'un canó fet en miniatura i carregat amb pólvora. El tret del canó es filma i se'n fa l'estudi amb un programa de tractament d'imatges de vídeo. Aplicant els teoremes de conservació de la mecànica i interpretant les gràfiques posició-temps i velocitat-temps podem calcular el coeficient de fricció del canó amb el terra. La proposta està pensada per realitzar-la amb l'alumnat de primer de batxillerat. |
IntroduccióEstem envoltats de fricció. Gràcies a la fricció podem escriure amb el bolígraf, el llapis, la ploma, també podem caminar tranquil•lament. Ja sabeu què passa si caminem damunt un llac o una superfície glaçada! Però, encara més:
Però, com podem trobar les forces degudes a la fricció i, per tant, com podem trobar el coeficient de fricció? Guia del professoratObjectius
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Què haurieu d'aprendre en aquesta activitat?
|
 |
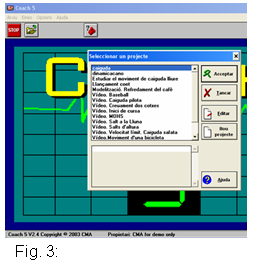
| A continuació, descrivim el procés que cal seguir utilitzant el Coach com a programari d'anàlisi de vídeo. Si utilitzeu un programa diferent, els processos segurament seran similars. 2) Inici del CoachObriu el CMA Coach 5 Studio MV Author, creeu un Nou projecte i, després, una Nova activitat, amb un Vídeo de dades (haureu d'afegir la pel·lícula del tret del canó). Us trobareu una pantalla com la de la figura 3. |
|
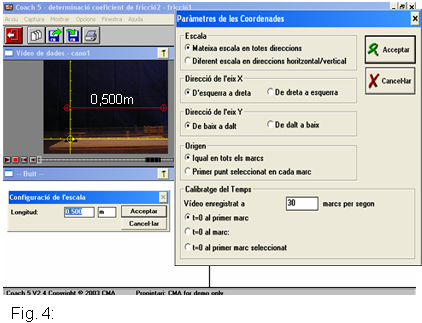
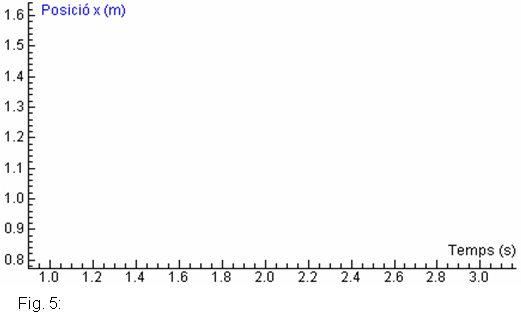
3) ConfiguracióA la finestra del vídeo (vegeu la figura 4), feu clic amb el botó dret del ratolí i configureu els paràmetres: introduïu el valor de l'escala, en metres, i moveu els extrems del regle fins a ajustar-los a la imatge, de manera que permeteu que el programa faci el calibratge. Podeu utilitzar la imatge del canó de la figura 4 per fer el calibratge. En aquesta es veu que la taula emprada en l'experiència té una longitud real de 0,500 m. 4) PrediccióQ1) |
 |
 |
5) Recull de dades
Continueu ara amb l'anàlisi del vídeo.
Cliqueu al botó verd ![]() Iniciar,
per començar les mesures. Amb la creu que apareix sobre
el vídeo, feu clic en el punt que voleu capturar. Repetiu la mateixa
acció fins que s'acabin els fotogrames del vídeo
Iniciar,
per començar les mesures. Amb la creu que apareix sobre
el vídeo, feu clic en el punt que voleu capturar. Repetiu la mateixa
acció fins que s'acabin els fotogrames del vídeo
6) Gràfica posició – temps
Inseriu les dades capturades en forma de gràfica posició-temps.
Cliqueu a la icona Mostrar gràfica, per crear una Nova
gràfica (poseu-hi el nom adient). En el rang de dades
C1, trieu la variable Temps, i en el rang de dades
C2, la variable P1-x. En cada variable podeu
configurar els eixos, el nom de la magnitud, les unitats, el nombre de decimals,
els valors mínims i màxims...).
Finalment, cliqueu al botó Acceptar i deseu la gràfica
(fent clic) en qualsevol de les tres finestres lliures.
7) Tipus de moviment
Aneu a la finestra de la gràfica posició-temps.
Feu clic a la icona del martell (botó d'eines)
i aneu a Crear/Editar gràfica. Canvieu els valors màxims
i mínims de les coordenades. Per al temps poseu-hi de 0
a 1s i per la posició
de 0 a 0,30
m
Feu clic de nou al botó d'eines i aneu a Processament/Filtrar
corba. Fixeu-vos que hi ha tres trams.
Q3)![]() I el de rectilini uniforme?
I el de rectilini uniforme?
Q4)![]() I el de moviment uniformement desaccelerat ?
I el de moviment uniformement desaccelerat ?
Q5)![]() Escriviu
les semblances i les diferències entre la gràfica de la vostra
predicció i la gràfica que heu obtingut.
Escriviu
les semblances i les diferències entre la gràfica de la vostra
predicció i la gràfica que heu obtingut.
8) Com varia la velocitat del canó?
Continueu en la mateixa finestra de posició - temps.
Feu clic a la icona del martell (botó d'eines)
i aneu Processament/Derivada. Després de prémer
el botó Iniciar, marqueu el botó Nova
gràfica per situar la gràfica en una finestra nova. Poseu-hi
després el nom "Velocitat - temps" (cliqueu a la icona del
martell/Crear/Editar nova gràfica i escriviu el nom
en el camp Nom:)
Q6)![]() Assenyaleu
els tres trams del moviment i completeu la taula següent:
Assenyaleu
els tres trams del moviment i completeu la taula següent:
Tipus de moviment |
Temps inicial (s) |
Temps final (s) |
Posició inicial (m) |
Posició final (s) |
Velocitat inicial (m/s) |
Velocitat final (m/s) |
Tram A MRUA a >0 |
||||||
Tram B MRU a = 0 V= constant |
||||||
Tram C MRUA a <0 |
9) Càlcul de la velocitat del perdigó
A partir d'aquí la notació que utilitzarem
serà la següent: lletres majúscules per al canó i
minúscules per al perdigó; els subíndexs 1
i 2 es referiran
als instants abans i després de l'explosió, respectivament;
el subíndex 3
correspondrà a l'instant final (el canó queda finalment aturat).
Durant l'explosió, podem aplicar la conservació de la quantitat
de moviment, ja que el temps de l'explosió és prou petit
perquè les forces de fricció es facin notar. Ho podeu comprovar
si mireu la gràfica x
= x(t): entre 0,1.
i 0,2 s. El sistema
que estudiem és el conjunt canó - perdigó i en aquesta
situació la quantitat de moviment es conserva:
0 = P1 + p1 = P2 + p2
A partir de la gràfica velocitat–temps, trobeu la velocitat de
retrocés del canó, mirant la pel·lícula fotograma
a fotograma, fins a arribar al fotograma 185. Anoteu-ne el valor. Si mireu la
pel·lícula fotograma a fotograma, el moviment està comprès
entre els fotogrames 180 i 189 i l'explosió acaba en el 185. En
aquest instant la velocitat assolida és màxima.
Q7)![]() Velocitat
canó, V2
=
Velocitat
canó, V2
=
Peseu el canó i anoteu la massa (en quilograms) del canó. Aquí
us donem el valor corresponent al canó utilitzat en el vídeo video_cano.mov.
Massa del canó, M
=28,6·10-3 kg.
Peseu 10 perdigons i trobeu la massa (en quilograms) d'un perdigó.
Aquí us donem el valor del perdigó utilitzat en el vídeo
video_cano.mov
Massa d'1 perdigó,
m =0,2·10-3
kg.
Aplicant la conservació de la quantitat de moviment 0
= M2 V2 + m2 v2, trobeu
la velocitat del perdigó
Q8)![]() Velocitat
del perdigó, v2
=
Velocitat
del perdigó, v2
=
Q9)![]() Per
què aquesta velocitat surt negativa? Quin significat té, en aquest
cas, el signe?
Per
què aquesta velocitat surt negativa? Quin significat té, en aquest
cas, el signe?
10) Càlcul del coeficient de fricció dinàmica i aplicació
del teorema treball - energia
Passat un temps molt petit, el canó, a causa de l'acció
de la fricció sobre les rodes, perd velocitat i s'aturar, desprès
de recórrer una distància d.
Quina és aquesta distància?
Q10)![]() Distància
fins aturar-se d
=
Distància
fins aturar-se d
=
Velocitat final del canó, V3
=0.
Velocitat inicial del canó = velocitat màxima V2
.
Podem calcular ara el coeficient de fricció tenint en compte que l'única
força que actua sobre el canó després de l'explosió
és la de fricció ![]() .
Si A és
l'acceleració del canó després de l'explosió, tenim
.
Si A és
l'acceleració del canó després de l'explosió, tenim
![]() i substituïm la
força de fricció pel seu valor màxim
i substituïm la
força de fricció pel seu valor màxim ![]() ,
obtenim
,
obtenim
(1) |
Sabem també que
(2) |
Si aïllem l'acceleració A de l'equació (2) i la substituïm en la (1), tenint en compte el valor nul de V3, obtenim
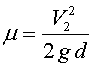 ,
,
Q11)![]() de
manera que el coeficient de fricció és
de
manera que el coeficient de fricció és ![]() .
.
Q12)![]() Què
vol dir que una magnitud (com ara el coeficient de fricció) és
adimensional?
Què
vol dir que una magnitud (com ara el coeficient de fricció) és
adimensional?
Ara, aplicant el teorema de les forces vives (treball-energia), trobeu el valor
del coeficient de fricció i compareu-lo amb el que heu trobat abans.
W = Ec3 - Ec2
en el nostre cas
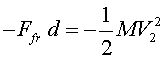
i substituint la força de fricció
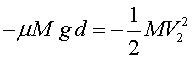
Q13)![]() Substituïu
les dades i trobeu el valor del coeficient de fricció.
Substituïu
les dades i trobeu el valor del coeficient de fricció.![]()
Q14)![]() Sabríeu dir quina és, en cada interval, l'equació
de la posició en funció del temps?
Sabríeu dir quina és, en cada interval, l'equació
de la posició en funció del temps?
Q15)![]() Resoleu en un full apart el problema següent, aplica-hi la conservació
de la quantitat de moviment:
Resoleu en un full apart el problema següent, aplica-hi la conservació
de la quantitat de moviment:
Un canó de 5000 kg dispara un projectil de 40 kg amb una velocitat horitzontal de 300 m/s des d'un penya-segat de 60 m sobre el nivell del mar. El canó està inicialment en repòs, sobre una plataforma que té un coeficient de fricció de 0,2 amb el terra (la fricció amb l'aire és negligible). Calculeu: a) la velocitat del canó en l'instant en que surt el projectil;b) l'espai que recorre el canó sobre la plataforma a causa del tret, i c) l'abast i la velocitat amb que el projectil arriba a l'aigua.
Solucions
Aquí podeu veure un resultat pràctic d’un grup de 1r de batxillerat del curs 2005-2006.
Dades
De la gràfica x = f (t) i v = f (t) obtenim les dades de la taula.
Tram |
Temps inicial (s) |
Temps final (s) |
Posició inicial (m) |
Posició final (s) |
Velocitat inicial (m/s) |
Velocitat final (m/s) |
Tram A MRUA a >0 |
0.00
|
0.27
|
0.00
|
0.07
|
0
|
0.77 |
Tram B MRU a = 0 V= constant |
0.27
|
0.33
|
0.07
|
0.13
|
0.77 |
0.76 |
Tram C MRUA a <0 |
0.33
|
0.53
|
0.13 |
0.21 |
0.76 |
0 |
Per trobar la velocitat del perdigó suposem que durant l’explosió (temps molt petit) es compleix la conservació de la quantitat de moviment.
M
massa canó,
M = 28,6 g = 28,6 / 1000 kg
m massa
perdigó, m
= 0,2 g = 0,2 / 1000 kg
A la figura 6 podem veure les taules i gràfiques que s'obtenen amb el Coach.
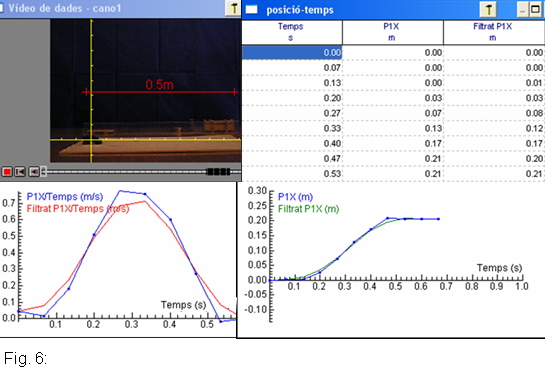 |
Agafem la velocitat v2
de retrocés del canó quan t
= 0,27 s, en què la velocitat és màxima, am b un
valor de 0,77 m/s,
tal com hem recollit en la taula i podem observar en les gràfiques del
Coach.
El subíndex 2
es refereix al fi de l’explosió i el subíndex 1,
a l’instant abans de l’explosió.
El sistema estudiat és: canó + perdigó.
Velocitat del perdigó
Inicialment està en repòs. Així doncs, p1 = 0 i, per conservació de la quantitat de moviment del sistema,
| M2
v2 + m2 v2 = 0 v2 = -(M2/m2) v2 = -(28,6 / 0,2) 0,77 = - 110,11 m/s = - 396 km/h |
Coeficient de fricció (1)
Per trobar ![]() partirem
del moment en quèV
és màxima. Posteriorment, disminueix i s'aturar per l'acció
de la fricció. Així doncs, V2=
0,77 m/s .
partirem
del moment en quèV
és màxima. Posteriorment, disminueix i s'aturar per l'acció
de la fricció. Així doncs, V2=
0,77 m/s .
V3=
0 perquè s’atura a causa de la fricció, desprès
de recórrer 0,14
m. En la gràfica i en la taula, 0,21
m-0,07 m o,
si en el vídeo, es mesura amb el regle la distància recorreguda
des de l’inici del MRUA fins que s'atura.
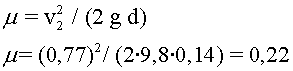
Coeficient de fricció (i 2)
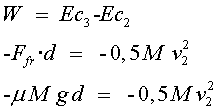
Si s'aïlla, obtenim el mateix valor ![]() .
.
| Sumari |  2/9 2/9  |
| Inici | ||
| ISSN:
1988-7930 Adreça a la xarxa:
www.RRFisica.cat Adreça electrònica:
redaccio@rrfisica.cat
difusio@rrfisica.cat |
||
  Programació web: Xavier Jaén i Daniel Zaragoza. Correcció lingüística: Serveis Linguïstics de la Universitat Politècnica de Catalunya. |
Aquesta
obra està subjecta a una Llicència de Creative Commons |
|
|
Recursos de Física col·labora amb la baldufa i també amb ciències Revista del Professorat de Ciències de Primària i Secundària (Edita: CRECIM-UAB) |
||