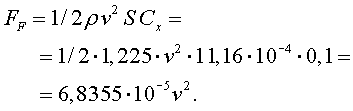
 
Guia del professorat
Estudi de l'equilibri d'una pilota en un brollador
Recordo que a l'escola hi havia uns brolladors on fèiem
ballar les pilotes de ping-pong. Més tard, vaig descobrir que aquesta
era una de les tradicions més singulars de Barcelona. Des del 1637,
el dia de Corpus és costum de fer ballar un ou als brolladors dels
claustres, patis i jardins de la ciutat. Mai no s'ha interromput aquesta
tradició, i l'ou com balla del claustre de la Catedral i
del pati de la Casa de l'Ardiaca són tota una experiència
de primavera viva a la memòria de generacions i generacions de
barcelonins i barcelonines.
Al darrere, hi ha un joc molt senzill, que s'assembla al del brollador
que fa ballar la pilota, que consisteix a mantenir una pilota de ping-pong
flotant a l'aire simplement bufant per un tub. El que jo em pregunto és:
A quina velocitat s'ha de bufar per mantenir la pilota a l'aire?
La pilota no cau perquè l'aire de la bufera la
manté flotant.
La pilota es manté en equilibri (acceleració nul•la)
perquè la suma de totes les forces externes que actuen sobre ella
s'anul•la. Així, la llei de moviment de Newton
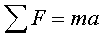 ens diu,
en aquest cas, 
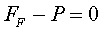, o bé
|
 |
|
 .
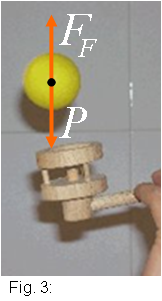
Per tant la força de fricció FF
ha de ser igual però de sentit contrari a la força pes P
.
La força de fricció FF
que fa l'aire sobre la pilota depèn de la densitat de l'aire, de
la seva velocitat, de la forma de l'objecte i de la seva secció,
i ve donada per l'equació:
en què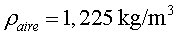 és
la densitat de l'aire, v
és la velocitat de l'aire, S
és la secció del cos que s'oposa al moviment
de l'aire (en aquest cas la pilota) i Cx=0,1
és el coeficient de forma d'una esfera. Per saber-ne
més vegeu les referèmcies de la secció "Enllaços
d'interès"
Tenint en compte que el diàmetre de la pilota és  ,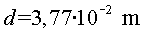
la seva secció serà:
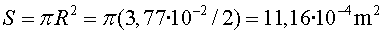
i, per tant, la força de fricció FF
resulta:
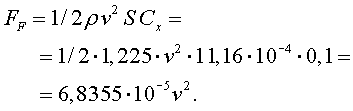
La massa de la pilota és  ,
per la qual cosa així el seu pes és:
Igualant ,
tenim  ,
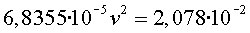i aïllant la velocitat, obtenim:
 .
|
|
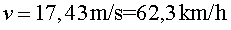Per tant, cal bufar amb una velocitat de 62
km/h per mantenir la pilota de ping-pong en equilibri.
Ara, tornant a la tradicional festa de l'ou com balla, podem preguntar-nos:
Quina hauria de ser la velocitat de l'aigua per mantenir la pilota sobre el
brollador?
|
Respecte als càlculs anteriors, l'únic que canvia
és la densitat. Ara hem de prendre la de l'aigua .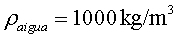
Igualant tenim
ara  ,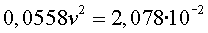
i aïllant la velocitat obtenim:
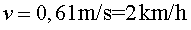
Per tant, l'aigua que està en contacte amb la
pilota ha d'anar a només 2
km/h. En ser la densitat de l'aigua molt més gran que la
de l'aire, la velocitat pot ser molt més petita. |
 |
Proposta didàctica
Amb alumnes de batxillerat, mentre estem estudiant la dinàmica i més
concretament les lleis de Newton, podem dur a terme l'experiència de
la pilota de ping-pong a l'aula (com a element motivador). Posteriorment podem
proposar als alumnes que resolguin a casa les dues qüestions de l'article
donant-los només l'expressió matemàtica (1), que permet
calcular la força de fricció d'un objecte en moviment dins d'un
fluid. Els alumnes hauran d'aplicar la segona llei de Newton i cercar les dades
necessàries per a la resolució matemàtica (mides i massa
de la pilota, densitat de l'aire i de l'aigua).
És molt important que tinguin cura d'utilitzar correctament les unitats
(sovint les densitats les trobem expressades en g/cm3)
i que analitzin la coherència del resultat obtingut.
També els podem demanar que calculin aproximadament la velocitat de l'aigua
de les fonts que aguanten en equilibri els ous en aquesta festa tradicional
barcelonina.
Altres
Segurament, algun alumne es preguntarà perquè
la pilota o l'ou es mantenen en equilibri i no cauen cap als costats. Si cap
alumne ho qüestiona, sempre podem fer nosaltres la pregunta.
Aquesta qüestió seveix per fer alguna experiència molt senzilla
i per parlar força estona sobre l'aerodinàmica. Algunes propostes:
- A més velocita,t la pressió augmenta o disminueix?
- Experiència de bufar fort entre dos fulls de paper.
- Experiència de bufar fort per sobre un full de paper.
- Perquè vola un avió?
- Funcionament de la trompa de buit del laboratori de química ( efecte
Venturi)
Amb tot, per desenvolupar aquest tema caldria tot un altre article.
Enllaços d'interès
| Inici |
|
|
| ISSN:
1988-7930 Adreça a la xarxa:
www.RRFisica.cat Adreça electrònica:
redaccio@rrfisica.cat
difusio@rrfisica.cat
Comitè de redacció : Josep Ametlla, Octavi
Casellas, Xavier Jaén, Gemma Montanyà, Cristina Periago,
Octavi Plana, Jaume Pont i Ramon Sala.
Treballem conjuntament : Societat Catalana de Física,
Associació de Professores i Professors de Física i Química
de Catalunya,XTEC, Universitat Politècnica de Catalunya, Universitat
de Barcelona
|
   
Programació web: Xavier Jaén i Daniel Zaragoza.
Correcció lingüística: Serveis Linguïstics
de la Universitat Politècnica de Catalunya. |
Aquesta
obra està subjecta a una
Llicència
de Creative Commons
|
|
Recursos
de Física col·labora amb la
baldufa i també amb ciències
Revista del Professorat de Ciències de Primària i Secundària
(Edita: CRECIM-UAB)
|
|
|
6/9 
