núm 9 |
Primavera del 2012 |
Societat Catalana de Física |
| Inici |
| Sumari |   7/10 7/10  |
| Reacció (química) i acció (física) Josep Coromines |
|
| S'utilitzen reaccions pròpies de la química per provocar una petita explosió i estudiar, en el terreny de la física, la conservació de la quantitat de moviment. |
IntroduccióEls comprimits efervescents en contacte amb l’aigua generen gas diòxid de carboni per una reacció entre un àcid (àcid cítric o tartàric o un fosfat àcid) i una base (generalment l’hidrogencarbonat de sodi). Si tanquem un comprimit amb una petita quantitat d’aigua dins un pot amb un tap que tanqui a pressió, uns instants després de tapar-lo el tap surt disparat per la pressió del gas que s’hi ha format. Guia per al professoratA la física de batxillerat s’estudia el principi
de conservació de la quantitat de moviment. Els exemples d’aplicació
que normalment es proposen són diversos, però sempre es parla
del retrocés d’un arma en disparar.
|
Una manera de trobar la velocitat del projectil
que dispara un arma és fer impactar el projectil en una massa coneguda
i mesurar la velocitat a què es comença a moure la massa
juntament amb el projectil incrustat.
|
|
| Fig. 2 |
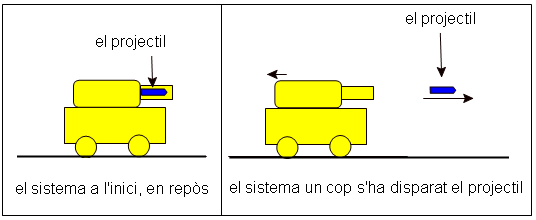
En el nostre cas, per comoditat, el projectil
és el tap d’un envàs. El tap sortirà propulsat
per l’expansió del gas que es genera en la reacció
química que es produeix quan es posa un comprimit efervescent en
aigua.Observeu el muntatge en la figura 3.
|
|
| Fig. 3: |
Un sensor de posició ens permetrà obtenir el gràfic posició-temps del carretó quan retrocedeix.
![]() Si teniu
el gràfic posició-temps del moviment del carretó, com podeu
calcular la velocitat en els primers instants en què el vehicle es comença
a moure?
Si teniu
el gràfic posició-temps del moviment del carretó, com podeu
calcular la velocitat en els primers instants en què el vehicle es comença
a moure?
![]() Escriviu
ara quines magnituds caldrà mesurar per poder fer els càlculs.
Escriviu
ara quines magnituds caldrà mesurar per poder fer els càlculs.
![]() Raoneu
si es conservarà l’energia mecànica del sistema.
Raoneu
si es conservarà l’energia mecànica del sistema.
![]() Un cop
fetes les mesures, expresseu la velocitat a què surt el tap en km/h.
Un cop
fetes les mesures, expresseu la velocitat a què surt el tap en km/h.
![]() En aquest
experiment, el tap i el carretó s’han mogut en la mateixa direcció,
canviarien els resultats si en lloc de sortir el tap en direcció horitzontal,
sortís amb un cert angle respecte de l’horitzontal? Expliqueu-ho.
En aquest
experiment, el tap i el carretó s’han mogut en la mateixa direcció,
canviarien els resultats si en lloc de sortir el tap en direcció horitzontal,
sortís amb un cert angle respecte de l’horitzontal? Expliqueu-ho.
Suposeu que el tap surt sempre a la velocitat que heu calculat.
![]() Per a
les mesures de
Per a
les mesures de ![]() ,
,
![]() i
i ![]() que heu trobat, quina seria la velocitat de retrocés del carretó
si l’angle de sortida del tap fóra de
que heu trobat, quina seria la velocitat de retrocés del carretó
si l’angle de sortida del tap fóra de ![]() ?
?
![]() Podem
considerar el tap com una massa que descriu una trajectòria parabòlica.
Suposant que el fregament amb l’aire és negligible, a quina distància
cauria en un llançament de
Podem
considerar el tap com una massa que descriu una trajectòria parabòlica.
Suposant que el fregament amb l’aire és negligible, a quina distància
cauria en un llançament de ![]() ?
?
|
|
|
| Fig. 4: |
Solucions
![]() Escriviu, per aaquest sistema, l’equació de conservació
de la quantitat de moviment.
Escriviu, per aaquest sistema, l’equació de conservació
de la quantitat de moviment.
![]()
![]() Quines magnituds caldrà mesurar si volem trobar la velocitat a què
surt disparat el projectil?
Quines magnituds caldrà mesurar si volem trobar la velocitat a què
surt disparat el projectil?
Les masses del projectil i del vagó i la velocitat de retrocés del vagó
Un sensor de posició ens permetrà obtenir el gràfic posició-temps del carretó quan retrocedeix.
![]() Si teniu
el gràfic posició-temps del moviment del carretó, com podeu
calcular la velocitat en els primers instants en què el vehicle es comença
a moure?
Si teniu
el gràfic posició-temps del moviment del carretó, com podeu
calcular la velocitat en els primers instants en què el vehicle es comença
a moure?
En el gràfic, caldrà trobar la derivada (el pendent) en els primers instants del moviment.
![]() Escriviu
ara quines magnituds caldrà mesurar per poder fer els càlculs.
Escriviu
ara quines magnituds caldrà mesurar per poder fer els càlculs.
Les masses del tap i del conjunt del vagó amb
el tap, el comprimit i l’aigua.
També haurem d’obtenir el gràfic posició-temps del
moviment o, com a alternativa, mesurar la distància que recorre el carretó
fins que s’atura i el temps que tarda a fer-ho.
![]() Raoneu
si es conservarà l’energia mecànica del sistema.
Raoneu
si es conservarà l’energia mecànica del sistema.
No es conservarà l’energia mecànica perquè hi ha una explosió.
![]() Un cop
fetes les mesures, expresseu la velocitat a què surt el tap en km/h.
Un cop
fetes les mesures, expresseu la velocitat a què surt el tap en km/h.
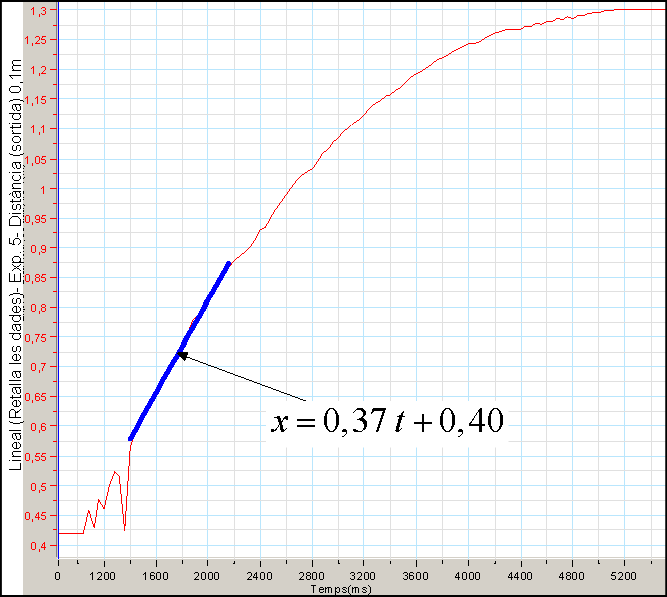
Per a comprimits de la marca Efferalgan, amb ![]() d’aigua, el gràfic que s’obté és:
d’aigua, el gràfic que s’obté és:
| |
| Fig.5: Gràfic |
L’equació de la recta és: ![]() .
Així doncs la velocitat de retrocés és de
.
Així doncs la velocitat de retrocés és de ![]() .
.
Fent el canvi d’unitats, això dóna una velocitat del tap
de ![]() .
.
Aquesta velocitat depèn de molts factors. Caldrà mesurar-la per
a una determinada marca de comprimits efervescents i d’altres factors:
tipus d’envàs…
![]() En aquest
experiment, el tap i el carretó s’han mogut en la mateixa direcció,
canviarien els resultats si en lloc de sortir el tap en direcció horitzontal,
sortís amb un cert angle respecte de l’horitzontal? Expliqueu-ho.
En aquest
experiment, el tap i el carretó s’han mogut en la mateixa direcció,
canviarien els resultats si en lloc de sortir el tap en direcció horitzontal,
sortís amb un cert angle respecte de l’horitzontal? Expliqueu-ho.
La velocitat de retrocés seria inferior.
Suposeu que el tap surt sempre a la velocitat que heu calculat.
![]() Per a
les mesures de
Per a
les mesures de ![]() ,
,
![]() i
i ![]() que heu trobat, quina seria la velocitat de retrocés del carretó
si l’angle de sortida del tap fóra de
que heu trobat, quina seria la velocitat de retrocés del carretó
si l’angle de sortida del tap fóra de ![]() ?
?
La velocitat s’ha de calcular quan es coneixen
les masses MC i mt i s’ha d’agafar el component horitzontal de ![]()
(![]() és el mòdul
de la velocitat inicial del tap)
és el mòdul
de la velocitat inicial del tap)
![]() Podem
considerar el tap com un massa que descriu una trajectòria parabòlica.
Suposant que el fregament amb l’aire és negligible, a quina distància
cauria en un llançament de
Podem
considerar el tap com un massa que descriu una trajectòria parabòlica.
Suposant que el fregament amb l’aire és negligible, a quina distància
cauria en un llançament de ![]() ?
?
Emprant les equacions del moviment parabòlic i
orientant els eixos de coordenades de manera que el punt on cau el tap és![]() :
:
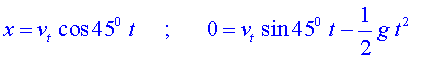
Annex I
|
|
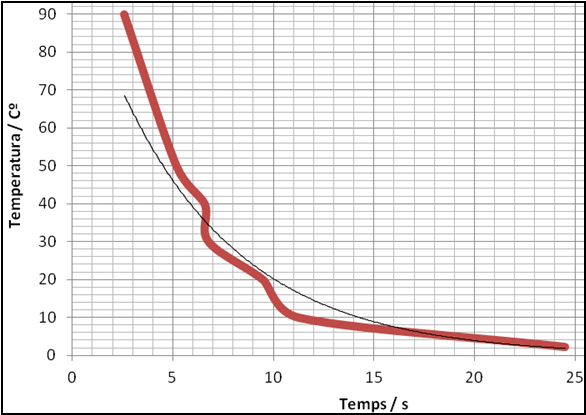
| Fig.6: Gràfic del temps que triga a sortir
disparat el tap d’un envàs de pel•lícula fotogràfica
en funció de la temperatura de l’aigua, per a comprimits de
la marca Efferalgan i amb un volum d’aigua d’ |
Annex II
Les equacions químiques que corresponen a la reacció que genera
el gas ![]() són:
són:
![]() L’àcid cítric
es dissocia en contacte amb l’aigua:
L’àcid cítric
es dissocia en contacte amb l’aigua:
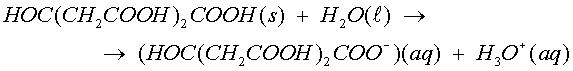
![]() L’hidrogencarbonat de sodi
es dissocia en contacte amb l’aigua:
L’hidrogencarbonat de sodi
es dissocia en contacte amb l’aigua:
![]()
![]() Els ions
Els ions![]() i
i
![]() reaccionen (neutralització)
i es forma el gas diòxid de carboni:
reaccionen (neutralització)
i es forma el gas diòxid de carboni:
![]()
Annex III
Altres possibles muntatges:
|
|
| Fig. 7 |
| A la figura 8, en lloc de la peça FERR PLAST-U32 s’han muntat unes guies d’alumini que permeten subjectar l’envàs de fotos amb l’avantatge que les guies es poden inclinar en diferents angles, tal com es veu en les figures de sota. |
|
| Fig. 8 |
A les figures 9,10 i 11, en lloc de la peça FERR PLAST-U32 s’han muntat unes guies d’alumini que permeten subjectar l’envàs de fotos amb l’avantatge que les guies es poden inclinar en diferents angles.
 |
 |
|
||
| Fig. 9 | Fig. 10 | Fig. 11 |


 ,
una peça de ferreteria que serveix per unir tubs.
,
una peça de ferreteria que serveix per unir tubs. , és un dels millors vehicles que es poden utilitzar.
, és un dels millors vehicles que es poden utilitzar.