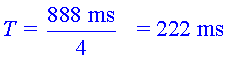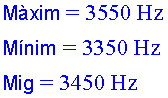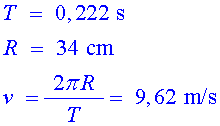núm 11 |
Primavera del 2013 |
Societat Catalana de Física |
| Inici |
| Sumari |   2/9 2/9  |
| Bicidoppler Tavi Casellas, Maria Gubert i Xavier Muñoz |
|
| A les classes de física de batxillerat expliquem l'efecte Doppler ajudant-nos d'algun esquema dels fronts d'ona i posant com a exemple el soroll d'un tren o d'un cotxe quan s'acosta i posteriorment s'allunya, és el típic: iiiiiiaauuuuuuuu. Aquí presentem una experiència que no solament ens permetrà escoltar l'efecte Doppler, sinó que podrem mesurar les freqüències i comprovar que les fórmules teòriques es compleixen (amb els errors experimentals corresponents). Aquesta és una activitat que pot servir de síntesi en finalitzar la unitat d'ones, com a cas pràctic per a l’ús de les noves tecnologies o, fins i tot, pot ser l'embrió d'un treball de recerca. |
A l'aula o a casa l'alumnat ha de fer:
|
Full de l’alumnatObjectiuComprovar, quantitativament, l'efecte Doppler.
Introducció |
|
Fig. 5: |
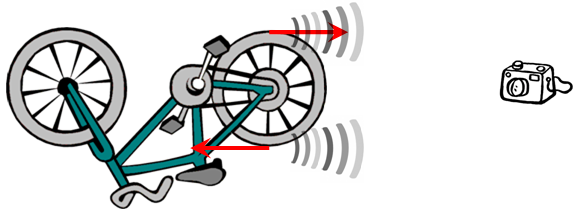
Gravarem un vídeo per poder analitzar-ne el so després
(amb l'Audacity![]() )
i molt especialment la variació de la seva freqüència de
forma periòdica a causa de l'efecte Doppler.
)
i molt especialment la variació de la seva freqüència de
forma periòdica a causa de l'efecte Doppler.
Material
![]() Bicicleta.
Bicicleta.
![]() Brunzidor o mòbil (on es pugui introduir un so generat per l'ordinador).
Brunzidor o mòbil (on es pugui introduir un so generat per l'ordinador).
![]() Càmera fotogràfica o de vídeo.
Càmera fotogràfica o de vídeo.
![]() Cinta mètrica.
Cinta mètrica.
![]() Ordinador amb l'Audacity instal•lat.
Ordinador amb l'Audacity instal•lat.
Realització
![]() Si utilitzeu un mòbil:
Si utilitzeu un mòbil:
- Amb l'Audacity
 ,
genereu un so d'una freqüència determinada (us proposem
,
genereu un so d'una freqüència determinada (us proposem
 ) i exporteu-lo
a format mp3.
) i exporteu-lo
a format mp3.
- Introduïu al mòbil el so generat.
![]() Situeu la bicicleta
cap per avall i enganxeu el brunzidor o el mòbil a la perifèria
de la roda del darrere. Vigileu que en donar voltes l'aparell no toqui el quadre
de la bicicleta i que estigui fixat convenientment per evitar que surti disparat
tangencialment a causa de la velocitat de rotació.
Situeu la bicicleta
cap per avall i enganxeu el brunzidor o el mòbil a la perifèria
de la roda del darrere. Vigileu que en donar voltes l'aparell no toqui el quadre
de la bicicleta i que estigui fixat convenientment per evitar que surti disparat
tangencialment a causa de la velocitat de rotació.
![]() Disposeu un petit
tros de plàstic o cartró en algun punt de la roda que toqui l’estructura
de la bicicleta en passar-hi. D’aquesta manera tindrem un senyal sonor
cada vegada que la roda faci una volta.
Disposeu un petit
tros de plàstic o cartró en algun punt de la roda que toqui l’estructura
de la bicicleta en passar-hi. D’aquesta manera tindrem un senyal sonor
cada vegada que la roda faci una volta.
![]() Mesureu la distància
entre l'eix de la roda i l'altaveu del brunzidor o del mòbil.
Mesureu la distància
entre l'eix de la roda i l'altaveu del brunzidor o del mòbil.
![]() Engegueu el so
i comenceu a pedalar amb la màxima velocitat possible (plat gran i pinyó
petit).
Engegueu el so
i comenceu a pedalar amb la màxima velocitat possible (plat gran i pinyó
petit).
![]() Enregistreu un
vídeo durant uns quants segons des del darrere de la bicicleta, en una
posició perpendicular a l'eix de la roda.
Enregistreu un
vídeo durant uns quants segons des del darrere de la bicicleta, en una
posició perpendicular a l'eix de la roda.
![]() Enregistreu també
un vídeo del brunzidor o del mòbil quan està quiet.
Enregistreu també
un vídeo del brunzidor o del mòbil quan està quiet.
![]() Necessiteu mesurar
el radi de rotació, la distància des de l'eix de la bicicleta
fins l'altaveu del brunzidor o del mòbil.
Necessiteu mesurar
el radi de rotació, la distància des de l'eix de la bicicleta
fins l'altaveu del brunzidor o del mòbil.
Anàlisi i tractament de les dades
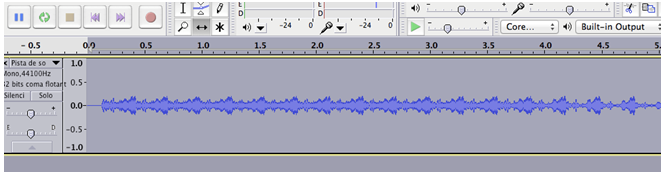
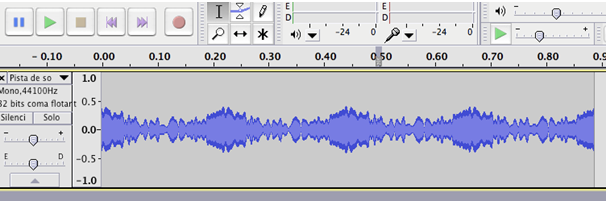
Amb el programari Audacity captureu el so del vídeo:
comenceu la gravació del so intern de l'ordinador i posteriorment engegueu
la reproducció del vídeo.
Elimineu els intervals sonors que no us interessin: inici i final de la gravació.
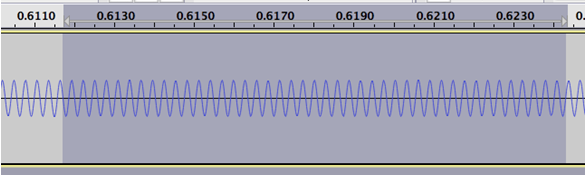
Observeu el so amb detall, augmentant l'eix temporal amb la lupa ![]() ,
per observar les repeticions causades per la rotació.
,
per observar les repeticions causades per la rotació.
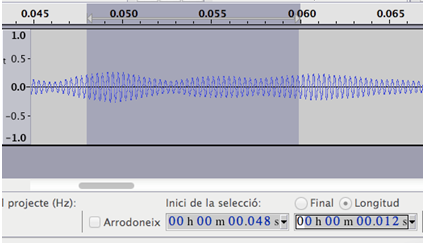
![]() Mesureu aleshores el període de rotació.
Mesureu aleshores el període de rotació.
Retalleu el so corresponent a quatre o cinc períodes de rotació.
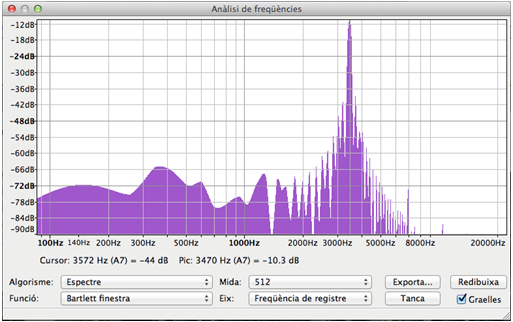
Dividiu els períodes de rotació en una dotzena o quinzena d'intervals
cadascun, aneu-los seleccionant consecutivament i obteniu per a cadascun la
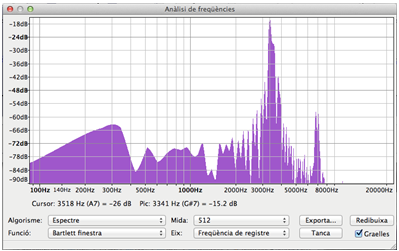
freqüència fonamental del so (en el menú de l'Audacity:
Analitza![]() Traça
l'espectre).
Traça
l'espectre).
Podeu emplenar una taula d'un full de càlcul amb els valors obtinguts,
com ara la taula 1:
| I tot seguit representeu gràficament els valors amb un full de càlcul.
Podeu fer una recerca a Internet per contestar la pregunta següent.
|
|
||||||||||
Taula. 1: |
Ampliació: anàlisi gràfica
|
|
Fig. 6: |
Qüestionari
![]() Podeu explicar
la variació de l'amplitud de l'ona sonora al llarg d'un període?
Podeu explicar
la variació de l'amplitud de l'ona sonora al llarg d'un període?
![]() Relacioneu el moviment del brunzidor amb les dades experimentals.
Relacioneu el moviment del brunzidor amb les dades experimentals.
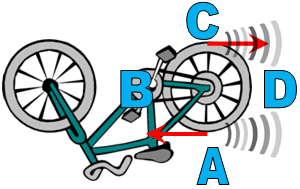
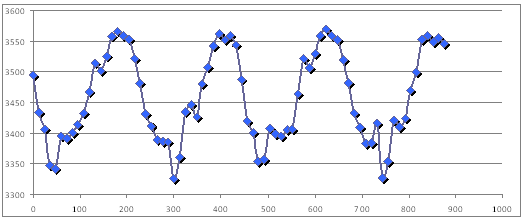
Trieu un període del gràfic experimental i situeu les lletres
A, B,
C i D
en el lloc més probable (vegeu la figura 6).
![]() Què
passaria amb la freqüència si en comptes d’enregistrar el
so alineats amb la bicicleta ho féssim alineats amb l’eix de gir
de la roda?
Què
passaria amb la freqüència si en comptes d’enregistrar el
so alineats amb la bicicleta ho féssim alineats amb l’eix de gir
de la roda?
![]() Podeu proposar
altres experiments per comprovar l'efecte Doppler?
Podeu proposar
altres experiments per comprovar l'efecte Doppler?
![]() Citeu algunes
aplicacions que té l'efecte Doppler en la vida quotidiana.
Citeu algunes
aplicacions que té l'efecte Doppler en la vida quotidiana.
Solucions
| Amb el programari Audacity |
|
Fig. 7 |
| Retalleu el so corresponent a quatre o cinc períodes de rotació.
888
ms correspon a 4
períodes |
|
Fig. 8 |
Dividiu els períodes de rotació en una dotzena
o quinzena d'intervals cadascun, aneu-los seleccionant consecutivament i obteniu
per a cadascun la freqüència fonamental del so (Analitza![]() Traça l'espectre).
Traça l'espectre).
|
|
|
| Fig. 9 | Fig. 10 |
| Podeu oemplenar una taula d'un full de càlcul amb els valors obtinguts com ara: I tot seguit representeu gràficament els valors amb un full de càlcul.
|
|
||||||||||||||||||||||||||
Taula 2 |
|
|
|
Fig. 12 |
|
|
|
Fig. 13 |
Podeu fer una cerca a Internet per contestar la pregunta següent.
![]() La fórmula
que permet calcular les variacions de freqüències per l'efecte Doppler
és:
La fórmula
que permet calcular les variacions de freqüències per l'efecte Doppler
és:
La fórmula és extreta de
la Wikipedia en castellà: http://es.wikipedia.org/wiki/Efecto_Doppler
![]()
![]() :
velocitat del so,
:
velocitat del so, ![]() :
velocitat de l'observador (zero en el nostre cas),
:
velocitat de l'observador (zero en el nostre cas), ![]() :
velocitat de l'emissor,
:
velocitat de l'emissor, ![]() :
freqüència de l'emissor en repòs,
:
freqüència de l'emissor en repòs, ![]() : freqüència aparent observada
: freqüència aparent observada
Calculeu ara les freqüències teòriques esperades en el punt
de màxima velocitat d'apropament i d'allunyament del brunzidor o del
mòbil.
![]() Freqüència
quan s'allunya:
Freqüència
quan s'allunya:
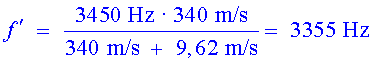
![]() Freqüència
quan s'acosta:
Freqüència
quan s'acosta:
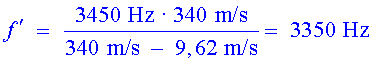
![]() Feu un
comentari global sobre els valors obtinguts i els valors esperats.
Feu un
comentari global sobre els valors obtinguts i els valors esperats.
Els resultats obtinguts experimentalment (de forma gràfica
i aproximada) concorden de manera sorprenent amb la predicció teòrica.
Ampliació: anàlisi gràfica
Podeu fer un pas més en l'experiència: buscar la funció
matemàtica que més s'ajusti als valors experimentals per comprovar-ne
la validesa.
Per fer-ho podeu utilitzar el programari CurveExpert Basic 1.4 (versió
d'avaluació) que permet obtenir una regressió sinusoïdal
d'un conjunt de valors (com és el nostre cas). Podeu obtenir-lo a:
Abans de fer-ho cal que, amb el full
de càlcul, calculeu la mitjana de les freqüències obtingudes
i obtingueu una nova columna amb la desviació de les freqüències
respecte d'aquesta mitjana.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Taula. 3 |
En el programa CurveExpert Basic introduïu els valors de temps i de les desviacions.
 |
Fig. 14 |
Realitzeu seguidament l'anàlisi Apply Fit ![]() Miscellaneous
Miscellaneous
![]() Sinusoidal...
Sinusoidal...
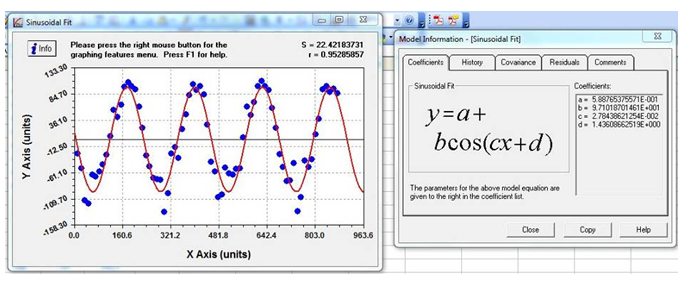 |
Fig. 15 |
![]() Comenteu la funció obtinguda a partir de les dades experimentals i la
seva relació amb les dades teòriques.
Comenteu la funció obtinguda a partir de les dades experimentals i la
seva relació amb les dades teòriques.
![]()
Si tornem a sumar-hi la mitjana obtenim
![]()
Així doncs el valor màxim (el brunzidor s'acosta) de freqüència
seria
![]()
I el valor mínim (el brunzidor s'allunya)
![]()
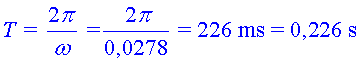
Dades que també concorden molt amb els valors esperats
![]() Calculeu
l'error absolut i relatiu de les freqüències obtingudes.
Calculeu
l'error absolut i relatiu de les freqüències obtingudes.
Freqüència màxima:
![]()
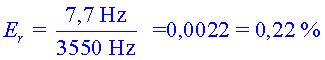
Freqüència mínima:
![]()
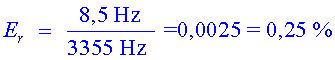
Qüestionari
![]() Podeu explicar
la variació de l'amplitud de l'ona sonora al llarg d'un període?
Podeu explicar
la variació de l'amplitud de l'ona sonora al llarg d'un període?
L'amplitud varia per diferents motius. D’una banda,
a causa de la variació de la distància respecte de la càmera
i, de l’altra, a causa de les interferències del so amb les reflexions
que fa mateix en l'estructura de la bicicleta i en els objectes propers (parets,
terra...).
![]() Relacioneu
el moviment del brunzidor amb les dades experimentals.
Relacioneu
el moviment del brunzidor amb les dades experimentals.
Trieu un període del gràfic experimental i situeu les lletres
A, B,
C i D
en el lloc més probable.
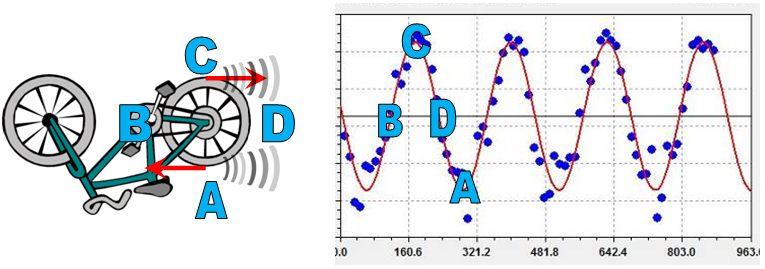 |
Fig. 16 |
La freqüència més
alta s’aconsegueix quan la component x
de la velocitat del brunzidor té un valor positiu i és més
gran: posició C,
que correspon a la cresta del gràfic.
La freqüència més baixa s’aconsegueix quan la component
x de la
velocitat del brunzidor té un valor negatiu i és més gran:
posició A, que
correspon a la vall del gràfic.
![]() Què
passaria amb la freqüència si en comptes d’enregistrar el
so alineats amb la bicicleta ho féssim alineats amb l’eix de gir
de la roda?
Què
passaria amb la freqüència si en comptes d’enregistrar el
so alineats amb la bicicleta ho féssim alineats amb l’eix de gir
de la roda?
Si ens situem alineats amb l’eix, el brunzidor pràcticament
no s’allunya ni s’acosta i, en aquest cas, no es produeix l’efecte
Doppler. La freqüència no variaria.
![]() Podeu proposar
altres experiments per comprovar l'efecte Doppler?
Podeu proposar
altres experiments per comprovar l'efecte Doppler?
Es podria realitzar amb l'ajut d'un cotxe que circulés
a una velocitat constant en una carretera recta mentre toca el clàxon.
Una persona hauria de gravar el cotxe mentre s'apropa i s'allunya. Dins del
cotxe una persona ha de mesurar la velocitat amb l'ajut d'un navegador amb GPS
o d'un telèfon intel•ligent amb una aplicació adequada (el
velocímetre dels cotxes sempre tenen errors importants).
Una altra experiència que pot ser interessant: deixar oscil•lar
(moviment harmònic) el brunzidor lligat a una molla llarga.
I encara una tercera: deixar caure lliurement el brunzidor durant alguns segons
des d'un segon o tercer pis, capturant el so des de dalt i des de baix. Cal
preveure la possibilitat que el brunzidor en acabar deixi de funcionar!
![]() Esmenteu
algunes aplicacions que té l'efecte Doppler en la vida quotidiana.
Esmenteu
algunes aplicacions que té l'efecte Doppler en la vida quotidiana.
El radar, les ecocardiografies, mesures de distàncies
en astrofísica, els ratpenats per evitar col•lisionar...